38 câu hỏi trắc nghiệm thuộc Bộ 20 đề thi giữa học kì 1 Toán 11 năm 2022 - 2023 có đáp án (Đề 1)

Câu 1:

Tập xác định của hàm số $y = \tan x$ là

A. $D = ℝ \ \{\frac{π}{2} + k π, k \in ℤ\} .$

B.

D = ℝ \ \{k π, k \in ℤ\} .

C.

D = ℝ .

D.

D = ℝ \ \{\frac{π}{2} + k 2 π, k \in ℤ\} .

Xem đáp án

Chọn A

Hàm số y = tan xcó tập xác định là $D = ℝ \ \{\frac{π}{2} + k π, k \in ℤ\} .$

Câu 2:

Tập giá trị của hàm số

y = \cos 2 x

là

A. R

B.

[- 1; 1] .

C.

[- 2; 2] .

D.

(0; + \infty) .

Xem đáp án

Chọn B

Vì $\forall x \in ℝ : - 1 \leq \cos 2 x \leq 1$ nên tập giá trị của hàm số y = cos 2xlà $[- 1; 1] .$

Câu 3:

Chu kì tuần hoàn của hàm số

y = \cot x

là

A.

T = k π, k \in ℤ .

B.

T = 2 π .

C.

T = π .

D.

T = \frac{π}{2} .

Xem đáp án

Chọn C

Câu 4:

Hàm số

y = \sin x

có chu kì tuần hoàn là

A.

π .

B.

3 π .

C.

2 π .

D.

\frac{π}{2} .

Xem đáp án

Chọn C

Lý thuyết sách giáo khoa.

Câu 5:

Cho đồ thị

Hàm số nào dưới đây có đồ thị là hình trên

A.

y = \sin x .

B.

y = \cos x .

C.

y = \tan x .

D.

y = \cot x .

Xem đáp án

Chọn D

Lý thuyết sách giáo khoa.

Câu 6:

Phương trình

s inx = \sin α

(đơn vị của

α

là radian) có nghiệm là:

A. $[\begin{array}{l} x = α + k 2 π \\ x = π - α + k 2 π \end{array}, k \in Z .$

B.

[\begin{array}{l} x = α + k 2 π \\ x = - α + k 2 π \end{array}, k \in Z .

C.

[\begin{array}{l} x = α + k π \\ x = π - α + k π \end{array}, k \in Z .

D.

[\begin{array}{l} x = α + k π \\ x = - α + k π \end{array}, k \in Z .

Xem đáp án

Chọn A

Lý thuyết sách giáo khoa.

Câu 7:

Phương trình

\tan x = \tan α

với

α

là một số cho trước có các nghiệm là gì?

A. $[\begin{array}{l} x = α + k 2 π \\ x = - α + k 2 π \end{array}, k \in ℤ .$

B.

[\begin{array}{l} x = α + k 2 π \\ x = - α + k 2 π \end{array}, k \in ℤ .

C.

x = α + k 2 π, k \in ℤ .

D.

x = α + k π, k \in ℤ .

Xem đáp án

Chọn D

Ta có: $\tan x = \tan α \Leftrightarrow x = α + k π, k \in ℤ .$

Câu 8:

Tìm nghiệm của phương trình

\cos x = \frac{1}{2} .

A. $[\begin{array}{l} x = \frac{π}{3} + k 2 π \\ x = - \frac{π}{3} + k 2 π \end{array}, k \in ℤ .$

B.

[\begin{array}{l} x = \frac{π}{6} + k π \\ x = - \frac{π}{6} + k π \end{array}, k \in ℤ .

C.

[\begin{array}{l} x = \frac{π}{6} + k 2 π \\ x = - \frac{π}{6} + k 2 π \end{array}, k \in ℤ .

D.

[\begin{array}{l} x = \frac{π}{3} + k π \\ x = - \frac{π}{3} + k π \end{array}, k \in ℤ .

Xem đáp án

Chọn A

Ta có: $\cos x = \frac{1}{2} \Leftrightarrow \cos x = \cos \frac{π}{3} \Leftrightarrow [\begin{array}{l} x = \frac{π}{3} + k 2 π \\ x = - \frac{π}{3} + k 2 π \end{array}, k \in ℤ .$

Câu 9:

Tìm nghiệm của phương trình

\cot x = \sqrt{3} .

A.

x = \frac{π}{6} + k 2 π, k \in ℤ .

B.

x = \frac{π}{6} + k π, k \in ℤ .

C.

x = \frac{π}{3} + k 2 π, k \in ℤ .

D.

x = \frac{π}{3} + k π, k \in ℤ .

Xem đáp án

Chọn B

Ta có: $\cot x = \sqrt{3} \Leftrightarrow \cot x = \cot \frac{π}{6} \Leftrightarrow x = \frac{π}{6} + k π, k \in ℤ .$

Câu 10:

Trong các phương trình sau phương trình nào là phương trình bậc nhất đối với hàm số y = sin x

A.

2 \cos x - 1 = 0

.

B.

3 \sin x + 4 = 0

.

C.

\sqrt{3} \tan x - 1 = 0

.

D.

2 \sin 3 x + 1 = 0

.

Xem đáp án

Chọn B

Câu 11:

Một tổ có 4 học sinh nữ và 7 học sinh nam. Hỏi có bao nhiêu cách chọn ngẫu nhiên một học sinh của tổ đó đi trực nhật.

A. 20

B. 11

C. 30

D. 10

Xem đáp án

Chọn B

Chọn ngẫu nhiên một học sinh từ 11 học sinh, ta có 11 cách chọn.

Câu 12:

Một người vào cửa hàng ăn, người đó chọn thực đơn gồm 1 món ăn trong 5 món ăn, 1 loại quả tráng miệng trong 4 loại quả tráng

miệng và 1 loại nước uống trong 3loại nước uống. Hỏi có bao nhiêu cách chọn thực đơn?

A. 75

B. 12

C. 60

D. 3

Xem đáp án

Chọn C

Có 5 cách chọn 1 món ăn trong 5 món ăn

4 cách chọn 1 loại quả tráng miệng trong 4 loại quả tráng miệng

3 cách chọn 1 loại nước uống trong 3 loại nước uống.

Theo quy tắc nhân có $5.4.3 = 60$ cách chọn thực đơn.

Câu 13:

Số cách sắp xếp 10 học sinh thành một hàng dọc

A.

10! .

B. 10

C.

C_{10}^{1} .

D.

A_{10}^{1} .

Xem đáp án

Chọn A

Mỗi cách sắp xếp 10 học sinh thành một hàng dọc là một hoán vị của 10 phần tử.

Vậy số cách sắp xếp là: $P_{10} = 10! .$

Câu 14:

Với n là số nguyên dương tùy ý,

n \geq 4

. Mệnh đề nào sau đây đúng?

A. $A_{n}^{4} = \frac{n!}{(n - 4)!} .$

B.

A_{n}^{4} = \frac{n!}{(n - 4)! 4!}

.

C.

A_{n}^{4} = \frac{4. n!}{(n - 4)!}

.

D.

A_{n}^{4} = \frac{4! n!}{(n - 4)!} .

Xem đáp án

Chọn A

Công thức chỉnh hợp chập k của n phần tử.

Câu 15:

Cho tập A gồm n phần tử,

n \geq 1

. Số tập con gồm k phần tử của tập A được xác định bởi công thức

A. $C_{n}^{k} = \frac{n!}{(n - k)! k!} .$

B.

A_{n}^{k} = \frac{n!}{(n - k)!} .

C.

A_{n}^{k} = \frac{n!}{(n - k)! k!}

D.

C_{n}^{k} = \frac{k! n!}{(n - k)!} .

Xem đáp án

Chọn A

Công thức tổ hợp chập k của n phần tử.

Câu 16:

Cho điểm

A' (1; 4)

và

\vec{u} = (- 2; 3),

biết A' là ảnh của A qua phép tịnh tiến theo

\vec{u} .

Tìm tọa độ điểm A

A.

A (1; 4) .

B.

A (- 3; - 1) .

C.

A (- 1; - 4) .

D.

A (3; 1) .

Xem đáp án

Chọn D

Gọi A(x;y)Ta có: $\vec{A A'} = \vec{u} \Leftrightarrow \{\begin{cases} 1 - x = - 2 \\ 4 - y = 3 \end{cases} \Leftrightarrow \{\begin{cases} x = 3 \\ y = 1 \end{cases} \Rightarrow A (3; 1)$

Câu 17:

Mệnh đề nào sau đây là sai?

A. Phép đối xứng trục bảo toàn khoảng cách giữa hai điểm bất kì.

B. Phép đối xứng trục biến một đường thẳng thành một đường thẳng song song hoặc trùng với đường thẳng đã cho.

C. Phép đối xứng trục biến tam giác thành tam giác bằng tam giác đã cho.

D. Phép đối xứng trục biến đường tròn thành đường tròn bằng đường tròn đã cho.

Xem đáp án

Chọn B

Phép đối xứng trục biến đường thẳng thành đường thẳng có thể cắt nhau.

Câu 18:

Cho lục giác đều ABCDEF tâm O. Tìm ảnh của tam giác ABD qua phép đối xứng tâm tâm O

A.

Δ A D B .

B.

Δ D E A .

C.

Δ D C F .

D.

Δ E A D .

Xem đáp án

Chọn D

Phép đối xứng tâm O biến điểm A thành điểm D

Phép đối xứng tâm O biến điểm B thành điểm E

Phép đối xứng tâm O biến điểm D thành điểm A

Vậy ảnh của tam giác ABD qua phép đối xúng tâm O là tam giác DEA

Câu 19:

Phép quay tâm O góc

α

biến điểm M thành điểm M'. Khi đó:

A. $O M^{'} = O M$ .

B.

\vec{O M^{'}} = \vec{O M}

.

C.

\vec{O M^{'}} = \vec{- O M}

.

D.

O M^{'} \neq O M

.

Xem đáp án

Chọn A

Câu 20:

Phép vị tự tỉ số k

(k \in ℝ)

biến một đường tròn có bán kính R = 2 thành đường tròn có bán kính là:

A. $2 |k|$ .

B. 2k.

C. 4k.

D.

4 |k|

.

Xem đáp án

Chọn A

Phép vị tự tỉ số k biến một đường tròn có bán kính R = 2 thành đường tròn có bán kính $|k| R = 2 |k|$ .

Câu 21:

Hàm số y = sin x đồng biến trên khoảng nào dưới đây:

A. $(\frac{π}{2}; \frac{3 π}{2})$ .

B.

(π; 2 π)

.

C.

(- \frac{π}{2}; \frac{π}{2})

.

D.

(0; π)

.

Xem đáp án

Chọn C

Hàm số y = sin x đồng biến trên $(- \frac{π}{2} + k 2 π; \frac{π}{2} + k 2 π), k \in ℤ$ .

Do đó hàm số đồng biến trên $(- \frac{π}{2}; \frac{π}{2})$ .

Câu 22:

Có bao nhiêu giá trị nguyên của tham số m để phương trình

\cos (2 x - \frac{π}{3}) - m = 2

có nghiệm ?

A. 1

B. 2

C. 3

D. 4

Xem đáp án

Chọn C

Câu 23:

Có bao nhiêu giá trị nguyên của tham số m thuộc khoảng (-10;10) để phương trình sin x = m - 4vô nghiệm ?

A. 15

B. 16

C. 17

D. 18

Xem đáp án

Chọn B

Ta có phương trình sin x = m - 4 vô nghiệm khi $[\begin{array}{l} m - 4 > 1 \\ m - 4 < - 1 \end{array} \Leftrightarrow [\begin{array}{l} m > 5 \\ m < 3 \end{array} .$

Vì $m \in (- 10; 10)$ nên $m \in \{- 9; - 8; - 7; - 6; - 5; - 4; - 3; - 2; - 1; 0; 1; 2; 6; 7; 8; 9\}$

Vậy có 16 giá trị m cần tìm.

Câu 24:

Phương trình lượng giác

2 \cos x + \sqrt{2} = 0

có nghiệm là:

A.

[\begin{array}{l} x = \frac{π}{4} + k 2 π \\ x = \frac{3 π}{4} + k 2 π \end{array}

B.

[\begin{array}{l} x = \frac{3 π}{4} + k 2 π \\ x = \frac{- 3 π}{4} + k 2 π \end{array}

C.

[\begin{array}{l} x = \frac{5 π}{4} + k 2 π \\ x = \frac{- 5 π}{4} + k 2 π \end{array}

D.

[\begin{array}{l} x = \frac{π}{4} + k 2 π \\ x = \frac{- π}{4} + k 2 π \end{array}

.

Xem đáp án

Chọn B

$2 \cos x + \sqrt{2} = 0 \Leftrightarrow \cos x = - \frac{\sqrt{2}}{2} \Leftrightarrow \cos x = \cos \frac{3 π}{4} \Leftrightarrow [\begin{array}{l} x = \frac{3 π}{4} + k 2 π \\ x = - \frac{3 π}{4} + k 2 π \end{array}, (k \in ℤ)$ .

Câu 25:

Tất cả các nghiệm của phương trình

\cot^{2} x - \sqrt{3} \cot x = 0

là?

A. $x = \frac{π}{2} + k π, x = \frac{π}{3} + k π, k \in Ζ .$

B.

x = k π, x = \frac{π}{3} + k π, k \in Ζ .

C.

x = \frac{π}{2} + k π, x = \frac{π}{6} + k π, k \in Ζ .

D.

x = k π, x = \frac{π}{6} + k π, k \in Ζ .

Xem đáp án

Chọn C

$\cot^{2} x - \sqrt{3} \cot x = 0 \Leftrightarrow [\begin{array}{l} \cot x = 0 \\ \cot x = \sqrt{3} \end{array} \Leftrightarrow [\begin{array}{l} x = \frac{π}{2} + k π \\ x = \frac{π}{6} + k π \end{array}, k \in Ζ$

Vậy chọn đáp án C.

Câu 26:

Số nghiệm của phương trình

\sin x + \cos x = - \sqrt{2}

trên đoạn

[- \frac{π}{2}; π]

là?

A. 3

B. 2

C. 1

D. 0

Xem đáp án

Chọn D

Câu 27:

Xét mạng đường nối các tỉnh A,B,C,D trong đó số viết trên mỗi cạnh cho biết số con đường nối hai tỉnh nằm ở hai đầu mút của cạnh( hình vẽ sau). Hỏi có bao nhiêu cách đi từ tỉnh A đến tỉnh D

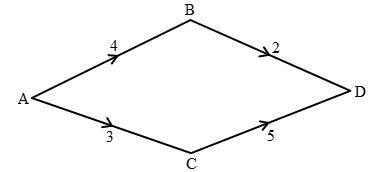
Xét mạng đường nối các tỉnh A,B,C,D trong đó số viết trên mỗi cạnh cho biết số con đường nối hai tỉnh nằm ở (ảnh 1)

A. 14

B. 23

C. 120

D. 48

Xem đáp án

Chọn B

Để đi từ tỉnh A đến tỉnh D có hai hướng là hướng 1 từ A qua B đến D hoặc hướng 2 từ A qua C đến D. Trong đó theo hướng 1, ta có với mỗi cách đi từ A đến B thì có 2 đường đi từ B đến D mà từ A đến B có 4 đường đi nên có $4.2 = 8$ cách đi theo hướng 1. Theo hướng 2, ta có với mỗi cách đi từ A đến C thì có 55 đường đi từ C đến D mà từ A đến C có 3 đường đi nên có $3.5 = 15$ cách đi theo hướng 2. Do đó số cách đi từ tỉnh A đến tỉnh D là $8 + 15 = 23$ cách. Vậy chọn đáp án B.

Câu 28:

Có 10 quả cầu đỏ được đánh số từ 1 đến 10, 7 quả cầu xanh được đánh số từ 1 đến 7 và 8 quả cầu vàng được đánh số từ 1 đến 8. Hỏi có bao nhiêu cách lấy ra 3 quả cầu khác màu và khác số.

A. 22

B. 1540

C. 9240

D. 392

Xem đáp án

Chọn D

Ta chọn các quả cầu theo trình tự sau:

Chọn quả xanh: 7 cách chọn.

Chọn quả cầu vàng: có 7 cách chọn.

Chọn quả cầu đỏ: có 8 cách chọn.

Vậy có tất cả $7.7.8 = 392$ cách chọn.

Câu 29:

Có bao nhiêu cách xếp 5 sách Văn khác nhau và 7 sách Toán khác nhau trên một kệ sách dài nếu các sách Văn phải xếp kề nhau?

A. $5! .7!$ .

B.

2 . 5! .7!

.

C.

5! . 8!

.

D.

12!

.

Xem đáp án

Chọn C

Sắp 5 quyển văn có $5!$ cách sắp xếp.

Sắp 7 quyển toán và bộ 5 quyển văn có $8!$ cách sắp xếp.

Vậy có $5! .8!$ cách sắp xếp.

Câu 30:

Một tổ có 6 học sịnh nam và 9 học sinh nữ. Hỏi có bao nhiêu cách chọn 6 học sinh đi lao động, trong đó có đúng 2 học sinh nam?

A.

C_{6}^{2} + C_{9}^{4}

.

B.

C_{6}^{2} C_{13}^{4}

.

C.

A_{6}^{2} A_{9}^{4}

.

D.

C_{6}^{2} C_{9}^{4}

.

Xem đáp án

Chọn D

Chọn 2 học sinh nam, có $C_{6}^{2}$ cách.

Chọn 4 học sinh nữ, có $C_{9}^{4}$ cách.

Vậy có $C_{6}^{2} C_{9}^{4}$ cách chọn thỏa yêu cầu bài toán.

Câu 31:

Trong mặt phẳng Oxy cho

\vec{v} = (- 2; 3)

và đường thẳng d: 3x - 5y + 3 = 0 ảnh của d qua phép tịnh tiến theo

\vec{v}

có phương trình là:

A.

5 x - 3 y + 5 = 0.

B.

5 x + 3 y - 5 = 0.

C.

3 x - 5 y + 24 = 0.

D.

3 x - 5 y - 3 = 0.

Xem đáp án

Chọn C

Câu 32:

Trong mặt phẳng Oxy cho điểm A(2;5). Hỏi A là ảnh của điểm nào trong các điểm sau qua phép đối xứng trục Ox?

A. (-2;5)

B. (5;-2)

C. (-2;5)

D. (2;-5)

Xem đáp án

Chọn D

Gọi B(x;y) là điểm sao cho $A = Ð_{O x} (B)$ . Khi đó:

$\{\begin{cases} 2 = x \\ 5 = - y \end{cases} \Leftrightarrow \{\begin{cases} x = 2 \\ y = - 5 \end{cases} \Rightarrow B (2; - 5) .$

Câu 33:

Trong mặt phẳng Oxy cho đường tròn (C) có phương trình

{(x - 1)}^{2} + {(y - 2)}^{2} = 4.

Phép đối xứng tâm I(-1;3) biến (C) thành đường tròn nào trong các đường tròn có phương trình sau?

A. ${(x + 5)}^{2} + {(y + 5)}^{2} = 4.$

B.

{(x + 5)}^{2} + {(y + 5)}^{2} = 16.

C.

{(x + 5)}^{2} + {(y - 5)}^{2} = 16.

D.

{(x + 3)}^{2} + {(y - 4)}^{2} = 4.

Xem đáp án

Chọn D

Câu 34:

Cho lục giác đều ABCDEF tâm O như hình vẽ.

Xác định ảnh của cạnh AB qua phép quay tâm O góc quay 120

°

A. $Q_{(O {,120}^{0})} (A B) = B C .$

B.

Q_{(O {,120}^{0})} (A B) = F A .

C.

Q_{(O {,120}^{0})} (A B) = C D .

D.

Q_{(O {,120}^{0})} (A B) = E F

Xem đáp án

Chọn D

Theo định nghĩa, góc quay 120 $°$ có chiều quay ngược chiều quay của kim đồng hồ.

Dựa vào hình vẽ ta có đáp án.

Câu 35:

Trong mặt phẳng tọa độ Oxy, cho điểm M(2;3)Tìm tọa độ ảnh M'của M qua phép vị tự tâm O tỷ số 2.

A. $M^{'} (1; \frac{3}{2}) .$

B.

M^{'} (2; 6) .

C.

M^{'} (4; 3) .

D.

M^{'} (4; 6) .

Xem đáp án

Chọn D

Gọi M'(x';y') là ảnh của M qua phép vị tự tâm O tỷ số 2, theo định nghĩa ta có:

$\vec{O M^{'}} = 2 \vec{O M} \Leftrightarrow \{\begin{cases} x^{'} = 2.2 = 4 \\ y^{'} = 2.3 = 6 \end{cases}$

Vậy M'(4;6)

Câu 36:

Giải phương trình: $\cos x - 2 \cos 2 x + \sqrt{3} \sin x = 0$ .

Xem đáp án

Ta có: $\cos x - 2 \cos 2 x + \sqrt{3} \sin x = 0 \Leftrightarrow \cos x + \sqrt{3} \sin x = 2 \cos 2 x$ $\Leftrightarrow \frac{1}{2} \cos x + \frac{\sqrt{3}}{2} \sin x = \cos 2 x$ $\Leftrightarrow \cos (x - \frac{π}{3}) = \cos 2 x$ $\Leftrightarrow [\begin{array}{l} 2 x = x - \frac{π}{3} + k 2 π \\ 2 x = - x + \frac{π}{3} + k 2 π \end{array}$ $\Leftrightarrow [\begin{array}{l} x = - \frac{π}{3} + k 2 π \\ x = \frac{π}{9} + \frac{k 2 π}{3} \end{array}, k \in ℤ$ .

Câu 37:

Trong hệ Oxy, cho hai điểm A(-1;1);B(1;2) và đường tròn $(C) : x^{2} + y^{2} - 2 x + 4 y = 0$ . Hãy tìm phương trình đường tròn (C') là ảnh của đường tròn (C) qua phép tịnh tiến theo véctơ $\vec{A B}$ .

Xem đáp án

Ta có: $\vec{A B} = (2; 1)$ . Đường tròn (C) có tâm I( 1;-2) và bán kính $R = \sqrt{5}$ , suy ra đường tròn (C') có bán kính $R^{'} = R = \sqrt{5}$ .

Giả sử đường tròn (C') có tâm $I^{'} \Rightarrow T_{\vec{A B}} (I) = I^{'}$ $\Leftrightarrow \vec{I I^{'}} = \vec{A B} \Rightarrow I^{'} (3; - 1)$ .

Vậy phương trình đường tròn (C') là: ${(x - 3)}^{2} + {(y + 1)}^{2} = 5$ .

Câu 38:

Tìm số tự nhiên n thỏa mãn $\frac{C_{n}^{0}}{1.2} + \frac{C_{n}^{1}}{2.3} + \frac{C_{n}^{2}}{3.4} + ... + \frac{C_{n}^{n}}{(n + 1) (n + 2)} = \frac{2^{100} - n - 3}{(n + 1) (n + 2)}$ .

Xem đáp án

$\frac{C_{n}^{k}}{(k + 1) (k + 2)} = \frac{n!}{k! (n - k)! (k + 1) (k + 2)} = \frac{(n + 2)!}{(n - k)! (k + 2)! (n + 1) (n + 2)} = \frac{C_{n + 2}^{k + 2}}{(n + 1) (n + 2)}$ .

Suy ra: $\sum_{k = 0}^{n} \frac{C_{n}^{k}}{(k + 1) (k + 2)} = \sum_{k = 0}^{n} \frac{C_{n + 2}^{k + 2}}{(n + 1) (n + 2)}$

$\Leftrightarrow \frac{C_{n}^{0}}{1.2} + \frac{C_{n}^{1}}{2.3} + \frac{C_{n}^{2}}{3.4} + ... + \frac{C_{n}^{n}}{(n + 1) (n + 2)} = \frac{C_{n + 2}^{2} + C_{n + 2}^{3} + C_{n + 2}^{4} + ... + C_{n + 2}^{n + 2}}{(n + 1) (n + 2)}$ $(*)$ .

Ta xét khai triển sau: ${(1 + x)}^{n + 2} = C_{n + 2}^{0} + x . C_{n + 2}^{1} + x^{2} . C_{n + 2}^{2} + x^{3} . C_{n + 2}^{3} + ... + x^{n + 2} . C_{n + 2}^{n + 2}$ .

Chọn $x = 1 \overset{}{\to} 2^{n + 2} = C_{n + 2}^{0} + C_{n + 2}^{1} + C_{n + 2}^{2} + C_{n + 2}^{3} + ... + C_{n + 2}^{n + 2}$ .

Do đó: $(*) \Leftrightarrow \frac{2^{100} - n - 3}{(n + 1) (n + 2)} = \frac{2^{n + 2} - C_{n + 2}^{0} - C_{n + 2}^{1}}{(n + 1) (n + 2)} \Leftrightarrow 2^{100} = 2^{n + 2} \Leftrightarrow n = 98$ .