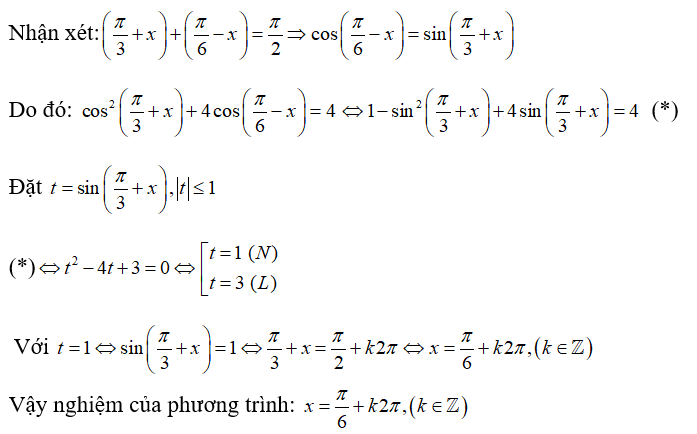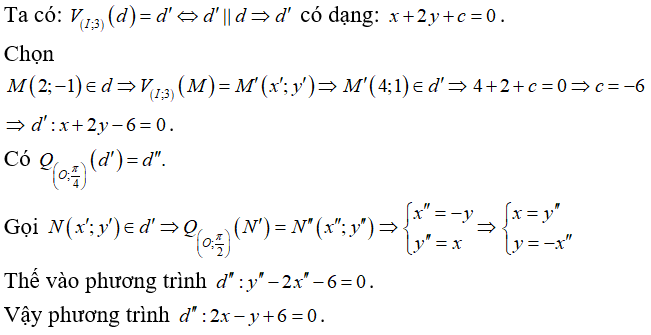39 câu hỏi trắc nghiệm thuộc Bộ 20 đề thi giữa học kì 1 Toán 11 năm 2022 - 2023 có đáp án (Đề 17)

Câu 1:

Tập xác định của hàm số y = 2 + 3tanx là

A. $D = ℝ \ \{\frac{π}{3} + k π\}$ .

B.

D = ℝ \ \{\frac{π}{6} + k π\}

.

C.

D = ℝ \ \{\frac{π}{2} + k π\}

.

D.

D = ℝ \ \{\frac{π}{4} + k π\}

.

Xem đáp án

Chọn C

ĐKXĐ $\cos x \neq 0 \Leftrightarrow x \neq \frac{π}{2} + k π$ . Do đó tập xác định của hàm số là $D = ℝ \ \{\frac{π}{2} + k π\}$ .

Câu 2:

Giá trị nhỏ nhất của hàm số y = 5 - 3cosx bằng

A. 5

B. 4

C. 2

D. -3

Xem đáp án

Chọn C

Câu 3:

Hàm số nào sau đâu có đồ thị nhận trục tung làm trục đối xứng?

A. $y = \frac{\sin x}{x}$ .

B. y = cotx.

C. y = tanx.

D. y = -sinx.

Xem đáp án

Chọn A

Câu 4:

Xét hàm số y = cosx trên đoạn $(- \frac{π}{2}; \frac{π}{2})$ . Khẳng định nào sau đây đúng?

A. Trên các khoảng $(- \frac{π}{2}; 0); (0; \frac{π}{2})$ thì hàm số luôn nghịch biến.

B. Hàm số đồng biến trên

(- \frac{π}{2}; 0)

.

C. Hàm số nghịch biến trên

(- \frac{π}{2}; 0)

và đồng biến trên

(0; \frac{π}{2})

.

D. Trên các khoảng

(- \frac{π}{2}; 0); (0; \frac{π}{2})

thì hàm số luôn đồng biến.

Xem đáp án

Chọn B

Câu 5:

Nghiệm của phương trình $s inx = \frac{1}{2}$ là

A. $x = \frac{π}{6} + k π; x = \frac{5 π}{6} + k π$ .

B.

x = \pm \frac{π}{6} + k 2 π

.

C.

x = - \frac{π}{6} + k 2 π; x = - \frac{5 π}{6} + k 2 π

.

D.

x = \frac{π}{6} + k 2 π; x = \frac{5 π}{6} + k 2 π

.

Xem đáp án

Chọn D

$s inx = \frac{1}{2} \Leftrightarrow [\begin{array}{l} x = \frac{π}{6} + k 2 π \\ x = \frac{5 π}{6} + k 2 π \end{array}$

Câu 6:

Phương trình

\tan (3 x - 30 °) = - \frac{\sqrt{3}}{3}

có tập nghiệm là

A. $\{k 180 °, k \in ℤ\}$ .

B.

\{k 60 °, k \in ℤ\}

.

C.

\{k 360 °, k \in ℤ\}

.

D.

\{k 90 °, k \in ℤ\}

.

Xem đáp án

Chọn B

Câu 7:

Tìm tập nghiệm S của phương trình

\cos 2 x = - \frac{\sqrt{2}}{2}

.

A. $S = \{- \frac{3 π}{8} + k 2 π; \frac{3 π}{8} + k 2 π, k \in ℤ\} .$

B.

S = \{- \frac{3 π}{8} + k π; \frac{3 π}{8} + k π, k \in ℤ\} .

C.

S = \{\frac{3 π}{8} + k π; \frac{π}{8} + k π, k \in ℤ\} .

D.

S = \{\frac{3 π}{8} + k 2 π; \frac{π}{8} + k 2 π, k \in ℤ\} .

Xem đáp án

Chọn B

Ta có $\cos 2 x = - \frac{\sqrt{2}}{2} \Leftrightarrow [\begin{array}{l} 2 x = \frac{3 π}{4} + k 2 π \\ 2 x = - \frac{3 π}{4} + k 2 π \end{array} \Leftrightarrow [\begin{array}{l} x = \frac{3 π}{8} + k π \\ x = - \frac{3 π}{8} + k π \end{array} (k \in ℤ) .$

Vậy tập nghiệm của phương trình trên là $S = \{- \frac{3 π}{8} + k π; \frac{3 π}{8} + k π, k \in ℤ\} .$

Câu 8:

Số nghiệm của phương trình

\tan (2 x - \frac{5 π}{6}) + \sqrt{3} = 0

trên khoảng

(0; 3 π)

.

A. 3

B. 8

C. 4

D. 6

Xem đáp án

Chọn D

Câu 9:

Tập nghiệm của phương trình $\sin^{2} x - 5 \sin x + 4 = 0$ là

A. $S = \{\frac{π}{2} + k 2 π, k \in ℤ\}$ .

B.

S = \{k 2 π, k \in ℤ\}

.

C.

S = \{\frac{π}{2} + k 2 π; \arcsin 4 + k 2 π, k \in ℤ\}

.

D.

S = \{\frac{π}{2} + k π, k \in ℤ\}

.

Xem đáp án

Chọn A

Câu 10:

Một hộp có chứa 8 bóng đèn màu đỏ khác nhau và 5 bóng đèn màu xanh khác nhau. Số cách chọn một bóng đèn trong hộp là.

A. 13

B. 5

C. 8

D. 40

Xem đáp án

Chọn A

Có 8 cách chọn một bóng đèn màu đỏ và 5 cách chọn một bóng đèn màu xanh. Nên có tổng số 13 cách chọn một bóng đèn trong hộp.

Câu 11:

Một tổ có 6 học sinh nam và 5 học sinh nữ. Có bao nhiêu cách chọn một học sinh nam và một học sinh nữ để đi tập văn nghệ?

A. $C_{11}^{2}$

B. 30

C. 11

D. $A_{11}^{2}$

Xem đáp án

Chọn B

Chọn một học sinh nam có 6 cách chọn, chọn một học sinh nữ có 5 cách chọn. Theo quy tắc nhân ta có số cách chọn là: 6.5 = 30.

Câu 12:

Từ các số 0,1,2,7,8,9 tạo được bao nhiêu số lẻ có 5 chữ số khác nhau?

A. 288

B. 360

C. 600

D. 312

Xem đáp án

Chọn A

Câu 13:

Một người có 5 cái áo khác nhau trong đó 3 áo màu trắng và 2 áo màu xanh, có 3 cái cà vạt khác nhau trong đó có 1 cà vạt màu đỏ và 2 cà vạt màu vàng. Hỏi người đó có bao nhiêu cách phối một bộ đồ biết nếu chọn áo xanh thì không cà vạt màu đỏ.

A. 5

B. 10

C. 13

D. 15

Xem đáp án

Chọn D

Câu 14:

Số đường chéo của một lục giác lồi là.

A. 6

B. 18

C. 9

D. 30

Xem đáp án

Chọn C

Câu 15:

Có bao nhiêu cách chọn ra 3 bạn từ một lớp có 20 bạn trong đó một bạn làm lớp trưởng, một bạn làm lớp phó, một bạn làm thủ quỹ?

A. $A_{20}^{3}$ .

B.

C_{20}^{3}

.

C.

20^{3}

.

D.

3^{20}

.

Xem đáp án

Chọn A

Mỗi cách chọn ra ba bạn từ một lớp có 20 bạn trong đó một bạn làm lớp trưởng, một bạn làm lớp phó, một bạn làm thủ quỹ là một chỉnh hợp chập 3 của 20.

Nên số cách chọn ra là là $A_{20}^{3}$ .

Câu 16:

Số cách xếp 5 học sinh nam và 5 học sinh nữ thành một hàng dọc là

A. $5! .5!$

B. $10!$

C. 10

D. 25

Xem đáp án

Chọn B

Mỗi cách xếp hàng là một hoán vị của 10 phần tử

Vậy có $10!$ cách xếp hàng.

Câu 17:

Phép tịnh tiến theo

\vec{v}

biến điểm A(1;3) thành điểm A'(1,7). Tìm tọa độ của vectơ tịnh tiến

\vec{v}

.

A. $\vec{v} = (0; - 4)$ .

B.

\vec{v} = (4; 0)

.

C.

\vec{v} = (0; 4)

.

D.

\vec{v} = (0; 5)

.

Xem đáp án

Chọn C

Câu 18:

Cho hình bình hành ABCD. Ảnh của điểm A A qua phép tịnh tiến theo véctơ $\vec{D C}$ là

A. C

B. A

C. D

D. B

Xem đáp án

Chọn D

Câu 19:

Trong mặt phẳng tọa độ Oxy, viết phương trình đường tròn (C') là ảnh của

x^{2} + y^{2} - 2 x + 4 y - 4 = 0

qua phép quay Q(O;

\frac{- π}{2}

).

A. Trong mặt phẳng tọa độ Oxy , viết phương trình đường tròn (C') là ảnh của x^2 + y^2 - 2x + 4y - 4 = 0 qua phép quay . (ảnh 1)

B.

Trong mặt phẳng tọa độ Oxy , viết phương trình đường tròn (C') là ảnh của x^2 + y^2 - 2x + 4y - 4 = 0 qua phép quay . (ảnh 2)

C.

Trong mặt phẳng tọa độ Oxy , viết phương trình đường tròn (C') là ảnh của x^2 + y^2 - 2x + 4y - 4 = 0 qua phép quay . (ảnh 3)

D.

Trong mặt phẳng tọa độ Oxy , viết phương trình đường tròn (C') là ảnh của x^2 + y^2 - 2x + 4y - 4 = 0 qua phép quay . (ảnh 4)

Xem đáp án

Đáp án A

Câu 20:

Mệnh đề nào sau đây là sai?

A. Phép quay $Q_{(O; φ)}$ biến O thành chính nó

B. Phép quay tâm O góc quay

- 180 °

là phép đối xứng tâm O.

C. Nếu

Q_{(O,90 °)} (M) = M^{'} (M \neq O)

thì

O M^{'} > O M

.

D. Phép đối xứng tâm Olà phép quay tâm Ogóc quay

180 °

Xem đáp án

Chọn C

Vì phép quay bảo toàn khoảng cách nên OM' = OM.

Câu 21:

Nếu phép vị tự tỉ số k biến hai điểm M, N lần lượt thành hai điểm M' và N' thì

A. $\vec{M^{'} N^{'}} = k \vec{M N} .$ và $M^{'} N^{'} = - k M N .$

B.

\vec{M^{'} N^{'}} = k \vec{M N} .

và

M^{'} N^{'} = |k| M N .

C.

\vec{M^{'} N^{'}} = |k| \vec{M N}

và

M^{'} N^{'} = k M N .

D.

\vec{M^{'} N^{'}} / / \vec{M N} .

và

M^{'} N^{'} = \frac{1}{2} M N .

Xem đáp án

Chọn D

Theo định lý 1 về tính chất của phép vị tự.

THÔNG HIỂU

Câu 22:

Tập xác định của hàm số

y = \frac{2022}{\tan (x + 2021 π)}

là

A. $D = ℝ \ \{k \frac{π}{2}, k \in ℤ\}$ .

B.

D = ℝ \ \{k π, k \in ℤ\}

.

C.

D = ℝ \ \{\frac{π}{2} + k π, k \in ℤ\}

.

D.

D = ℝ \ \{k 2 π, k \in ℤ\}

.

Xem đáp án

Chọn A

Ta có $\tan (x + 2021 π) = \tan x$

Hàm số xác định khi và chỉ khi $\{\begin{cases} \sin x \neq 0 \\ \cos x \neq 0 \end{cases} \Leftrightarrow \{\begin{cases} x \neq k π \\ x \neq \frac{π}{2} + k π \end{cases} \Leftrightarrow x \neq k \frac{π}{2}, k \in ℤ$ .

Câu 23:

Tìm m để phương trình cosx - 2m + 1 =0 có nghiệm.

A. $m > - \frac{1}{2}$ .

B.

0 < m < 1

.

C.

0 \leq m \leq 1

.

D.

m \geq - \frac{1}{2}

.

Xem đáp án

Chọn C

Câu 24:

Tìm m để phương trình

\sqrt{2} \sin (x + \frac{π}{4}) = m

có nghiệm

x \in (0; \frac{π}{2})

.

A.

[\begin{array}{l} m > 1 \\ m \leq \sqrt{2} \end{array}

.

B.

1 \leq m \leq \sqrt{2}

.

C.

1 \leq m < \sqrt{2}

.

D.

1 < m \leq \sqrt{2}

.

Xem đáp án

Chọn D

Câu 25:

Tổng các nghiệm trên

[- π; π]

của phương trình sin2x = cosx bằng

A.

\frac{3 π}{2} .

B.

2 π .

C.

π .

D.

\frac{3 π}{4} .

Xem đáp án

Chọn C

Câu 26:

Tìm tất cả các nghiệm của phương trình

\tan x + \sqrt{3} \cot x - \sqrt{3} - 1 = 0

là

A. $[\begin{array}{l} x = \frac{π}{4} + k π \\ x = \frac{π}{3} + k π \end{array}, k \in ℤ$ .

B.

[\begin{array}{l} x = - \frac{π}{4} + k π \\ x = \frac{π}{6} + k π \end{array}

.

C.

[\begin{array}{l} x = \frac{π}{4} + k 2 π \\ x = \frac{π}{6} + k 2 π \end{array}

.

D.

[\begin{array}{l} x = \frac{π}{4} + k π \\ x = \frac{π}{6} + k π \end{array}

.

Xem đáp án

Chọn A

Câu 27:

Cho hai đường thẳng $d_{1}$ và $d_{2}$ song song với nhau. Trên $d_{1}$ lấy 5 điểm phân biệt, trên $d_{2}$ lấy 7 điểm phân biệt. Hỏi có bao nhiêu tam giác mà các đỉnh của nó được lấy từ các điểm trên hai đường thẳng $d_{1}$ và $d_{2}$ .

A. 220

B. 7350

C. 1320

D. 175

Xem đáp án

Chọn D

Câu 28:

Cho một lớp học X có 20 học sinh nam và 10 học sinh nữ. Hỏi có tất cả bao nhiêu cách chọn ra 3 học sinh từ lớp học X mà trong đó có ít nhất 2 học sinh nữ?

A. 2920

B. 900

C. 1020

D. 4060

Xem đáp án

Chọn C

Ta thấy bài toán có hai trường hợp thỏa mãn:

Trường hợp 1: Trong số 3 học sinh được chọn có 2 nữ - 1 nam. Số cách chọn là: $C_{10}^{2} . C_{20}^{1}$ .

Trường hợp 2: Trong số 3 học sinh được chọn có 3 nữ - 0 nam. Số cách chọn là: $C_{10}^{3} . C_{20}^{0}$ .

Vậy tổng số cách chọn là: $C_{10}^{2} . C_{20}^{1} + C_{10}^{3} . C_{20}^{0} = 1020$ (cách chọn).

Câu 29:

Sắp xếp 6 nam sinh và 4 nữ sinh vào một dãy ghế hàng ngang có 10 chỗ ngồi. Hỏi có bao nhiêu cách sao cho các nữ sinh luôn ngồi cạnh nhau vào các nam sinh luôn ngồi cạnh nhau?

A. 207360

B. 34560

C. 120096

D. 120960

Xem đáp án

Chọn B

Câu 30:

Cho một lớp học X có 20 học sinh nam và 10 học sinh nữ. Hỏi có tất cả bao nhiêu cách chọn ra 3 học sinh từ lớp học X mà trong đó có ít nhất 2 học sinh nữ?

A. 2920

B. 900

C. 1020

D. 4060

Xem đáp án

Chọn C

Ta thấy bài toán có hai trường hợp thỏa mãn:

Trường hợp 1: Trong số 3 học sinh được chọn có 2 nữ - 1 nam. Số cách chọn là: $C_{10}^{2} . C_{20}^{1}$ .

Trường hợp 2: Trong số 3 học sinh được chọn có 3 nữ - 0 nam. Số cách chọn là: $C_{10}^{3} . C_{20}^{0}$ .

Vậy tổng số cách chọn là: $C_{10}^{2} . C_{20}^{1} + C_{10}^{3} . C_{20}^{0} = 1020$ (cách chọn).

Câu 31:

Trong mặt phẳng toạ độ Oxy, cho véc tơ $\vec{v} = (3; 3), A (2; 2), B (0; - 6)$ . Ảnh của đường tròn đường kính AB qua $T_{\vec{v}}$ là

A. ${(x - 4)}^{2} + {(y - 1)}^{2} = 17$ .

B.

{(x - 4)}^{2} + {(y - 1)}^{2} = 68

.

C.

{(x + 4)}^{2} + {(y + 1)}^{2} = 17

.

D.

x^{2} + y^{2} + 8 x + 2 y - 4 = 0

.

Xem đáp án

Chọn A

Câu 32:

Trong mặt phẳng tọa độ Oxy, cho $∆ A B C$ biết A(2,4), B(5,1), C(-1,-2). Phép tịnh tiến theo véctơ BC biến $∆ A B C$ thành $∆ A' B' C'$ tương ứng các điểm. Tọa độ trọng tâm G' của $∆ A' B' C'$ là:

A. G'(-4,-2)

B. G'(4,2)

C. G'(4,-2)

D. G'(-4,4)

Xem đáp án

Đáp án A.

Câu 33:

Trong mặt phẳng tọa độ Oxy cho hai đường tròn $(C_{1})$ và $(C_{2})$ bằng nhau có phương trình lần lượt là ${(x - 1)}^{2} + {(y + 2)}^{2} = 16$ và ${(x + 3)}^{2} + {(y - 4)}^{2} = 16$ . Giả sử T là phép tịnh tiến theo vectơ $\vec{u}$ biến $(C_{1})$ thành $(C_{2})$ . Tìm tọa độ của vectơ $\vec{u}$ .

A.

\vec{u} = (- 4; 6) .

B.

\vec{u} = (4; - 6) .

C.

\vec{u} = (3; - 5) .

D.

\vec{u} = (8; - 10) .

Xem đáp án

Chọn A

Câu 34:

Cho tam giác đều tâm O. Hỏi có bao nhiêu phép quay tâm O góc quay $α$ , $0 < α \leq 2 π$ biến tam giác trên thành chính nó?

A. Một.

B. Hai.

C. Ba.

D. Bốn.

Xem đáp án

Chọn C

Câu 35:

Cho hai đường thẳng cắt nhau d và d'. Có bao nhiêu phép vị tự biến mỗi đường thẳng thành chính nó.

A. 0

B. 1

C. 2

D. Vô số

Xem đáp án

Chọn D

Tâm vị tự là giao điểm của d và d'. Tỉ số vị tự là số k khác 0

(hoặc tâm vị tự tùy ý, tỉ số k = 1 - đây là phép đồng nhất)

Câu 36:

Giải phương trình: $\cos^{2} (\frac{π}{3} + x) + 4 \cos (\frac{π}{6} - x) = 4$

Xem đáp án

Giải phương trình: cos^2 (pi/3 + x) + 4cos( pi/6 - x) = 4 (ảnh 1)

Câu 37:

Trong mặt phẳng tọa độ Oxy, cho đường thẳng d: x + 2y = 0. Phép đồng dạng là phép thực hiện liên tiếp qua phép vị tự tâm I(1;-2) tỉ số k = 3 và phép quay tâm O góc quay $\frac{π}{2}$ sẽ biến đường thẳng d thành đường thẳng nào sau đây?

Xem đáp án

Trong mặt phẳng tọa độ Oxy , cho đường thẳng d: x + 2y =0 . Phép đồng dạng là phép thực hiện liên tiếp qua phép (ảnh 1)

Câu 38:

Có bao nhiêu số tự nhiên có 7 chữ số có nghĩa, biết rằng chữ số 2 có mặt đúng 2 lần, chữ số 3 có mặt đúng 3 lần, các chữ số còn lại có mặt không quá một lần?

Xem đáp án

Có bao nhiêu số tự nhiên có 7 chữ số có nghĩa, biết rằng chữ số 2 có mặt đúng 2 lần, chữ số 3 có mặt đúng 3 lần, các chữ số còn lại có mặt không quá một lần? (ảnh 1)

Câu 39:

Thầy A có 30 câu hỏi khác nhau gồm 5 câu khó, 15 câu trung bình và 30 câu dễ. Từ 5 câu hỏi đó có thể lập được bao nhiêu đề kiểm tra, mỗi đề gồm 5 câu hỏi khác nhau, sao cho trong mỗi đề nhất thiết phải có đủ cả 3 câu và số câu dễ không ít hơn 2?

Xem đáp án