Đề kiểm tra cuối học kì 2 Toán 7 Cánh Diều - Đề 01 có đáp án
-
1751 lượt thi
-
22 câu hỏi
-
90 phút
Danh sách câu hỏi
Câu 1:
Cho các dãy dữ liệu:
(1) Tên của mỗi bạn học sinh trong lớp 7A.
(2) Số lượng học sinh của các lớp 7 đạt điểm 10 thi giữa học kì I.
(3) Số nhà của mỗi bạn học sinh lớp 7B.
(4) Số lượng nhóm nhạc yêu thích của mỗi bạn học sinh trong lớp.
Trong các dãy dữ liệu trên, dãy dữ không phải là số là
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
Tên của mỗi bạn học sinh trong lớp 7A là dãy dữ liệu không phải là số.
Câu 2:
Biểu đồ dưới đây cho biết tỉ lệ các loại kem bán được trong một ngày của một cửa hàng kem.
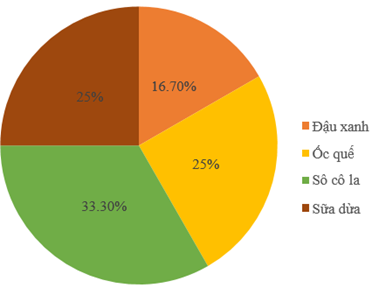
Biết rằng một ngày cửa hàng đó bán được 100 cái kem. Số lượng kem ốc quế bán được trong một ngày là bao nhiêu?
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
Số lượng kem ốc quế bán được trong một ngày là: \(\frac{{100.25}}{{100}} = 25\) cái.
Câu 3:
Tung hai con xúc xắc màu xanh và đỏ rồi quan sát số chấm xuất hiện trên mặt hai con xúc xắc. Xét biến cố A: “Số chấm trên mặt hai con xúc xắc bằng nhau”. Khẳng định nào sau đây là đúng?
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Khi tung hai con xúc xắc màu xanh và đỏ thì số chấm xuất hiện trên mặt hai con xúc xắc có thể bằng nhau, chẳng hạn hai con xúc xắc đều xuất hiện 1 chấm; số chấm xuất hiến trên mặt hai con xúc xắc có thể không bằng nhau, chẳng hạn con xúc xắc xanh xuất hiện mặt 1 chấm, con xúc xắc đỏ xuất hiện mặt 2 chấm.
Vậy biến cố A: “Số chấm trên mặt hai con xúc xắc bằng nhau” là biến cố ngẫu nhiên.
Câu 4:
Một chiếc bình thủy tinh đựng 1 ngôi sao giấy màu tím, 1 ngôi sao giấy màu xanh, 1 ngôi sao giấy màu vàng, 1 ngôi sao giấy màu đỏ. Các ngôi sao có kích thước và khối lượng như nhau. Lấy ngẫu nhiên 1 ngôi sao từ trong bình. Cho biến cố Y: “Lấy được 1 ngôi sao màu tím hoặc màu đỏ”. Xác suất của biến cố Y là
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
Trong bình có tất cả 4 ngôi sao có màu khác nhau: màu tím, màu xanh, màu vàng và màu đỏ.
Do các ngôi sao có cùng kích thước và khối lượng như nhau nên các ngôi sao đều có cùng khả năng được chọn.
Vì trong bình có 1 ngôi sao màu tím và 1 ngôi sao màu đỏ nên có 2 kết quả làm cho biến cố Y: “Lấy được 1 ngôi sao màu tím hoặc màu đỏ” xảy ra.
Do đó xác suất của biến cố Y là \[P\left( Y \right) = \frac{2}{4} = \frac{1}{2}.\]
Câu 5:
Một người đi bộ trong x (giờ) với vận tốc 4 (km/h) và sau đó đi bằng xe đạp trong y (giờ) với vận tốc 18 (km/h). Biểu thức đại số biểu thị tổng quãng đường đi được của người đó là
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
Quãng đường mà người đó đi bộ là : 4.x = 4x (km)
Quãng đường mà người đó đi bằng xe đạp là: 18.y = 18y (km)
Tổng quãng đường đi được của người đó là: 4x + 18y (km).
Câu 6:
Giá trị của biểu thức A = –(2a + b) tại a = 1; b = 3 là
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
Thay a = 1, b = 3 vào biểu thức A ta được:
A = –(2.1 + 3) = –(2 + 3) = –5.
Câu 7:
Hệ số tự do của đa thức 10 – 9x2 – 7x5 + x6 – x4 là
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
Sắp xếp đa thức đã cho theo lũy thừa giảm dần của biến y như sau:
10 – 9x2 – 7x5 + x6 – x4
= x6 – 7x5 – x4 – 9x2 + 10
Hệ số tự do của đa thức đã cho là 10.
Câu 8:
Cho đa thức A(t) = 2t2 – 3t + 1. Phần tử nào trong tập hợp {‒1; 0; 1; 2} là nghiệm của A(t)?
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Xét đa thức A(t) = 2t2 – 3t + 1, ta có:
A(‒1) = 2.(‒1)2 – 3.(‒1) + 1 = 2 + 3 + 1 = 6 ≠ 0.
A(0) = 2.02 – 3.0 + 1 = 0 + 0 + 1 = 1 ≠ 0.
A(1) = 2.12 – 3.1 + 1 = 2 ‒ 3 + 1 = 0.
A(2) = 2.22 – 3.2 + 1 = 8 ‒ 6 + 1 = 3 ≠ 0.
Vậy số 1 là là một nghiệm của A(t).
Câu 9:
Trong một tam giác, đối diện với cạnh nhỏ nhất là một
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
Trong một tam giác, đối diện với cạnh nhỏ nhất là góc nhỏ nhất, mà góc nhỏ nhất của một tam giác là góc nhọn.
Câu 10:
Cho tam giác ABC có \[\widehat A = 35^\circ \], \(\widehat B = 45^\circ \). Số đo góc C là:
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
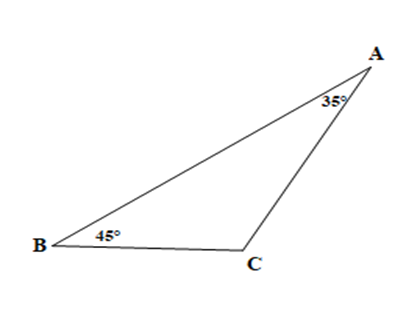
Xét DABC có: \(\widehat A + \widehat B + \widehat C = 180^\circ \) ( định lí tổng ba góc trong một tam giác)
Suy ra \(\widehat C = 180^\circ - \widehat A - \widehat B = 180^\circ - 35^\circ - 45^\circ = 100^\circ \).
Câu 11:
Bộ ba số đo nào dưới đây có thể là độ dài ba cạnh của một tam giác?
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
Trong một tam giác, tổng độ dài hai cạnh bất kì lớn hơn độ dài cạnh còn lại.
Ta thấy:
3 + 4 = 7 nên bộ ba số đo 7 cm, 3 cm, 4 cm không thể là ba cạnh của một tam giác.
3 + 5 > 7 nên bộ ba số đo 7 cm, 3 cm, 5 cm có thể là ba cạnh của một tam giác.
2 + 3 < 7 nên bộ ba số đo 7 cm, 3 cm, 2 cm không thể là ba cạnh của một tam giác.
3 + 3 < 7 nên bộ ba số đo 7 cm, 3 cm, 4 cm không thể là ba cạnh của một tam giác.
Câu 12:
Trong một tam giác, trực tâm là giao điểm của ba đường nào?
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
Trong một tam giác, trực tâm là giao điểm của ba đường cao.
Câu 13:
Biểu đồ dưới đây biểu diễn lượng mưa (đơn vị: mm) của hai tỉnh Lai Châu và Cà Mau trong các năm 2016 – 2020.

 Xem đáp án
Xem đáp án
Tổng lượng mưa tại mỗi tỉnh Lai Châu trong giai đoạn 2016 – 2020 là:
2 186 + 3 179 + 2 895 + 2 543 + 2 702 = 13 505 (mm).
Tổng lượng mưa tại mỗi tỉnh Cà Mau trong giai đoạn 2016 – 2020 là:
2 304 + 2 175 + 2 008 + 2 263 + 2 395 = 11 145 (mm).
Câu 14:
Biểu đồ dưới đây biểu diễn lượng mưa (đơn vị: mm) của hai tỉnh Lai Châu và Cà Mau trong các năm 2016 – 2020.
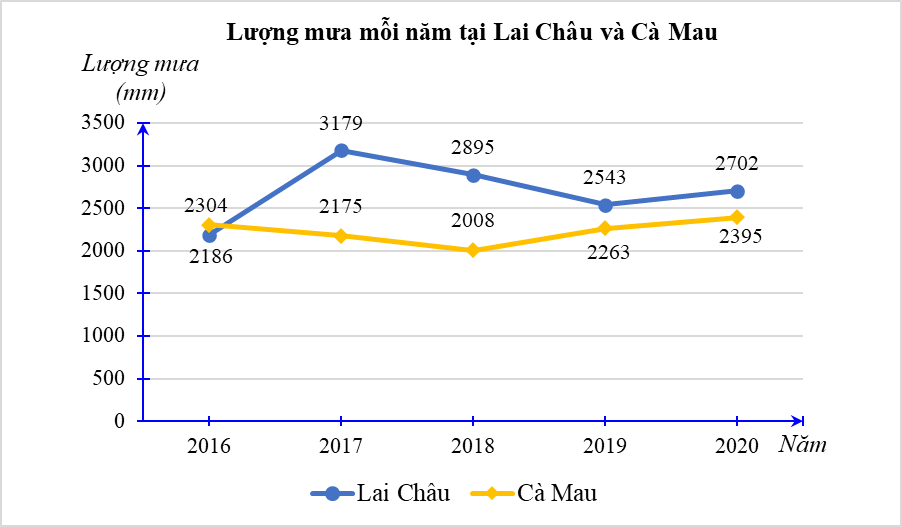
Năm 2017, lượng mưa tại Cà Mau bằng bao nhiêu phần trăm lượng mưa tại Lai Châu (làm tròn kết quả với độ chính xác 0,005)?
 Xem đáp án
Xem đáp án
Năm 2017, lượng mưa tại Cà Mau và Lai Châu lần lượt là 2 175 mm và 3 179 mm.
Trong năm 2017, lượng mưa tại Cà Mau bằng số phần trăm lượng mưa tại Lai Châu là: \(\frac{{2\,\,175}}{{3\,\,179}}.100\% \approx 68,42\% \).
Câu 15:
Biểu đồ dưới đây biểu diễn lượng mưa (đơn vị: mm) của hai tỉnh Lai Châu và Cà Mau trong các năm 2016 – 2020.
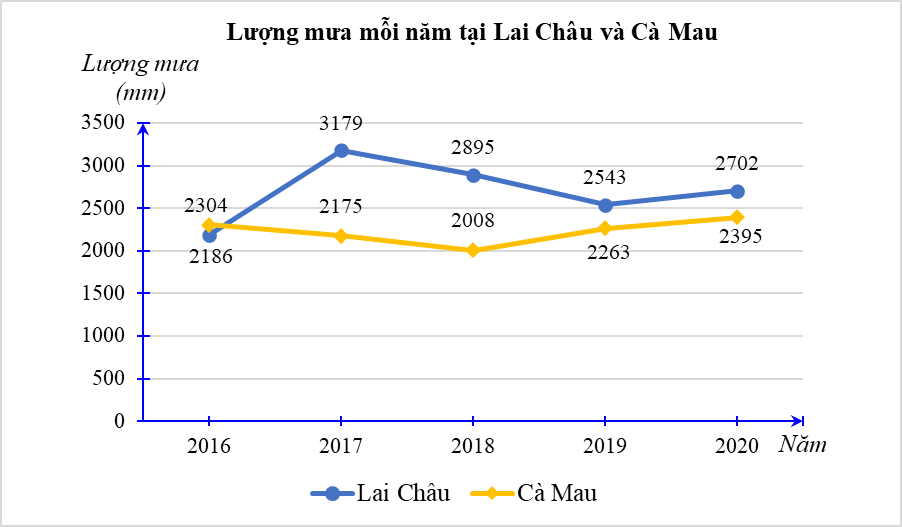
Chọn ngẫu nhiên 1 năm trong 5 năm đó. Tính xác suất của các biến cố sau:
A: “Tại năm được chọn, lượng mưa ở Cà Mau cao hơn ở Lai Châu”;
B: “Tại năm được chọn, lượng mưa ở Cà Mau thấp hơn 25 m”;
 Xem đáp án
Xem đáp án
• Quan sát biểu đồ trên thấy có 1 năm mà lượng mưa ở Cà Mau cao hơn lượng mưa ở Lai Châu là: năm 2016.
Vì chọn ngẫu nhiên một năm nên xác suất của biến cố A: “Tại năm được chọn lượng mưa ở Cà Mau cao hơn ở Lai Châu” là P(A) = \(\frac{1}{5}.\)
• Ta có: 25 m = 25 000 mm.
Quan sát biểu đồ ta thấy tất cả các năm 2016, 2017, 2018, 2019, 2020 đều có lượng mưa ở Cà Mau thấp hơn 25 000 mm.
Do đó biến cố B: “Tại năm được chọn, lượng mưa ở Cà Mau thấp hơn 25 m” là biến cố chắc chắn nên P(B) = 1.
Vậy P(A) = \(\frac{1}{5}\), P(B) = 1.
Câu 16:
Cho biết A(x) – (9x3 + 8x2 – 2x – 7) = –9x3 – 8x2 + 5x + 11.
Tìm đa thức A(x) Xem đáp án
Xem đáp án
Ta có A(x) = –9x3 – 8x2 + 5x + 11 + (9x3 + 8x2 – 2x – 7)
A(x) = –9x3 – 8x2 + 5x + 11 + 9x3 + 8x2 – 2x – 7
A(x) = 3x + 4
Câu 17:
A(x) – (9x3 + 8x2 – 2x – 7) = –9x3 – 8x2 + 5x + 11.
Xác định bậc và hệ số cao nhất của đa thức A(x).
 Xem đáp án
Xem đáp án
Đa thức A(x) có bậc là 1 và hệ số cao nhất là 3.
Câu 18:
Cho biết A(x) – (9x3 + 8x2 – 2x – 7) = –9x3 – 8x2 + 5x + 11.
Tìm đa thức M(x) sao cho M(x) = A(x).B(x) biết B(x) = –x2 + x.
 Xem đáp án
Xem đáp án
M(x) = A(x).B(x)
M(x) = (3x + 4).(–x2 + x)
= 3x.(–x2 + x) + 4(–x2 + x)
= –3x3 + 3x2 – 4x2 + 4x
= –3x3 – x2 + 4x.
Câu 19:
Cho biết A(x) – (9x3 + 8x2 – 2x – 7) = –9x3 – 8x2 + 5x + 11.
Tính M(‒1), từ đó kết luận số ‒1 có phải là nghiệm của đa thức M(x) hay không.
 Xem đáp án
Xem đáp án
M(‒1) = –3.(‒1)3 – (‒1)2 + 4.(‒1) = 3 – 1 – 4 = ‒2 ≠ 0.
Vậy số ‒1 không là nghiệm của đa thức M(x).
Câu 20:
Cho tam giác ABC vuông tại A. Trên cạnh BC lấy điểm E sao cho BE = BA, trên tia BA lấy điểm F sao cho BF = BC. Kẻ tia BD là tia phân giác của góc ABC (D thuộc AC). Chứng minh rằng:
DABD = DEBD từ đó suy ra AD = ED.
 Xem đáp án
Xem đáp án
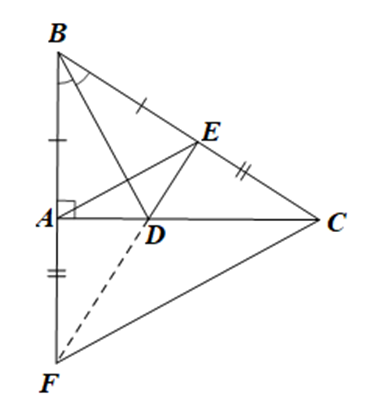
Xét DABD và DEBD có:
BA = BE (giả thiết);
\(\widehat {ABD} = \widehat {BBD}\) (do BD là tia phân giác của góc ABC);
BD là cạnh chung.
Do đó DABD = DEBD (c.g.c)
Suy ra AD = ED (hai cạnh tương ứng).
Câu 21:
Cho tam giác ABC vuông tại A. Trên cạnh BC lấy điểm E sao cho BE = BA, trên tia BA lấy điểm F sao cho BF = BC. Kẻ tia BD là tia phân giác của góc ABC (D thuộc AC). Chứng minh rằng:
BD là đường trung trực của đoạn thẳng AE và AD < DC.
 Xem đáp án
Xem đáp án

• Do BA = BE nên B nằm trên đường trung trực của AE.
Do AD = ED nên D nằm trên đường trung trực của AE.
Suy ra BD là đường trung trực của AE.
• Do DABD = DEBD nên \(\widehat {BED} = \widehat {BAD} = 90^\circ \) (hai góc tương ứng)
Xét DDCE vuông tại E có DC là cạnh huyền nên DC là cạnh lớn nhất.
Do đó DC > DE.
Mà AD = DE nên AD < DC.
Câu 22:
Cho tam giác ABC vuông tại A. Trên cạnh BC lấy điểm E sao cho BE = BA, trên tia BA lấy điểm F sao cho BF = BC. Kẻ tia BD là tia phân giác của góc ABC (D thuộc AC). Chứng minh rằng:
Ba điểm E, D, F thẳng hàng.
 Xem đáp án
Xem đáp án
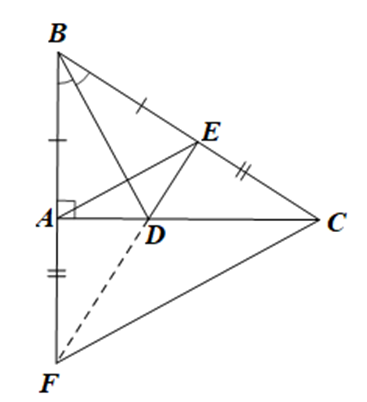
• Tam giác BAE có BA = BE nên cân tại B.
Do đó \(\widehat {BAE} = \widehat {BEA}\).
Mà \(\widehat {ABE} + \widehat {BAE} + \widehat {BEA} = 180^\circ \).
Suy ra \(\widehat {BAE} = \widehat {BEA} = \frac{{180^\circ - \widehat {ABE}}}{2}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left( 1 \right)\)
Tương tự với tam giác BFC ta cũng có \(\widehat {BFC} = \widehat {BCF} = \frac{{180^\circ - \widehat {FBC}}}{2}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left( 2 \right)\)
Từ (1) và (2) suy ra \(\widehat {BAE} = \widehat {BFC}\).
Mà hai góc này ở vị trí đồng vị nên AE // FC.
Lại có AE ⊥ BD (do BD là đường trung trực của AE)
Do đó BD ⊥ FC.
• Xét DBFC có BD ⊥ FC, CA ⊥ BF, BD cắt CA tại D nên D là trực tâm của DBFC.
Suy ra FD ⊥ BC.
Mà DE ⊥ BC (do \(\widehat {BED} = 90^\circ \))
Do đó ba điểm F, D, E thẳng hàng.
