Đề thi giữa kì 1 Toán 7 KNTT có đáp án - Đề 2
-
2899 lượt thi
-
23 câu hỏi
-
90 phút
Danh sách câu hỏi
Câu 1:
Khẳng định nào sau đây đúng nhất:
Nếu a ∈ ℤ thì
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Với mọi a ∈ ℤ ta đều có thể viết được dưới dạng nên a ∈ ℚ.
Mọi số nguyên, số hữu tỉ đều là số thực nên a ∈ ℝ.
Vậy ta chọn phương án C.
Câu 2:
Trong các số sau, số nào không phải là số đối của số ?
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Ta có nên ‒1,5 không phải là số đối của số .
Vậy ta chọn phương án C.
Câu 3:
Cho các số hữu tỉ sau . Sắp xếp các số trên theo thứ tự giảm dần ta được:
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
Vì ‒1 > ‒3 > ‒9 > ‒12
Nên (so sánh các phân số cùng mẫu)
Nên sắp xếp theo thứ tự giảm dần ta được dãy: .
Câu 4:
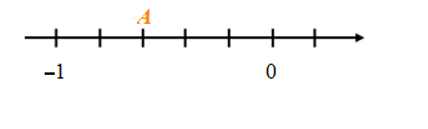
Điểm A trên trục số trong hình vẽ dưới đây biểu diễn số hữu tỉ nào?
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Quan sát trục số ta thấy đoạn thẳng đơn vị từ 0 đến 1 chia thành 5 đoạn bằng nhau, lấy một đoạn làm đơn vị mới, đơn vị mới bằng đơn vị cũ.
Điểm A nằm bên trái 0 và cách 0 một đoạn bằng 3 đơn vị mới nên điểm A biểu diễn số .
Câu 5:
Trong các số sau đây số nào là số thập phân vô hạn không tuần hoàn:
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
Số 2,64575… là số thập phân vô hạn và có phần thập phân không lặp lại theo một chu kì nào.
Do đó số 2,64575… là số thập phân vô hạn không tuần hoàn.
Câu 7:
Cho x = -12. Tính |x + 2|.
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
Với x = -12, ta có:
|x + 2| = |-12 + 2| = | -10| = -(-10) = 10.
Câu 8:
Khẳng định nào sau đây là đúng?
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Ta có: x2 = 3.
Suy ra .
Biểu diễn các số thực x trên trục số là:
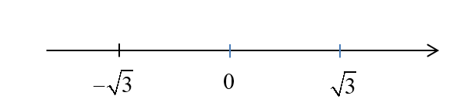
Nhìn vào trục số ta thấy điểm biểu diễn nằm trước điểm 0 trên trục số; điểm biểu diễn nằm sau điểm 0 trên trục số.
Hai số và cách số 0 một khoảng bằng nhau và bằng trên trục số.
Vậy chọn phương án C.
Câu 10:
Cho , tia Ot là tia phân giác của góc xOy. Số đo góc xOt là:
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Ta có Ot là tia phân giác góc xOy
Suy ra .
Câu 11:
Qua điểm A nằm ngoài đường thẳng x, ta vẽ hai đường thẳng qua A và song song với x thì:
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
Theo tiên đề Euclid ta có: Qua một điểm ở ngoài một đường thẳng chỉ có một đường thẳng song song với đường thẳng đó
Do đó, qua điểm A nằm ngoài đường thẳng x, ta vẽ hai đường thẳng qua A và song song với x thì hai đường thẳng đó phải trùng nhau.
Vậy t chọn phương án A.
Câu 12:
a) Biết biểu thức 68 . 125 viết được dưới dạng 2a . 3b. Tính a – b.
 Xem đáp án
Xem đáp án
a) Ta có:
68 . 125 = (2 . 3)8 . (3. 22)5 = 28 . 38 . 35 . (22)5
= 28 . 22 . 5 . 38 + 5 = 28 + 10 . 313 = 218 . 313.
Khi đó a = 18 và b = 13.
Do đó a – b = 18 – 13 = 5.
Vậy a – b = 5.
Câu 13:
b) Cho a = = 9,94987471… và b = 5,(123).
i) Hai số b là số thập phân hữu hạn, số thập phân vô hạn tuần hoàn hay số vô tỉ? Tìm chữ số thập phân thứ năm của số b.
 Xem đáp án
Xem đáp án
i) Số b = 5,(123) = 5,12312312… là số thập phân vô hạn tuần hoàn có chu kì là 123.
Chữ số thập phân thứ năm của số b là chữ số 2.
Câu 14:
ii) Ước lượng tích của a và b.
 Xem đáp án
Xem đáp án
ii) Làm tròn a = = 9,94987471… đến hàng đơn vị ta được a ≈ 10.
Làm tròn b = 5,12312312… đến hàng đơn vị ta được b ≈ 5.
Khi đó ước lượng tích của a và b là a . b ≈ 10 . 5 = 50.
Câu 15:
Tính giá trị của các biểu thức sau (tính hợp lí nếu có thể):
a) ;
 Xem đáp án
Xem đáp án
a)
= 16 + 8 – 1 + 4
= 27
Câu 20:
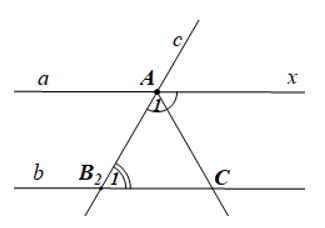
Cho ba đường thẳng a, b, c như hình vẽ sau:
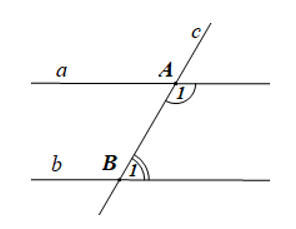
Biết và là hai góc bù nhau.
 Xem đáp án
Xem đáp án
a)
|
GT |
a, b, c là các đường thẳng; c cắt a tại A, c cắt b tại B,
c) AC là tia phân giác của góc A1. |
|
KL |
b) Tính , a // b. c – ii) Tính |
Câu 21:
b) Tính số đo , từ đó chứng minh a // b.
 Xem đáp án
Xem đáp án
b) • Do là hai góc bù nhau nên
Mà (giả thiết) nên ta có
Hay
Do đó
Suy ra
• Ta có (hai góc kề bù).
Suy ra
Do đó (cùng bằng 120°).
Mà hai góc này ở vị trí so le trong.
Suy ra a // b (dấu hiệu nhận biết).
Vậy a // b.
Câu 22:
c) Tia phân giác của góc A1 cắt đường thẳng b tại C. Tính số đo góc ACB.
 Xem đáp án
Xem đáp án
c) Vì AC là tia phân giác của góc A1 nên ta có:
(tính chất tia phân giác).
Mà a // b (chứng minh câu b)
Do đó (hai góc so le trong).
Vậy