Đề thi Học kì 1 Toán 7 Cánh diều có đáp án (Đề 1)
-
1258 lượt thi
-
19 câu hỏi
-
90 phút
Danh sách câu hỏi
Câu 1:
Cho các số sau: Hãy cho biết số nào không phải là số hữu tỉ?
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
Số hữu tỉ là số viết được dưới dạng phân số với a, b ∈ ℤ, b ≠ 0.
Nhận thấy: số viết được dưới dạng phân số có 3; 0 ∈ ℤ nhưng có mẫu bằng 0.
Do đó không phải là số hữu tỉ.
Câu 3:
Chu kỳ của số thập phân vô hạn tuần hoàn −4,31(2) là:
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
Số thập phân vô hạn tuần hoàn −4,31(2) có chu kỳ là 2.
Câu 4:
Tập hợp các số thực được kí hiệu là:
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
Tập hợp các số thực được kí hiệu là ℝ.
Câu 5:
Cho đường thẳng c cắt hai đường thẳng song song a và b. Khi đó, tiên đề Euclid suy ra tính chất nào sau đây?
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
Cho đường thẳng c cắt hai đường thẳng song song a và b. Khi đó tiên đề Euclid suy ra các tính chất:
+ Hai góc so le trong bằng nhau;
+ Hai góc đồng vị bằng nhau;
Vậy ta chọn phương án D.
Câu 6:
Cho các số sau số nào viết được dưới dạng số thập phân hữu hạn?
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
Ta có: .
Các số 0,75; 1,25 là số thập phân hữu hạn.
Các số 0,66...6; 1,333...3 là số thập phân vô hạn tuần hoàn.
Do đó các số là số thập phân hữu hạn.
Câu 7:
Khẳng định nào không đúng về các cạnh bên của hình lăng trụ đứng tứ giác?
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
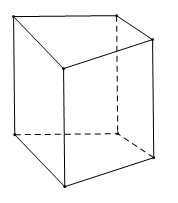
Hình lăng trụ đứng tứ giác có các mặt bên là những hình chữ nhật, các cạnh bên song song và bằng nhau.
Vậy D sai.
Câu 8:
Trong các khẳng định sau, khẳng định nào đúng?
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
+ Hai đường thẳng cắt nhau tạo thành hai cặp góc đối đỉnh.
Ví dụ hai đường thẳng xx’ và yy’ cắt nhau tại A sẽ tạo thành hai cặp góc đối đỉnh là và ; và .
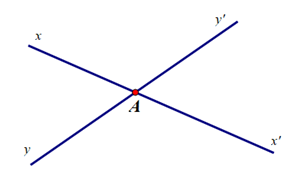
Do đó khẳng định D đúng.
+ Khẳng định A, B, C sai vì:
Hai góc có tổng bằng 180° là hai góc bù nhau.
Hai góc vừa kề nhau, vừa bù nhau là hai góc kề bù.
Hai góc kề nhau là hai góc có một cạnh chung và hai cạnh còn lại nằm khác phía đối với đường thẳng chứa cạnh chung đó.
Câu 9:
Phát biểu định lí sau bằng lời:
|
GT |
a ⊥ c; b⊥ c |
|
KL |
a // b |
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Theo đề bài, ta có:
- Giả thiết: Hai đường thẳng a và b cùng vuông góc với đường thẳng c.
- Kết luận: Đường thẳng a song song với đường thẳng b.
Từ đó ta có định lí: “Nếu hai đường thẳng phân biệt cùng vuông góc với đường thẳng thứ ba thì chúng cắt nhau”.
Câu 10:
Cho hình hộp chữ nhật có kích thước như hình vẽ.
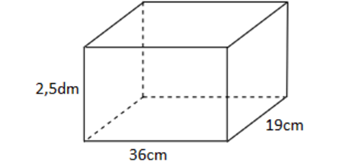
Diện tích xung quanh của hình hộp chữ nhật là:
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
Đổi 2,5 dm = 25 cm.
Diện tích xung quanh của hình hộp chữ nhật là:
Sxq = 2 . (36 + 19) . 25 = 2 750 (cm2)
Vậy chọn đáp án A.
Câu 11:
Một ô tô đi quãng đường 100 km với vận tốc v (km/h) và thời gian t (h). Chọn câu đúng về mối quan hệ vủa v và t.
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
Theo đề bài, ta có: v . t = 100
Suy ra .
Do đó v và t là hai đại lượng tỉ lệ nghịch với hệ số tỉ lệ 100.
Câu 12:
Trong tháng 5 vừa qua, tỉ số sản phẩm làm được của An và Bình trong một phân xưởng là 0,95. Hỏi An và Bình lần lượt làm được bao nhiêu sản phẩm, biết rằng An làm nhiều hơn Bình là 10 sản phẩm?
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Gọi x, y (sản phẩm) lần lượt là số sản phẩm của An và Bình làm được (x, y Î ℕ*).
Tỉ số sản phẩm làm được của An và Bình là 0,95 nên:
hay .
Do đó .
Vì An làm nhiều hơn Bình là 10 sản phẩm nên: y − x = 10.
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
.
Suy ra: x = 19 . 10 = 190; y = 20 . 10 = 200.
Do đó x = 190; y = 200 (thỏa mãn).
Vậy số sản phẩm An và Bình làm được lần lượt là: 190 sản phẩm và 200 sản phẩm.
Câu 13:
Thực hiện phép tính:
a) ;
b) ;
c) ;
d) .
 Xem đáp án
Xem đáp án
.
c)
= 0,1 . 20 + 0,2 . 40
= 2 + 8 = 10.
d)
.
Câu 14:
Người ta đào một đoạn mương dài 20 m, sâu 1,5 m. Bề mặt của mương rộng 1,8 m và đáy mương rộng 1,2 m.
a) Tính thể tích khối đất phải đào.
 Xem đáp án
Xem đáp án
a) Gọi đoạn mương có dạng hình lăng trụ đứng tứ giác BCC’B’.ADD’A’ có đáy là hình thang BCC’B’ (như hình vẽ).
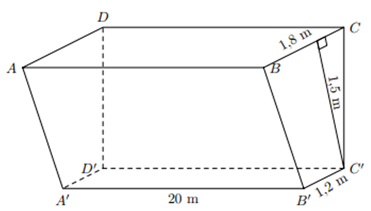
Diện tích đáy hình thang BCC’B’ là:
(m2)
Thể tích khối đất phải đào là:
V = 2,25 . 20 = 45 (m3)
Vậy thể tích khối đất phải đào là 45 m3.
Câu 15:
b) Người ta chuyển khối đất trên để rải lên một mảnh đất hình chữ nhật có kích thước 30 m × 40 m. Tính bề dày của lớp đất rải lên trên mảnh đất đó.
 Xem đáp án
Xem đáp án
b) Khối đất được rải lên bề mặt hình chữ nhật có dạng hình hộp chữ nhật MNPQ.M’N’P’Q’ có chiều dài là M’N’ = 40 m, chiều rộng N’P’ = 30 m và chiều cao PP’ = h (m) (như hình vẽ).
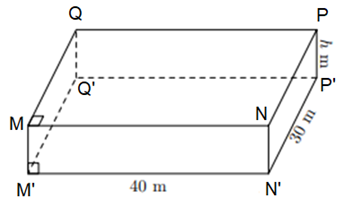
Theo đề bài, người ta chuyển khối đất trên để rải lên một mảnh đất hình chữ nhật.
Do đó, thể tích hình lăng trụ đứng tứ giác BCC’B’.ADD’A’ bằng thể tích hình hộp chữ nhật MNPQ.M’N’P’Q’ và đều bằng 45 m3.
Diện tích mảnh đất hình chữ nhật là:
S = 30 × 40 = 1 200 (m2)
Bề dày của lớp đất rải lên trên mảnh đất đó là:
(m).
Vậy bề dày của lớp đất rải lên trên mảnh đất là 0,0375 m.
Câu 16:
Một nhân viên văn phòng có thể đánh máy được 160 từ trong 2,5 phút. Hỏi cần bao nhiêu phút để người đó đánh được 800 từ? (giả thiết rằng thời gian để đánh được các từ là như nhau).
 Xem đáp án
Xem đáp án
Gọi x (phút) là thời gian cần thiết để người đó đánh được 800 từ (x > 0).
Vì thời gian và số từ đánh được là hai đại lượng tỉ lệ thuận nên ta có:
(thỏa mãn)
Vậy cần 12,5 phút để người đó đánh được 800 từ.
Câu 17:
Cho hình vẽ sau, hãy chỉ ra:
a) Các cặp góc kề bù;
b) Các cặp góc đối đỉnh.
 Xem đáp án
Xem đáp án
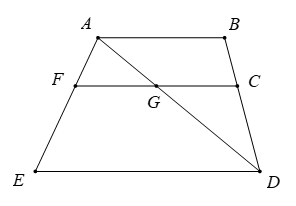
Quan sát hình vẽ, ta thấy:
a) Các cặp góc kề bù là: và ; và ; và ; và .
b) Cạnh AG của là tia đối của cạnh DG của ;
Cạnh FG của là tia đối của cạnh CG của
Do đó và là hai góc đối đỉnh.
Cạnh FG của là tia đối của cạnh CG của ;
Cạnh DG của là tia đối của cạnh AG của
Do đó và là hai góc đối đỉnh.
Vậy các cặp góc đối đỉnh là: và ; và .
Câu 18:
Để nâng cao hiệu quả phòng chống dịch bệnh, học sinh phải thực hiện việc test nhanh Covid trước khi đến trường. Giá ban đầu để test mẫu gộp là 40 000 đồng/1 học sinh, mẫu đơn là 100 000 đồng/1 học sinh. Do lớp 7A test sau ngày 21/2/2022 nên được giảm giá 30%.
a) Tính chi phí test nhanh Covid của lớp 7A biết có 13 em test mẫu gộp, 22 em test mẫu đơn.
 Xem đáp án
Xem đáp án
a) Chi phí test Covid của lớp 7A khi chưa được giảm giá là:
13 . 40 000 + 22 . 100 000 = 2 720 000 (đồng)
Chi phí test Covid của lớp 7A sau khi được giảm giá là:
2 720 000 . 30% = 1 904 000 (đồng)
Câu 19:
b) Nếu chi phí test nhanh Covid cho 35 học sinh lớp 7A là 2 030 000 đồng thì có bao nhiêu em test mẫu đơn, bao nhiêu em test mẫu gộp?
 Xem đáp án
Xem đáp án
b) Giả sử tất cả 35 em được test mẫu đơn thì chi phí là:
35 . 100 000 . 0,7 = 2 450 000 (đồng)
Khi đó chi phí test mẫu gộp nhiều hơn so với thực tế là:
2 450 000 – 2 030 000 = 420 000 (đồng)
Số tiền test 1 mẫu đơn nhiều hơn test 1 mẫu gộp là:
100 000 . 0,7 – 40 000 . 0,7 = 42 000 (đồng).
Số học sinh test mẫu gộp là:
420 000 : 42 000 = 10 (học sinh)
Số học sinh test mẫu đơn là:
35 – 10 = 25 (học sinh).
Vậy nếu chi phí test nhanh Covid cho 35 học sinh lớp 7A là 2 030 000 đồng thì có 25 học sinh test mẫu đơn, 10 học sinh test mẫu gộp.
