Trắc nghiệm Bài 15. Các trường hợp bằng nhau của tam giác vuông có đáp án
-
1121 lượt thi
-
15 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 1:
Khẳng định sai là
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
Các trường hợp bằng nhau của hai tam giác vuông
• Trường hợp: hai cạnh góc vuông
Nếu hai cạnh góc vuông của tam giác vuông này lần lượt bằng hai cạnh góc vuông của tam giác vuông kia thì hai tam giác vuông đó bằng nhau.
• Trường hợp: cạnh góc vuông – góc nhọn kề
Nếu một cạnh góc vuông và một góc nhọn kề cạnh ấy của tam giác vuông này bằng một cạnh góc vuông và một góc nhọn kề cạnh ấy của tam giác vuông kia thì hai tam giác vuông đó bằng nhau.
• Trường hợp: cạnh huyền – góc nhọn
Nếu cạnh huyền và một góc nhọn của tam giác vuông này bằng cạnh huyền và một góc nhọn của tam giác vuông kia thì hai tam giác vuông đó bằng nhau.
• Trường hợp: cạnh huyền – cạnh góc vuông
Nếu cạnh huyền và một cạnh góc vuông của tam giác vuông này bằng cạnh huyền và một cạnh góc vuông của tam giác vuông kia thì hai tam giác vuông đó bằng nhau.
Vậy khẳng định B sai vì phải là góc nhọn kề cạnh góc vuông mới đúng.
Câu 2:
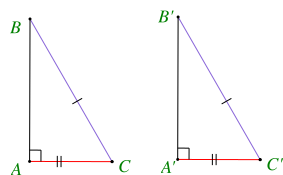
Cho hình vẽ dưới đây, khẳng định đúng là
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Xét tam giác ABC (vuông tại A) và tam giác \(A'B'C'\) (vuông tại \(A'\)) có:
\(BC = B'C'\) (cạnh huyền)
\(AC = A'C'\) (cạnh góc vuông)
Do đó: \(\Delta ABC = \Delta A'B'C'\) (cạnh huyền – cạnh góc vuông)
Câu 3:
Cho tam giác ABC vuông tại B và tam giác MNP vuông tại N, có AB = MN. Cần thêm điều kiện gì để \(\Delta ABC = \Delta MNP\) theo trường hợp hai cạnh góc vuông?
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
Vì: tam giác ABC vuông tại B và tam giác MNP vuông tại N, có AB = MN
Nên: Để \(\Delta ABC = \Delta MNP\) theo trường hợp hai cạnh góc vuông cần thêm điều kiện BC = NP. (Do AB, BC là hai cạnh góc vuông của tam giác ABC; AN, NP là hai cạnh góc vuông của tam giác MNP).
Câu 4:
Cho tam giác ABC vuông tại A và tam giác DEF vuông tại D, có AB = DE. Cần thêm điều kiện gì để \(\Delta ABC = \Delta DEF\) theo trường hợp cạnh góc vuông - góc nhọn kề?
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
Vì tam giác ABC vuông tại A và tam giác DEF vuông tại D, có AB = DE (cạnh góc vuông)
Nên để \(\Delta ABC = \Delta DEF\) theo trường hợp cạnh góc vuông - góc nhọn kề cần thêm điều kiện \(\widehat B = \widehat E\) (do góc B là góc nhọn kề với cạnh AB; góc E là góc nhọn kề với cạnh DE).
Câu 5:
Cho tam giác ABC vuông tại C và tam giác DEF vuông tại F, có \(\widehat B = \widehat E\). Cần thêm điều kiện gì để \(\Delta ABC = \Delta DEF\) theo trường hợp cạnh huyền - góc nhọn?
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
Vì tam giác ABC vuông tại C và tam giác DEF vuông tại F, có \(\widehat B = \widehat E\) (góc nhọn)
Nên để \(\Delta ABC = \Delta DEF\) theo trường hợp cạnh huyền - góc nhọn thì cần thêm điều kiện AB = DE (do tam giác ABC vuông tại C nên AB là cạnh huyền, tam giác DEF vuông tại F nên DE là cạnh huyền).
Câu 6:
Cho tam giác ABC vuông tại C và tam giác MNO vuông tại O, có BC = NO. Cần thêm điều kiện gì để \(\Delta ABC = \Delta MNO\) theo trường hợp cạnh huyền – cạnh góc vuông?
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
Vì tam giác ABC vuông tại C và tam giác MNO vuông tại O, có BC = NO (cạnh góc vuông).
Nên để \(\Delta ABC = \Delta MNO\) theo trường hợp cạnh huyền – cạnh góc vuông thì cần thêm điều kiện AB = MN (do tam giác ABC vuông tại C nên AB là cạnh huyền, tam giác MNO vuông tại O nên MN là cạnh huyền).
Câu 7:
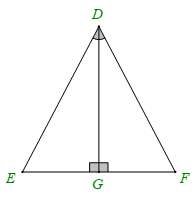
Cho hình vẽ dưới đây. Khẳng định đúng là
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
Hai tam giác DEG (vuông tại G) và tam giác DFG (vuông tại G) có:
DG là cạnh chung
\(\widehat {EDG} = \widehat {FDG}\)
Nên \(\Delta DEG = \Delta DFG\) (cạnh góc vuông – góc nhọn kề).
(Đỉnh D của hai tam giác tương ứng với nhau;
đỉnh E tương ứng với đỉnh F;
đỉnh G của hai tam giác tương ứng với nhau).
Câu 8:
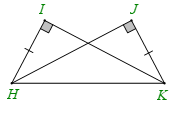
Cho hình vẽ dưới đây. Khẳng định đúng là
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
Hai tam giác HIK (vuông tại I) và tam giác KJH (vuông tại J) có:
HK là cạnh chung
HI = KJ
Nên \(\Delta HIK = \Delta KJH\) (cạnh huyền – cạnh góc vuông).
(Đỉnh H của tam giác này tương ứng với đỉnh K của tam giác kia và ngược lại; đỉnh I tương ứng với đỉnh J).
Câu 9:
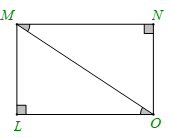
Cho hình vẽ dưới đây. Khẳng định sai là
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Hai tam giác MLO (vuông tại L) và tam giác ONM (vuông tại N) có:
MO là cạnh chung
\(\widehat {LOM} = \widehat {NMO}\)
Nên \(\Delta MLO = \Delta ONM\) (cạnh huyền – góc nhọn).
(đỉnh L tương ứng với đỉnh N, đỉnh M của tam giác này tương ứng với đỉnh O của tam giác kia và ngược lại).
Câu 10:
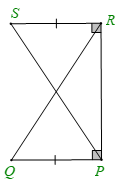
Cho hình vẽ dưới đây. Khẳng định đúng là
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
Hai tam giác SRP (vuông tại R) và tam giác QPR (vuông tại P) có:
RP là cạnh chung
SR = QP
Nên \(\Delta SRP = \Delta QPR\) (hai cạnh góc vuông).
(Đỉnh S tương ứng với đỉnh Q; đỉnh R của tam giác này tương ứng với đỉnh P của tam giác kia và ngược lại).
Câu 11:
Cho tam giác ABC vuông tại A và tam giác POI vuông tại I có BC = OP, \(\widehat C = \widehat P\). Khẳng định đúng là
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
Xét tam giác ABC vuông tại A và tam giác IOP vuông tại I có
BC = OP
\(\widehat C = \widehat P\)
Nên \(\Delta ABC = \Delta IOP\) (cạnh huyền – góc nhọn)
⇒ AB = IO (hai cạnh tương ứng)
\(\widehat B = \widehat O\) (hai góc tương ứng)
Vậy khẳng định D đúng.
Câu 12:
Cho tam giác ABC vuông tại A và tam giác PMN vuông tại P có AB = PM, AC = PN. Biết \(\widehat B = 60^\circ \). Số đo góc N là
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Xét tam giác ABC vuông tại A và tam giác PMN vuông tại P có:
AB = PM
AC = PN
Do đó: \(\Delta ABC = \Delta PMN\) (hai cạnh góc vuông)
⇒ \(\widehat B = \widehat M\) (hai góc tương ứng)
⇒ \(\widehat M = 60^\circ \)
Xét tam giác PMN vuông tại P có:
\(\widehat P + \widehat M + \widehat N = 180^\circ \) (tổng 3 góc trong tam giác)
⇒ \(90^\circ + 60^\circ + \widehat N = 180^\circ \)
⇒ \(\widehat N = 30^\circ \)
Câu 13:
Cho hình chữ nhật ABCD, M là trung điểm của cạnh CD. Khẳng định sai là

 Xem đáp án
Xem đáp án
Đáp án đúng là: B
ABCD là hình chữ nhật ⇒ AD = BC và \(\widehat {ADM} = \widehat {BCM} = 90^\circ \)
Xét tam giác ADM (vuông tại D) và tam giác BCM (vuông tại C) có:
AD = BC (chứng minh trên)
DM = CM (theo giả thiết)
⇒ \(\Delta ADM = \Delta BCM\) (hai cạnh góc vuông)
⇒ AD = BC; AM = BM (các cạnh tương ứng)
(hai góc tương ứng)
Vậy khẳng định B sai.
Câu 14:
Cho tam giác ABC vuông tại B và tam giác PMN vuông tại M có AC = PN,  . Biết AB = 4 cm; AC = 5 cm. Chu vi tam giác PMN là 12 cm. Diện tích tam giác PMN là
. Biết AB = 4 cm; AC = 5 cm. Chu vi tam giác PMN là 12 cm. Diện tích tam giác PMN là
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
AC = PN ⇒ PN = 5 cm
Xét tam giác ABC vuông tại B và tam giác PMN vuông tại M có:
AC = PN
\(\widehat A = \widehat P\)
Do đó: \(\Delta ABC = \Delta PMN\) (cạnh huyền – góc nhọn)
⇒ AB = PM (hai cạnh tương ứng)
⇒ PM = 4 cm
Chu vi tam giác PMN là:
PM + MN + PN = 12 (cm)
⇒ 4 + MN + 5 = 12
⇒ MN = 3 (cm)
Tam giác PMN vuông tại M có PM, MN là hai cạnh góc vuông nên
Diện tích tam giác PMN là: \(\frac{1}{2}PM \cdot MN = \frac{1}{2} \cdot 4 \cdot 3\) = 6 (cm2)
Câu 15:
Cho hình vẽ dưới đây, biết AB vuông góc với BC, AD vuông góc với CD và cạnh AB = AD. Khẳng định sai là

 Xem đáp án
Xem đáp án
Đáp án đúng là: D
a) Xét tam giác BAC (vuông tại B) và tam giác DAC (vuông tại D) có:
AC là cạnh chung
AB = AD (theo giả thiết)
⇒ \(\Delta BAC = \Delta DAC\) (cạnh huyền – cạnh góc vuông) (A đúng)
b) Vì \(\Delta BAC = \Delta DAC\) (theo câu a) ⇒ \(\widehat {BAC} = \widehat {DAC}\) (hai góc tương ứng) hay \(\widehat {BAH} = \widehat {DAH}\)
Xét tam giác BAH và tam giác DAH có:
AB = AD (theo giả thiết)
\(\widehat {BAH} = \widehat {DAH}\) (chứng minh trên)
AH là cạnh chung
⇒ \(\Delta BAH = \Delta DAH\) (c.g.c) (B đúng)
⇒ \(\widehat {AHB} = \widehat {AHD}\) (hai góc tương ứng)
Mà \(\widehat {AHB} + \widehat {AHD} = 180^\circ \) (hai góc kề bù)
Nên \(\widehat {AHB} = \widehat {AHD} = 90^\circ \)
⇒ AC ⊥ BD (đpcm). (C đúng)
Khẳng định D sai.
