Trắc nghiệm bài tập theo tuần Toán 7- Tuần 26 có đáp án
-
334 lượt thi
-
11 câu hỏi
-
45 phút
Danh sách câu hỏi
Câu 1:
Trong các biểu thức sau ( là các biến) biểu thức nào là đơn thức. Với mỗi đơn thức tìm được hãy chỉ rõ hệ số, phần biến và tìm bậc của đơn thức đó:
 Xem đáp án
Xem đáp án
Hệ số: , biến: , bậc: 4
Câu 2:
Thu gọn các đơn thức sau, xác định hệ số và phần biến, bậc của đơn thức sau khi thu gọn:
 Xem đáp án
Xem đáp án
Hệ số: 2, phần biến: , bậc của đơn thức: 10.
Câu 3:
Thu gọn các đơn thức sau, xác định hệ số và phần biến, bậc của đơn thức sau khi thu gọn:
 Xem đáp án
Xem đáp án
Hệ số: 30, phần biến: , bậc của đơn thức: 35 .
Câu 4:
Thu gọn các đơn thức sau, xác định hệ số và phần biến, bậc của đơn thức sau khi thu gọn:
 Xem đáp án
Xem đáp án
Hệ số: 8, phần biến: , bậc của đơn thức: 23
Câu 5:
 Xem đáp án
Xem đáp án
Tổng các đơn thức trong mỗi nhóm trên là:
Câu 6:
Tính các tổng và hiệu dưới đây tồi viết chữ tương ứng vào các ô trông, ta sẽ được tên một nhạc sĩ lừng danh người Ba Lan.
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
 Xem đáp án
Xem đáp án
HS tự tính toán và điền được kết quả:
|
|
0 |
|
|
|
|
|
C |
H |
O |
P |
I |
N |
Vậy nhạc sĩ người Ba Lan đó là: Chopin
Frédéric François Chopin (phiên âm: Phơ-rê-đê-rích Sô-panh) ( /ˈʃoʊpæn/; tiếng Pháp: [fʁedeʁik fʁɑ̃swa ʃɔpɛ̃]; tên khai sinh Fryderyk Franciszek Chopin,[gc 1] 1 tháng 3 năm 1810 – 17 tháng 10 năm 1849) là nhà soạn nhạc và nghệ sĩ dương cầm người Ba Lan của thời kỳ âm nhạc Lãng mạn. Ông nổi tiếng toàn thế giới như một trong những người đi tiên phong của thời kỳ này "với chất thơ thiên tài đi cùng với kỹ thuật không một ai đương thời có thể sánh bằng"[1]. Chopin sinh ra tại Công quốc Warszawa và lớn lên chủ yếu ở thành phố Warsaw, sau này trở thành một phần của Vương quốc Lập hiến Ba Lan vào năm 1815. Chopin sớm nổi tiếng là thần đồng, và ông được đào tạo âm nhạc và văn hóa xuất sắc trước khi rời khỏi Ba Lan vào năm 20 tuổi.

Câu 9:
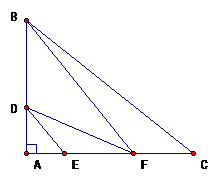
Ở hình 2 so sánh ABvà KN (có giải thích).
 Xem đáp án
Xem đáp án
Vì A nằm giữa M và K nên (qh giữa hình chiếu và đường xiên)
Câu 10:
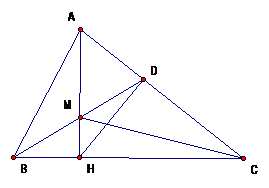
Cho nhọn, Lấy điểm M nằm giữa A,H (AH là đường cao), tia BM cắt AC ở D Chứng minh
và
 Xem đáp án
Xem đáp án
Vì nên (qh đường xiên và
hình chiếu)
(qh hình chiếu và đường xiên) (đpcm).
Câu 11:
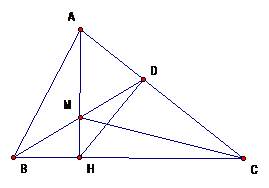
Cho nhọn, Lấy điểm M nằm giữa A,H (AH là đường cao), tia BM cắt AC ở D Chứng minh
DM<DH
 Xem đáp án
Xem đáp án
Xét vuông tại H có là góc nhọn
suy ra là góc tù
( qh giữa cạnh và góc đối diện trong
tam giác).(đpcm)