16 câu hỏi trắc nghiệm thuộc Trắc nghiệm bài tập theo tuần Toán 7-Tuần 27 có đáp án

Câu 1:

Tìm bậc của các đa thức sau:

$A = 6 x^{4} - 5 x^{2} + 4 x - 3 x^{4} + 2 x^{3}$

Xem đáp án

$A = 6 x^{4} - 5 x^{2} + 4 x - 3 x^{4} + 2 x^{3} = 3 x^{4} - 5 x^{2} + 4 x + 2 x^{3}$

Bậc của đa thức là 4

Câu 2:

Tìm bậc của các đa thức sau:

$B = - 5 x^{3} y^{2} + 4 x^{2} y^{2} - x^{3} + 8 x^{2} y^{2} + 5 x^{3} y^{2}$

Xem đáp án

$B = - 5 x^{3} y^{2} + 4 x^{2} y^{2} - x^{3} + 8 x^{2} y^{2} + 5 x^{3} y^{2} = 12 x^{2} y^{2} - x^{3}$

Bậc của đa thức là 4

Câu 3:

Tìm bậc của các đa thức sau:

$C = \frac{1}{2} x^{4} y^{4} + 6 x^{6} + \frac{1}{2} x^{4} y^{4} - 5 x^{4} y^{3} - x^{4} y^{4}$

Xem đáp án

$C = \frac{1}{2} x^{4} y^{4} + 6 x^{6} + \frac{1}{2} x^{4} y^{4} - 5 x^{4} y^{3} - x^{4} y^{4} = 6 x^{6} - 5 x^{4} y^{3}$

Bậc của đa thức là 7

Câu 4:

Tìm bậc của các đa thức sau:

$D = 3 x^{2} y - \frac{1}{4} x y + 1 - 3 x^{2} y + \frac{1}{2} x y - \frac{1}{4} x y$

Xem đáp án

$D = 3 x^{2} y - \frac{1}{4} x y + 1 - 3 x^{2} y + \frac{1}{2} x y - \frac{1}{4} x y = 1$

Bậc của đa thức là 0

Câu 5:

Cho các đa thức

$A = 5 x^{3} y - 4 x y^{2} - 6 x^{2} y^{2}$

Xem đáp án

$A - B - C$

= (5 x^{3} y - 4 x y^{2} - 6 x^{2} y^{2}) - (- 8 x y^{3} + x y^{2} - 4 x^{2} y^{2}) - (x^{3} + 4 x^{3} y - 6 x y^{3} - 4 x y^{2} + 5 x^{2} y^{2})

= 5 x^{3} y - 4 x y^{2} - 6 x^{2} y^{2} + 8 x y^{3} - x y^{2} + 4 x^{2} y^{2} - x^{3} - 4 x^{3} y + 6 x y^{3} + 4 x y^{2} - 5 x^{2} y^{2}

= x^{3} y - x y^{2} - 7 x^{2} y^{2} + 14 x y^{3} - x^{3}

Câu 6:

Cho các đa thức $B = - 8 x y^{3} + x y^{2} - 4 x^{2} y^{2}$

Xem đáp án

$B + A - C$

$= (- 8 x y^{3} + x y^{2} - 4 x^{2} y^{2}) + (5 x^{3} y - 4 x y^{2} - 6 x^{2} y^{2}) - (x^{3} + 4 x^{3} y - 6 x y^{3} - 4 x y^{2} + 5 x^{2} y^{2})$ $= - 8 x y^{3} + x y^{2} - 4 x^{2} y^{2} + 5 x^{3} y - 4 x y^{2} - 6 x^{2} y^{2} - x^{3} - 4 x^{3} y + 6 x y^{3} + 4 x y^{2} - 5 x^{2} y^{2}$

$= - 2 x y^{3} + x y^{2} - 15 x^{2} y^{2} + x^{3} y - x^{3}$

Câu 7:

Cho các đa thức $C = x^{3} + 4 x^{3} y - 6 x y^{3} - 4 x y^{2} + 5 x^{2} y^{2}$

$C - A - B$

Xem đáp án

$C - A - B$

= (x^{3} + 4 x^{3} y - 6 x y^{3} - 4 x y^{2} + 5 x^{2} y^{2}) - (5 x^{3} y - 4 x y^{2} - 6 x^{2} y^{2}) - (- 8 x y^{3} + x y^{2} - 4 x^{2} y^{2})

$= x^{3} + 4 x^{3} y - 6 x y^{3} - 4 x y^{2} + 5 x^{2} y^{2} - 5 x^{3} y + 4 x y^{2} + 6 x^{2} y^{2} + 8 x y^{3} - x y^{2} + 4 x^{2} y^{2}$

$= x^{3} - x^{3} y + 2 x y^{3} - x y^{2} + 15 x^{2} y^{2}$

Câu 8:

Tìm các đa thức $M, N$ biết:

$M + 2 x y^{2} - 3 x^{2} y + 4 x y = - 2 x^{2} y + x y^{2} - 4 x + 4 x y$

Xem đáp án

$M = x^{2} y - x y^{2} - 4 x$

Câu 9:

Tìm các đa thức $M, N$ biết: $N - (2 x y + 3 x y^{3} - x^{2} y^{2}) + 2 x^{2} y = 5 x y - 2 x^{2} y^{2} + 3 x^{2} y - y^{3}$

Xem đáp án

$N = - 3 x^{2} y^{2} + 3 x y^{3} + x^{2} y + 7 x y - y^{3}$

Câu 10:

Tính giá trị của các đa thức sau:

x y + x^{2} y^{2} + x^{3} y^{3} + x^{4} y^{4} + \dots + x^{2004} y^{2004}

tại

x = 1; y = - 1

Xem đáp án

Tại x=1,y=-1 thì

x y + x^{2} y^{2} + x^{3} y^{3} + x^{4} y^{4} + \dots + x^{2004} y^{2004} = - 1 + 1 - 1 + 1 - \dots + 1 = 0

Câu 11:

Tính giá trị của các đa thức sau:

$6 x - 12 (y + 2) + 6 y$ biết $x = y - 1$

Xem đáp án

Khi biết $x = y - 1$ ta có:

6 x - 12 (y + 2) + 6 y = 6 (y - 1) - 12 (y + 2) + 6 y = - 30

Câu 12:

Tính giá trị của các đa thức sau:

$A = x^{3} - x^{2} y + 3 x^{2} - x y + y^{2} - 4 y + x + 2$ biết $x - y + 3 = 0$

Xem đáp án

A = x^{3} - x^{2} y + 3 x^{2} - x y + y^{2} - 4 y + x + 2

= x^{2} (x - y + 3) - y (x - y + 3) - y + x + 2

= x^{2} (x - y + 3) - y (x - y + 3) + (x - y + 3) - 1

= (x - y + 3) (x^{2} - y + 1) - 1

Nên với $x - y + 3 = 0$ suy ra $A = 0 - 1 = - 1.$

Câu 13:

Hãy lựa 3 số trong những số cho sau đây sao cho đó là độ dài 3 cạnh của một tam giác. Gạch dưới những bộ ba là độ dài 3 cạnh một tam giác vuông:

3; 4; 5; 6; 8; 10.

Xem đáp án

Bộ 3 số trong những số là độ dài 3 cạnh của một tam giác là:

(3,4,5) vì 5 < 3 + 4	(3,4,6) vì 6 < 3 + 4	(3,8,10) vì 10 < 3 + 8
(3,5,6) vì 6 < 3 + 5	(3,6,8) vì 8 < 3 + 6
(4,5, 6) vì 6 < 4 + 5	(4,5, 8) vì 8 < 4 + 5	(4,6, 8) vì 8 < 4 + 6	(4,8, 10) vì 10 < 4 + 8
(5, 6, 8) vì 8 < 6 + 5	(5, 6, 10) vì 10 < 6 + 5	(5, 8, 10) vì 10 < 8 + 5
vì 10 < 6 + 8(6, 8,10)

* những bộ ba là độ dài 3 cạnh một tam giác vuông: (3,4,5) ;(10, 6, 8)

Câu 14:

Cho $Δ A B C$ cân.

Tính $A C, B C$ biết chu vi $Δ A B C$ là $23 c m$ và $A B = 5 c m$ .

Xem đáp án

Tính $A C, B C$ biết chu vi $Δ A B C$ là 23 cm và $A B = 5 c m .$

* Nếu $A B$ là cạnh bên và $Δ A B C$ cân tại $A$

$\Rightarrow A B = A C = 5 c m .$

$\Rightarrow B C = 13 c m$ (không t/m BĐT tam giác).

* Nếu AB là cạnh bên và $Δ A B C$ cân tại B

$\Rightarrow A B = B C = 5 c m .$

$\Rightarrow A C = 13 c m$ ( không t/m BĐT tam giác).

*Nếu AB là cạnh đáy thì $Δ A B C$ cân tại C

$\Rightarrow A C = B C = (23 - 5) : 2 = 9 c m .$ (thỏa mãn BĐT tam giác)

Vậy: $A C = B C = 9 c m .$

Câu 15:

Cho

Δ A B C

cân.

Tính chu vi $Δ A B C$ biết $A B = 5 c m, A C = 12 c m$ .

Xem đáp án

Tính chu vi $Δ A B C$ biết $A B = 5 c m, A C = 12 c m .$

* Nếu $A B = B C = 5 c m$ là cạnh bên

$\Rightarrow A C = 12 c m$ là cạnh đáy

Khi đó $12 > 5 + 5$ ( không thỏa mãn BĐT tam giác).

Vậy $A C = B C = 12 c m$ là cạnh bên

$A B = 5 c m$ là cạnh đáy

Chu vi $Δ A B C$ là : $12 + 12 + 5 = 29$ (cm)

Câu 16:

Cho $Δ A B C$ có $(A B < A C)$ và $A D$ là phân giác góc $A (D \in B C)$ . Gọi E là một điểm

bất kỳ thuộc cạnh $A D (E$ khác A). Chứng minh $A C - A B > E C - E B$ .

Xem đáp án

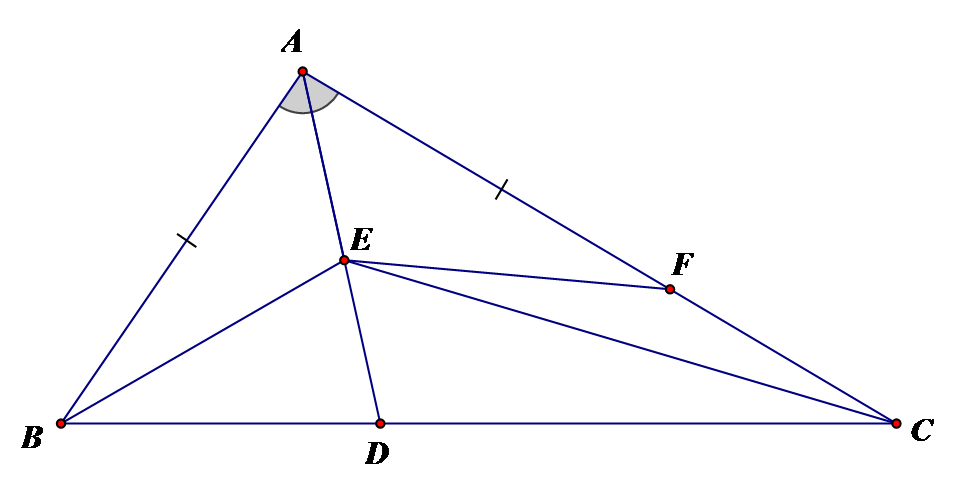
Trên cạnh $A C$ lấy điểm F sao cho $A F = A B .$ Xét $Δ A B E$ và $Δ A F E$ có $A B = A F,$ $\hat{B A E} = \hat{F A E};$ $A E$ chung . Do đó $Δ A B E = Δ A F E$ (c.g.c) $\Rightarrow B E = E F .$

Trong tam giác $E F C$ có $F C > E C - E F$ mà $B E = E F$ nên $F C > E C - E B$ (1)

Lại có $F C = A C - A F$ mà $A F = A B$ nên $F C = A C - A B$ (2)

Từ (1) và (2) suy ra $A B - A C > E C - E B .$