Trắc nghiệm Toán 7 Bài tập cuối tập chương 4 có đáp án (Nhận biết)
-
960 lượt thi
-
7 câu hỏi
-
15 phút
Danh sách câu hỏi
Câu 1:
Quan sát hình vẽ.
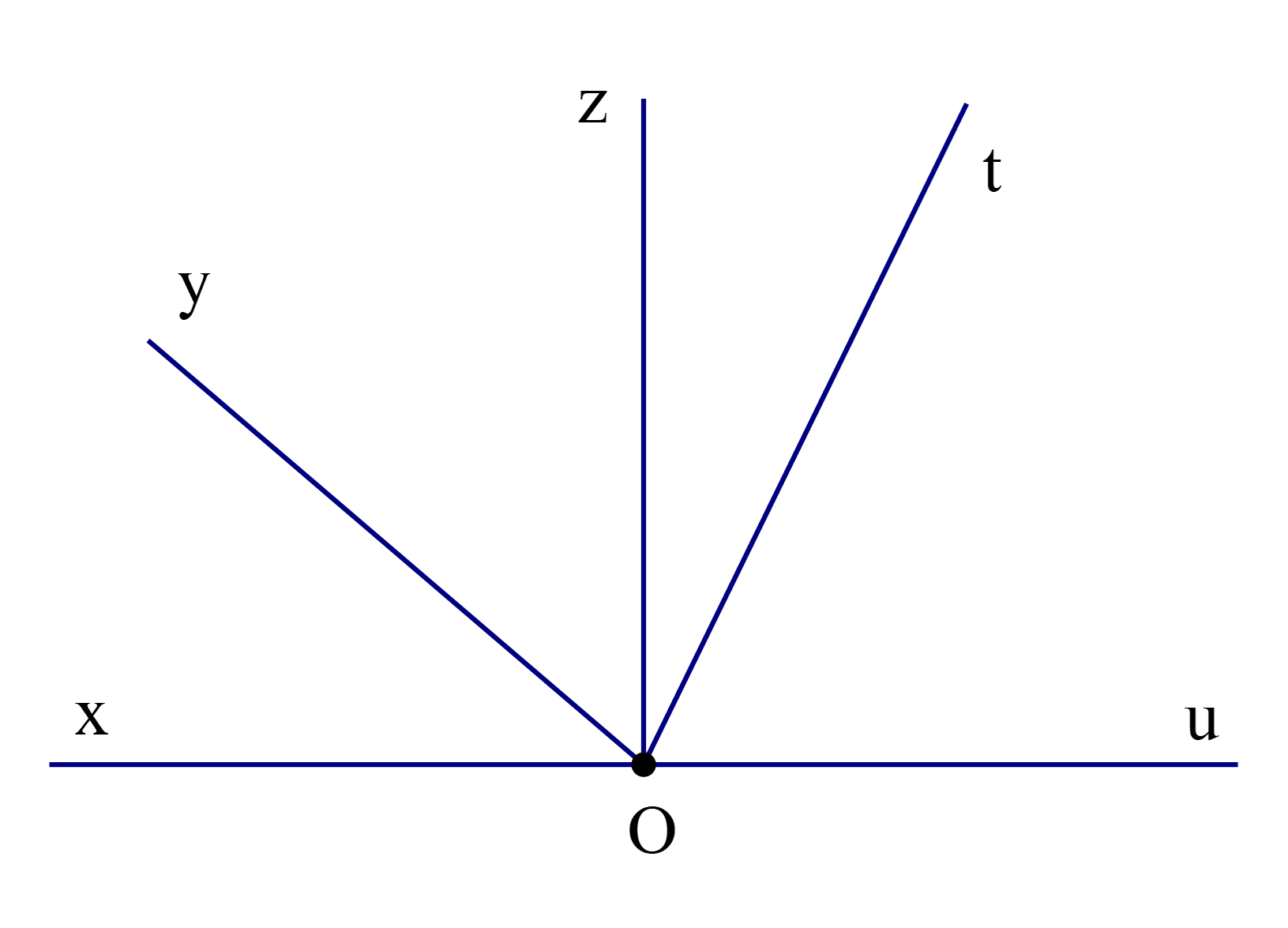
Có tất cả bao nhiêu góc kề (không kể góc bẹt) với \(\widehat {{\rm{xOy}}}\)?
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: C
Hai góc kề nhau là hai góc có một cạnh chung và không có điểm trong chung.
Do đó các góc kề với \(\widehat {{\rm{xOy}}}\)là: \(\widehat {{\rm{yOz}}}{\rm{; }}\widehat {{\rm{yOt}}}{\rm{; }}\widehat {{\rm{yOu}}}.\)
Vậy có tất cả 3 góc kề (không kể góc bẹt) với \(\widehat {{\rm{xOy}}}\).
Vậy ta chọn phương án C.
Câu 2:
Cho hình vẽ
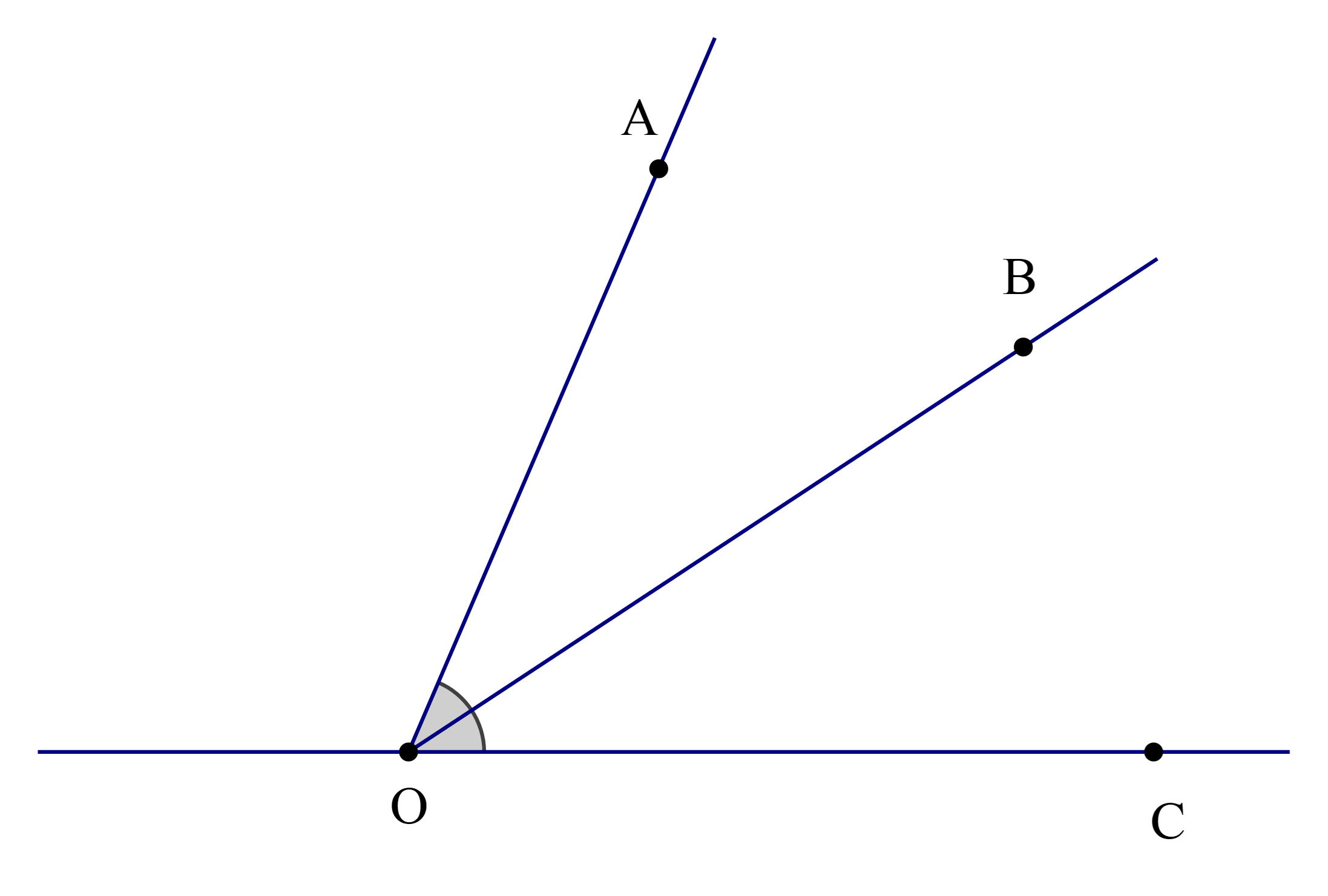
Chọn khẳng định đúng:
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: B
Vì tia OB nằm giữa hai tia OA và OC nên tạo thành hai góc tương ứng là \(\widehat {{\rm{AOB}}}\) và \(\widehat {{\rm{BOC}}}.\)
Mà \(\widehat {{\rm{AOB}}} = \widehat {{\rm{BOC}}}.\)
Do đó OB là tia phân giác của \(\widehat {{\rm{AOC}}}.\)
Vậy ta chọn phương án B.
Câu 3:
Tia Oz là tia phân giác của \(\widehat {{\rm{xOy}}}\), biết rằng \(\widehat {{\rm{xOz}}} = 40^\circ \). Số đo của \(\widehat {{\rm{yOz}}}\) là:
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: B
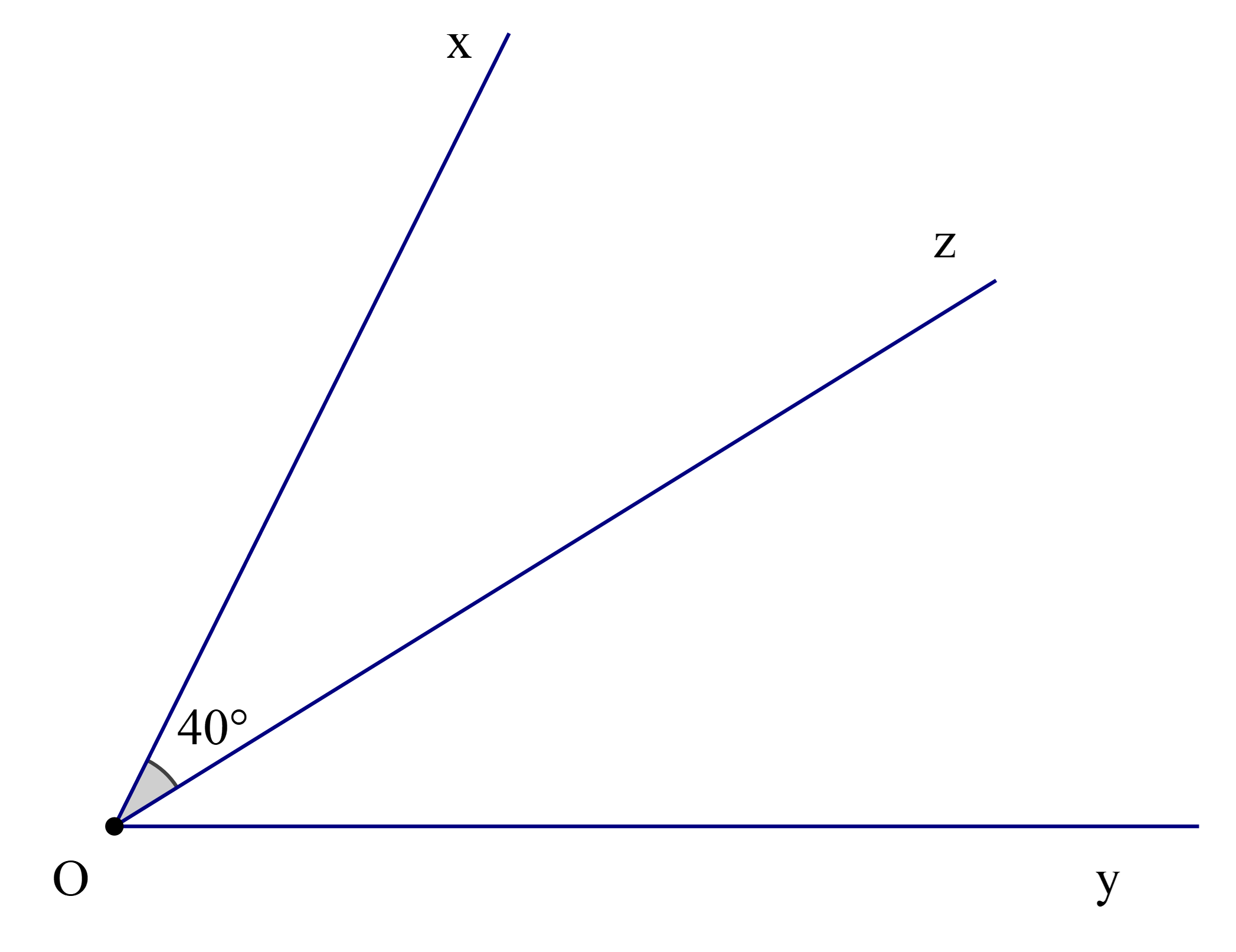
Theo bài ta có: Oz là tia phân giác của \(\widehat {{\rm{xOy}}}\)
Nên \(\widehat {{\rm{xOz}}} = \widehat {{\rm{zOy}}}\) (tính chất tia phân giác của một góc)
Mà \(\widehat {{\rm{xOz}}} = 40^\circ \)
Suy ra \(\widehat {{\rm{yOz}}} = 40^\circ \)
Vậy ta chọn phương án B.
Câu 4:
Cho \(\widehat {{\rm{DOF}}} = 140^\circ \), biết rằng OE là tia phân giác của \(\widehat {{\rm{DOF}}}\). Số đo của \(\widehat {EOF}\) là
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: C
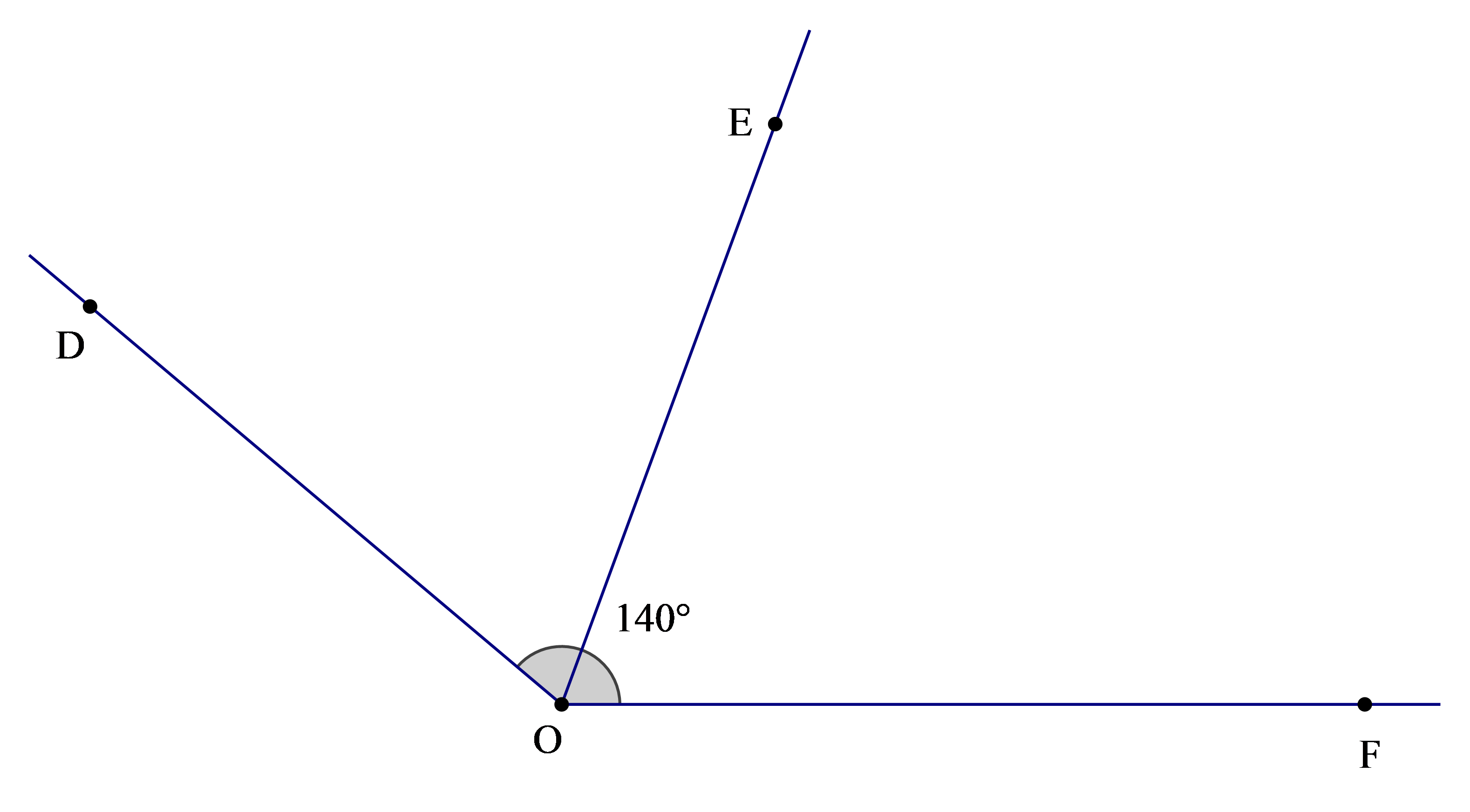
Theo bài ta có: OE là tia phân giác của \(\widehat {{\rm{DOF}}}\)
Nên \(\widehat {{\rm{DOE}}} = \widehat {EOF}\) (tính chất đường phân giác của một góc) (1)
Ta lại có \(\widehat {{\rm{DOE}}} + \widehat {EOF} = \widehat {{\rm{DOF}}}\) (hai góc kề nhau) (2)
Từ (1) và (2) suy ra \(\widehat {{\rm{DOE}}} = \widehat {EOF} = \frac{1}{2}\widehat {{\rm{DOF}}} = \frac{1}{2}.140^\circ = 70^\circ \)
Do đó \(\widehat {EOF} = 70^\circ \)
Vậy ta chọn phương án C.
Câu 5:
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: D
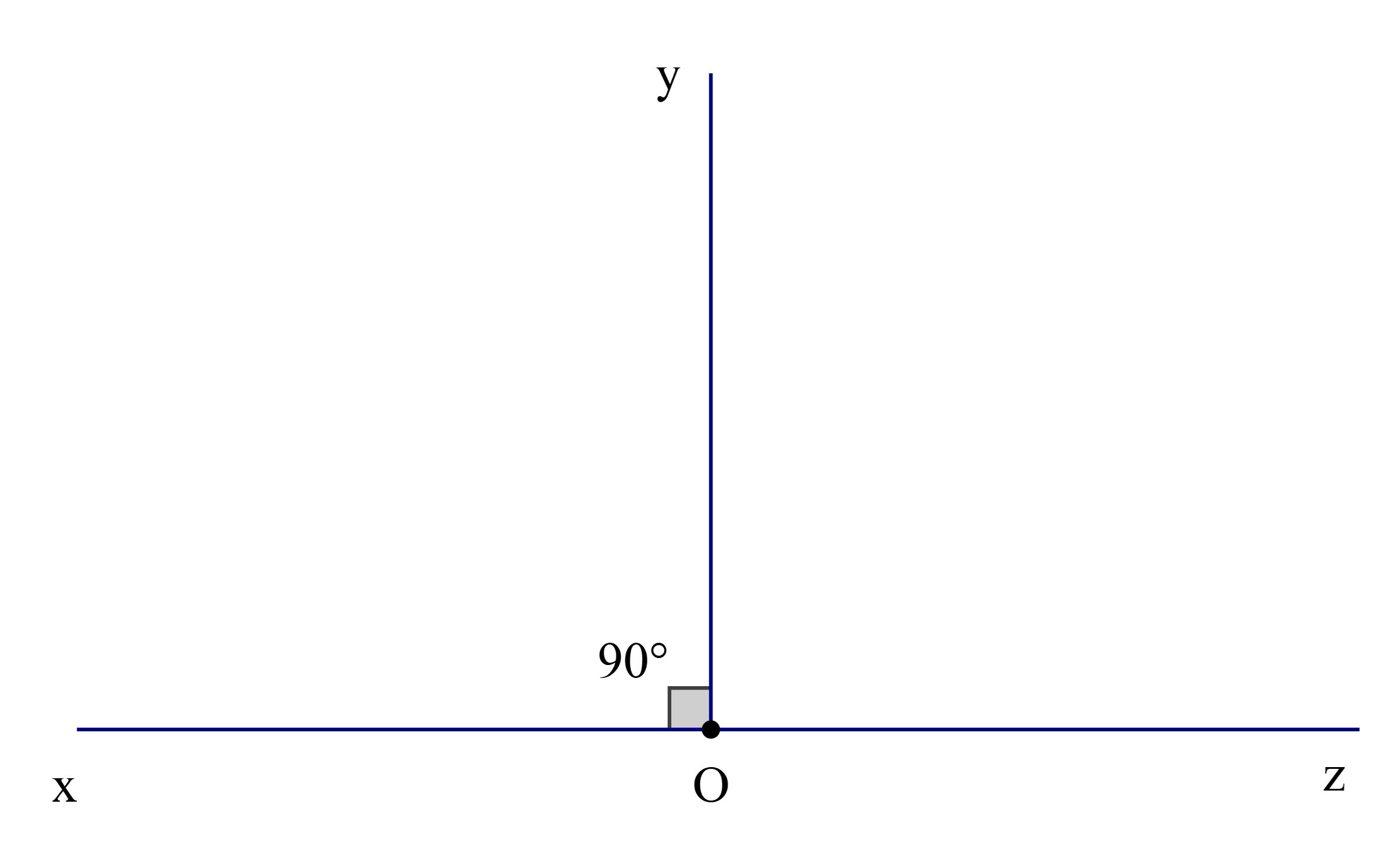
Theo bài tia Oy là phân giác của \(\widehat {xOz}\)
Nên \(\widehat {{\rm{yOz}}} = \widehat {{\rm{xOy}}} = 90^\circ \)(tính chất tia phân giác của một góc)
Ta có \(\widehat {{\rm{xOy}}} + \widehat {{\rm{yOz}}} = \widehat {{\rm{xOz}}}\) (hai góc kề nhau)
Hay \(90^\circ + 90^\circ = \widehat {{\rm{xOz}}}\)
Suy ra \(\widehat {{\rm{xOz}}} = 180^\circ \)
Do đó \(\widehat {{\rm{xOz}}}\) là góc bẹt
Vậy ta chọn phương án D.
Câu 6:
Cho a // b, đường thẳng c cắt hai đường thẳng a, b lần lượt tại E và F sao cho \(\widehat {{\rm{MEF}}} = 80^\circ \).
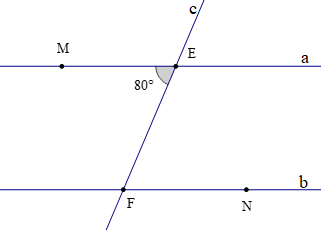
Số đo \(\widehat {EFN}\)là
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: B
Theo bài ta có a // b mà \(\widehat {{\rm{MEF}}}\) và \(\widehat {EFN}\) là hai góc ở vị trí so le trong.
Do đó \(\widehat {{\rm{MEF}}} = \widehat {EFN}\) (tính chất của hai đường thẳng song song)
Mà \(\widehat {{\rm{MEF}}} = 80^\circ \) nên \(\widehat {EFN} = 80^\circ \)
Vậy ta chọn phương án B.
Câu 7:
Cho định lí: “Hai đường thẳng phân biệt cùng vuông góc với một đường thẳng thứ ba thì chúng song song với nhau”. Giả thiết của định lí là
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: B
Định lí “Hai đường thẳng phân biệt cùng vuông góc với một đường thẳng thứ ba thì chúng song song với nhau” là một định lí có:
+ Giả thiết: hai đường thẳng phân biệt cùng vuông góc với một đường thẳng thứ ba;
+ Kết luận: chúng song song với nhau.
Do đó A, C, D sai ; B đúng
Vậy ta chọn phương án B.