Trắc nghiệm Toán 7 CD Bài 9. Đường trung trực của một đoạn thẳng (Phần 2) có đáp án
Trắc nghiệm Toán 7 CD Bài 9. Đường trung trực của một đoạn thẳng (Vận dụng) có đáp án
-
458 lượt thi
-
3 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 1:
Cho tam giác ABC cân tại A có AH là đường phân giác của góc BAC (H ∈ BC). Khẳng định sai là
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: D
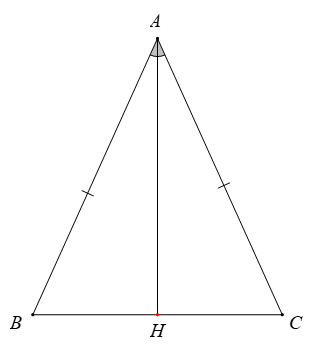
Xét tam giác ABH và tam giác ACH có:
AB = AC (∆ABC cân tại A)
(AH là đường phân giác của )
AH là cạnh chung
Do đó, ∆ABH = ∆ACH (c.g.c)
⇒ HB = HC (hai cạnh tương ứng) (1)
Và (hai góc tương ứng)
Mà (hai góc kề bù)
⇒⇒ AH ⊥ BC (2)
Từ (1) và (2) ⇒AH là đường trung trực của đoạn thẳng BC.
Câu 2:
Cho M, N là hai điểm phân biệt nằm trên đường trung trực của cạnh AB sao cho AM = BN. O là giao điểm của MN và AB. Khẳng định sai là
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: C
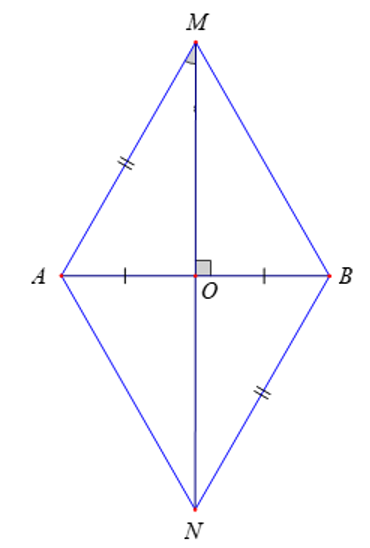
MN là đường trung trực của AB ⇒ MN ⊥ AB tại O và OA = OB
+) Xét hai tam giác vuông AMO và BNO có:
AM = BN (theo giả thiết)
OA = OB
⇒ ∆AMO = ∆BNO (cạnh huyền – cạnh góc vuông)
+) Ta có: AN = BN (vì N thuộc đường trung trực của AB) ⇒ ∆ANB cân tại N.
Mà AM = BN (theo giả thiết)
⇒ AN = AM
⇒ ∆AMN cân tại A (đpcm)
+) Có: MA = MB (vì M thuộc đường trung trực của AB)
⇒ ∆AMB là tam giác cân tại M.
Câu 3:
Cho ∆ABC (AB < AC). Đường trung trực của BC cắt BC tại E và cắt AC tại F. Lấy điểm M bất kỳ trên đường thẳng d (M ≠ F). So sánh chu vi ∆AFB và chu vi ∆AMB đúng là
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: A
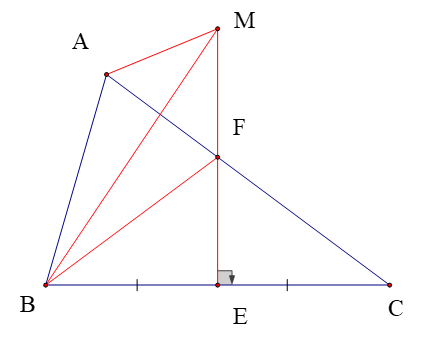
Ta có: FE là đường trung trực của BC (giả thiết)
⇒ FB = FC (tính chất đường trung trực)
M thuộc đường trung trực của BC ⇒ MB = MC (tính chất đường trung trực)
Chu vi ∆AFB = AB + AF + FB = AB + AF + FC = AB + AC
Chu vi ∆AMB = AB + AM + MB = AB + AM + MC
Xét ∆AMC có: AM + MC > AC (bất đẳng thức tam giác)
Do đó: AB + AC < AB + AM + MC
Hay chu vi ∆AFB nhỏ hơn chu vi ∆AMB.