Đề kiểm tra 15 phút Toán 7 Chương 3 Hình học có đáp án (phần Cddqctg - Trắc nghiệm - Tự luận 4)
-
18041 lượt thi
-
6 câu hỏi
-
50 phút
Danh sách câu hỏi
Câu 1:
A. Phần trắc nghiệm (4 điểm)
Trong mỗi câu dưới đây, hãy chọn phương án trả lời đúng:
Cho tam giác ABC vuông tại A, AI là tia phân giác của góc A. Khi đó số đo góc (BAI) là:
Xem đáp án
Vì AI là tia phân giác của góc A nên ∠(BAI) = 90o : 2 = 45o. Chọn B
Câu 2:
Cho tam giác ABC, điểm M nằm trên trong tam giác ABC sao cho MA = MB. Khẳng định nào sau đây đúng về vị trí điểm M
Xem đáp án
Chọn D
Câu 3:
Cho tam giác ABC có AH là đường cao kẻ từ A. Biết góc B bằng . Khi đó số đo góc (BAH) là:
Xem đáp án
Trong tam giác BAH có ∠(BAH) + ∠(AHB) + ∠(ABH) = 180o
⇒∠(BAH) = 180o - 90o - 50o = 40o
Chọn A
Câu 4:
Cho tam giác ABC có đường phân giác của góc B và C cắt nhau tại P. Khi đó AP là:
Xem đáp án
Chọn A
Câu 5:
B. Phần tự luận (6 điểm)
Cho tam giác MNP có hai đường cao MQ và NH cắt nhau tại I. Biết
a. Tính (MPN)
Xem đáp án
a. Hình vẽ ( 1 điểm)
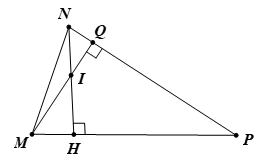
Do (MIN) là góc ngoài của tam giác MIH nên
∠(MIN) = ∠(QMH) + ∠(MHI) ( 1 điểm)
⇒∠(QMH) = ∠(MIN) - ∠(MHI) = 120o - 90o = 30o ( 1 điểm)
Trong tam giác MPQ có ∠(MPQ) + ∠(MQP) + ∠(PMQ) = 180o
Nên ∠(MPQ) = 180o - 30o - 90o = 60o ( 1 điểm)
Câu 6:
Cho tam giác MNP có hai đường cao MQ và NH cắt nhau tại I. Biết
b. Với góc P vừa tính được trong câu a và giả sử góc So sánh các cạnh của tam giác MNP
Xem đáp án
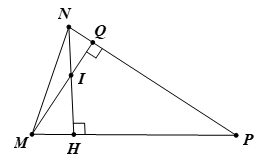
b. Với ∠(MPQ) = 60o, ∠(NMP) = 60o thì tam giác MNP cân tại N và có 1 góc bẳng 60o nên tam giác ABC là tam giác đều ( 1 điểm)
Suy ra AB = BC = AC ( 1 điểm)