Trắc nghiệm Toán 8 CTST Bài 1. Góc và cạnh của một tam giác có đáp án (Phần 2) (Nhận biết)
-
518 lượt thi
-
12 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 1:
Tổng số đo ba góc của một tam giác là
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: D
Theo định lí: Tổng số đo ba góc của một tam giác bằng 180°.
Vậy ta chọn phương án D.
Câu 2:
Chọn khẳng định đúng:
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: C
Tam giác có 3 góc nhọn được gọi là tam giác nhọn.
Vậy ta chọn phương án C.
Câu 3:
Điền vào chỗ trống: “Trong một tam giác, độ dài một cạnh bao giờ cũng lớn hơn … và nhỏ hơn … độ dài của hai cạnh còn lại”.
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: B
“Trong một tam giác, độ dài một cạnh bao giờ cũng lớn hơn hiệu và nhỏ hơn tổng độ dài của hai cạnh còn lại”
Do đó các cụm từ cần điền vào chỗ trống lần lượt là: hiệu, tổng.
Vậy ta chọn phương án B.
Câu 4:
Trong tam giác vuông, góc đối diện với cạnh huyền là
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: B
Vì trong tam giác vuông góc đối diện với cạnh huyền là góc vuông và góc đối diện với các cạnh góc vuông là các góc nhọn.
Do đó B đúng
Vậy ta chọn phương án B.
Câu 5:
Cho ∆ABC có AB > BC > AC. Chọn khẳng định sai:
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: A
Ta có “Trong một tam giác, độ dài một cạnh bao giờ cũng lớn hơn hiệu độ dài của hai cạnh còn lại”.
Do đó AB > BC – AC, nên B đúng;
AC > AB – BC, nên C đúng.
Ta lại có “Trong một tam giác, độ dài một cạnh bao giờ cũng nhỏ hơn tổng độ dài của hai cạnh còn lại”.
Do đó AC < AB + BC, nên D đúng;
AB < BC – AC, nên A sai.
Vậy ta chọn phương án A.
Câu 6:
Sau khi đo bằng thước đo góc bạn An đã điền số đo các góc vào hai hình vẽ như sau:
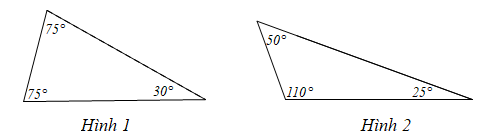
Chọn khẳng định đúng:
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: A
Xét Hình 1: Ta có \(\widehat {\rm{A}} + \widehat {\rm{B}} + \widehat {\rm{C}} = 75^\circ + 75^\circ + 30^\circ = 180^\circ \).
Xét Hình 2: Ta có \(\widehat {\rm{D}} + \widehat {\rm{E}} + \widehat {\rm{F}} = 50^\circ + 110^\circ + 25^\circ = 185^\circ \).
Mà tổng số đo ba góc của một tam giác bằng 180°.
Vậy bạn An đã đo đúng Hình 1 và đo nhầm Hình 2.
Vậy ta chọn phương án A.
Câu 7:
Trong các bộ ba độ dài đoạn thẳng dưới đây, bộ ba có thể là độ dài ba cạnh của một tam giác là
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: C
Ta có “Trong một tam giác, độ dài một cạnh bao giờ cũng lớn hơn hiệu và nhỏ hơn tổng độ dài của hai cạnh còn lại”
Vì 6 cm < 2 cm + 3 cm = 5 cm, nên A sai;
8 cm = 4 cm + 4 cm, nên B sai;
8 cm = 5 cm + 3 cm, nên D sai;
7 cm – 5 cm < 9 cm < 7 cm + 5 cm, nên C đúng.
Vậy ta chọn phương án C.
Câu 8:
Cho hình vẽ
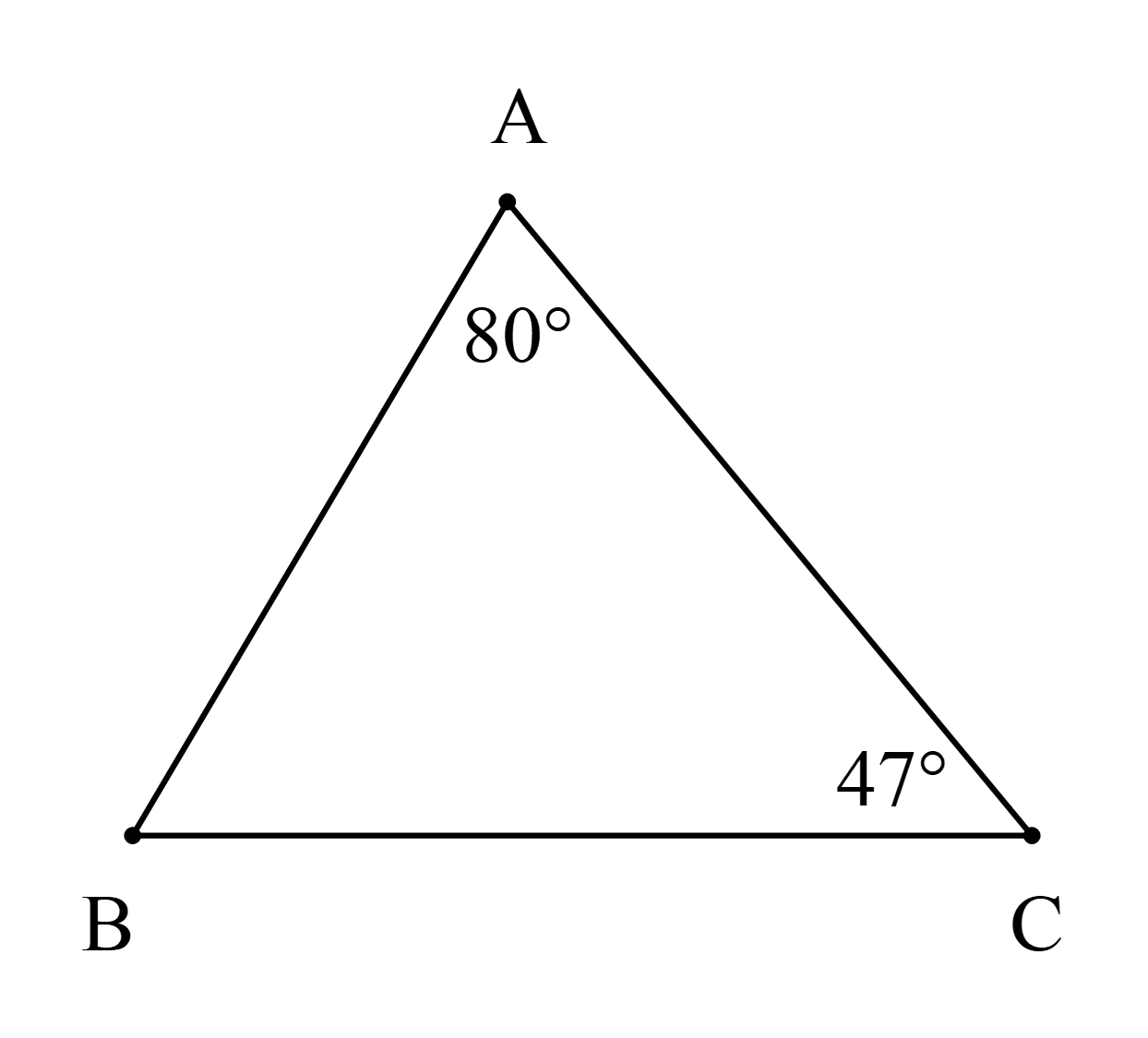
Số đo của \(\widehat {\rm{B}}\) là
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: B
Xét ∆ABC có: \(\widehat {\rm{A}} + \widehat {\rm{B}} + \widehat {\rm{C}} = 180^\circ \) (tổng ba góc trong một tam giác bằng 180°)
Hay \(80^\circ + \widehat {\rm{B}} + 47^\circ = 180^\circ \)
Suy ra \(\widehat {\rm{B}} = 180^\circ - 80^\circ - 47^\circ = 53^\circ \).
Vậy ta chọn phương án B.
Câu 9:
Cho hình vẽ
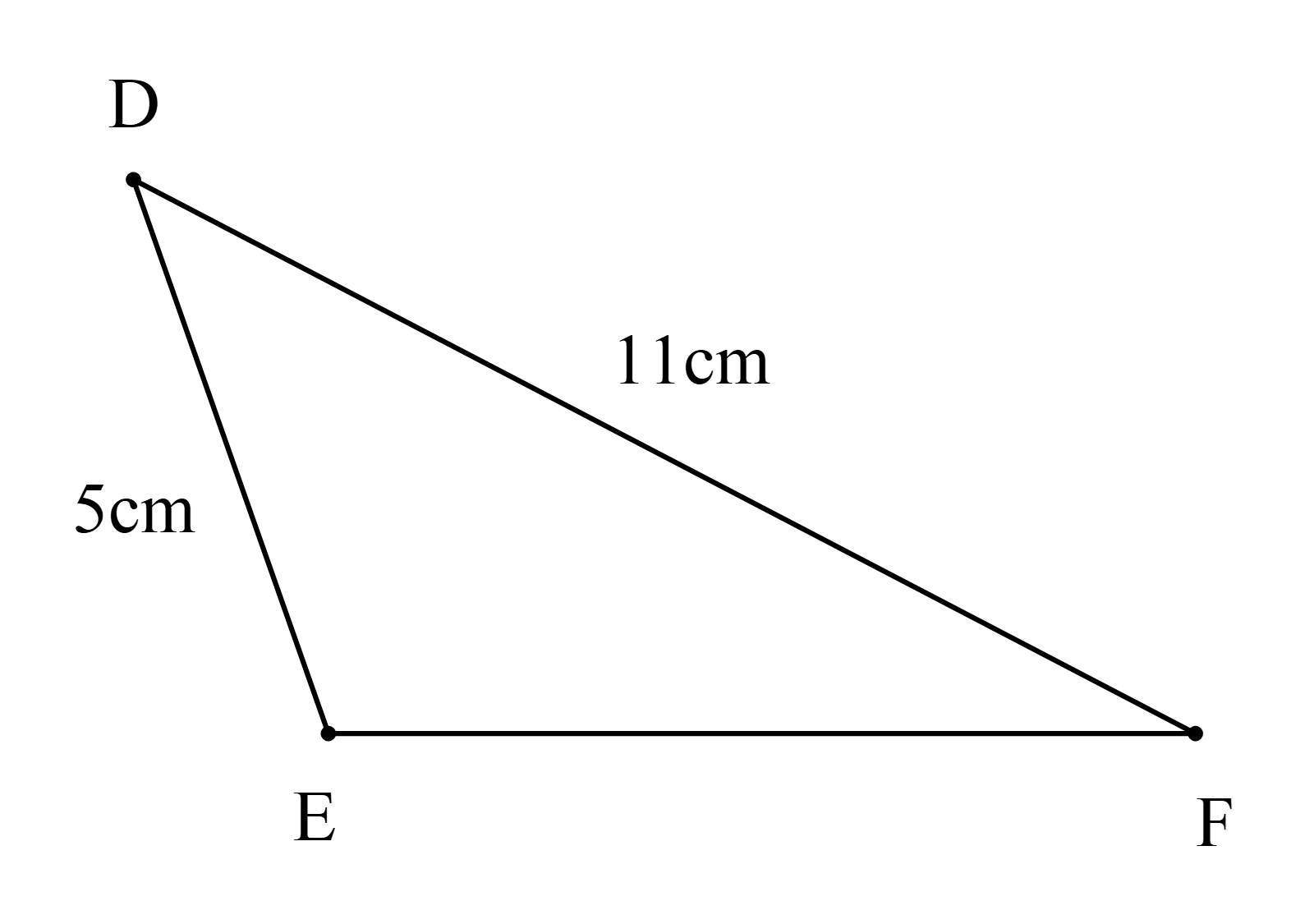
Độ dài cạnh EF là
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: D
Vì “Trong một tam giác, độ dài một cạnh bao giờ cũng lớn hơn hiệu và nhỏ hơn tổng độ dài của hai cạnh còn lại”
Áp dụng bất đẳng thức cho ∆DEF ta có:
DF – DE < EF < DF + DE
Do đó 11 – 5 < EF < 11 + 5
Hay 6 < EF < 16.
Trong 4 phương án ta thấy EF = 8 cm thỏa mãn điều kiện trên.
Vậy ta chọn phương án D.
Câu 10:
Cho hình vẽ
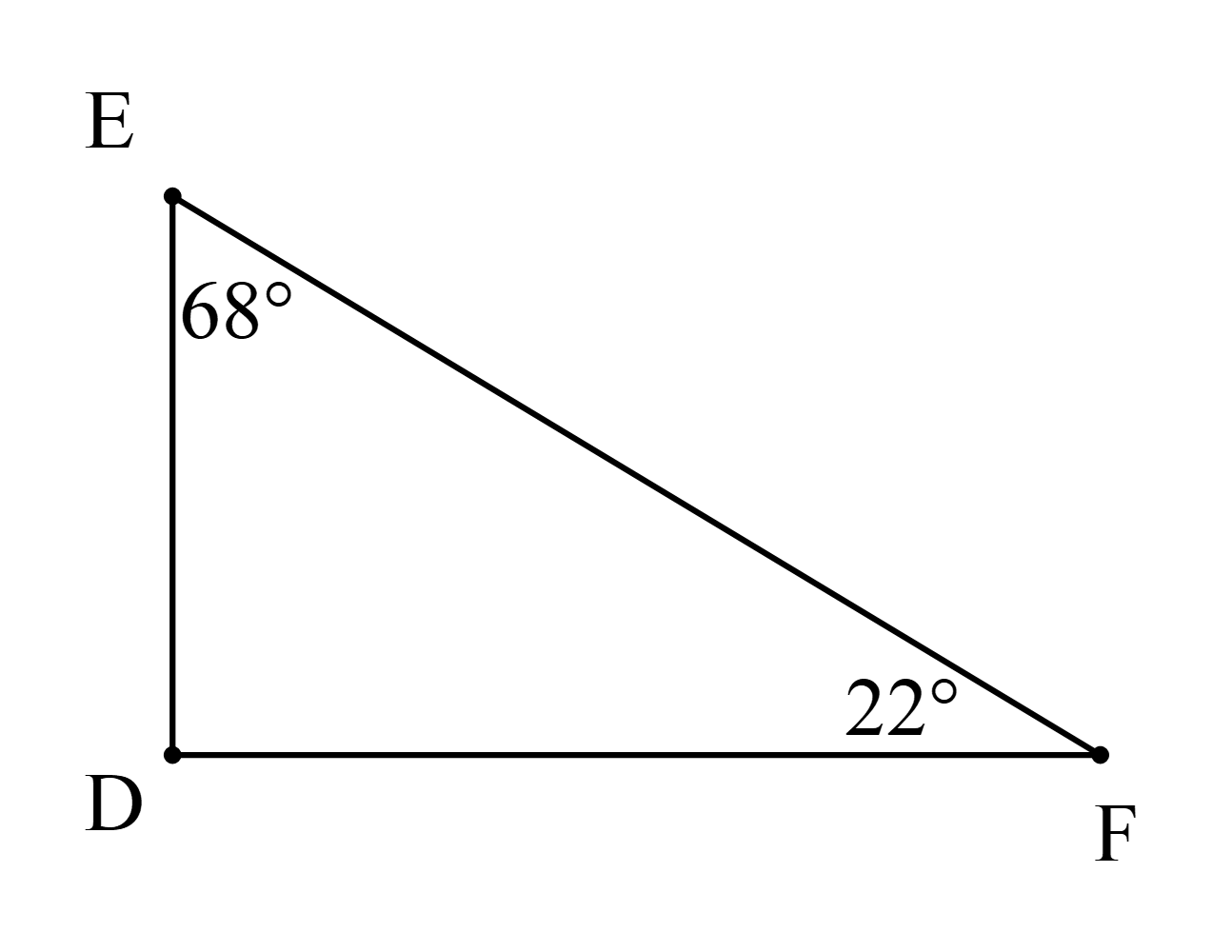
Chọn khẳng định đúng:
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: A
Xét ∆EDF có: \(\widehat {\rm{E}} + \widehat {\rm{D}} + \widehat {\rm{F}} = 180^\circ \) (tổng ba góc trong một tam giác bằng 180°)
Hay \(68^\circ + \widehat {\rm{D}} + 22^\circ = 180^\circ \).
Suy ra \(\widehat {\rm{D}} = 180^\circ - 68^\circ - 22^\circ = 90^\circ \).
Do đó ∆DEF là tam giác vuông tại D.
Vậy ta chọn phương án A.
Câu 11:
Cho AC = 2 cm; AB = 8 cm; BC = a cm (a ∈ ℕ). Có bao nhiêu giá trị của a để ABC là tam giác?
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: B
Theo bất đẳng thức tam giác ta có:
AB – AC < BC < AB + AC
Hay 8 – 2 < a < 8 + 2
Suy ra 6 < a < 10 (1)
Mà a ∈ ℕ (2)
Từ (1) và (2) suy ra a = 7 cm; a = 8 cm; a = 9 cm.
Do đó có tất cả 3 giá trị của a thỏa mãn để ABC là tam giác.
Vậy ta chọn phương án B
Câu 12:
Cho tam giác ABC có \(\widehat A = 70^\circ \) và \(\widehat B - \widehat C = 20^\circ .\) Tam giác ABC là tam giác gì?
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: A
Xét DABC có \(\widehat A + \widehat B + \widehat C = {180^o}\) (tổng ba góc trong một tam giác)
Hay \(70^\circ + \widehat B + \widehat C = {180^o}\)
Suy ra \(\widehat B + \widehat C = {180^o} - 70^\circ = 110^\circ \).
Mà \(\widehat B - \widehat C = 20^\circ .\)
Do đó \(\widehat B = \frac{{110^\circ + 20^\circ }}{2} = 65^\circ \) và \(\widehat C = {110^o} - \widehat B = 110^\circ - 65^\circ = 45^\circ .\)
Vì 45° < 65° < 70° < 90° nên ba góc A, B, C của tam giác ABC đều là góc nhọn.
Khi đó tam giác ABC là tam giác nhọn.
Vậy ta chọn phương án A.