Trắc nghiệm Toán 7 CTST Bài 7. Tính chất ba đường trung tuyến của tam giác có đáp án (Phần 2)
Trắc nghiệm Toán 7 CTST Bài 7. Tính chất ba đường trung tuyến của tam giác có đáp án (Phần 2) (Thông hiểu)
-
687 lượt thi
-
7 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 1:
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: B
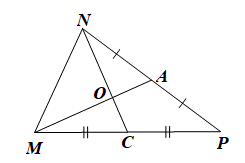
Xét DMNP có O là giao điểm của hai đường trung tuyến MA, NC nên O là trọng tâm tam giác MNP.
Suy ra NO = \(\frac{2}{3}\)NC, MO = \(\frac{2}{3}\)MA
Do đó OC = \(\frac{1}{3}\)NC hay NC = 3OC và MA = \(\frac{3}{2}\)MO.
Mà MO = 2,5 cm, OC = 1 cm (giả thiết)
Nên NC = 3 . 1 = 3 (cm), MA = \(\frac{3}{2}\). 2,5 = 3,75 (cm).
Vậy ta chọn phương án B.
Câu 2:
Cho tam giác ABC có trung tuyến AM và BN là hai đường trung tuyến, AM = BN. Tam giác ABC là tam giác gì?
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: B
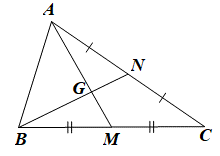
Gọi G là giao điểm của AM và BN.
Xét DABC có hai đường trung tuyến AM và BN cắt nhau tại G nên G là trọng tâm tam giác ABC.
Suy ra \({\rm{AG = }}\frac{2}{3}{\rm{AM}}\), \({\rm{BG = }}\frac{2}{3}{\rm{BN}}\)
Do đó \({\rm{MG = }}\frac{1}{3}{\rm{AM}}\), \({\rm{NG = }}\frac{1}{3}{\rm{BN}}\).
Mà AM = BN (giả thiết) nên AG = BG, MG = NG.
Xét ΔAGN và ΔBGM có
AG = BG (chứng minh trên),
\(\widehat {AGN} = \widehat {BGM}\) (hai góc đối đỉnh),
NG = MG (chứng minh trên)
Do đó ΔAGN = ΔBGM (c.g.c)
Suy ra AN = BM (hai cạnh tương ứng)
Lại có AN = \(\frac{1}{2}\)AC (vì N là trung điểm của AC);
BM = \(\frac{1}{2}\)BC (vì M là trung điểm của BC).
Nên AC = BC.
Suy ra tam giác ABC cân tại C.
Vậy ta chọn phương án B.
Câu 3:
Cho tam giác ABC. Tên tia đối của BA lấy D sao cho BD = BA. Trên cạnh BC lấy E sao cho CE = 2BE. Gọi K là giao điểm của AE và CD. Chọn khẳng định đúng?
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: A
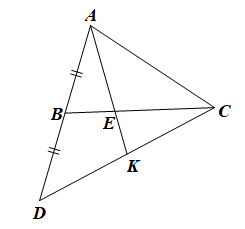
Ta có CE = 2BE nên BE = \(\frac{1}{2}CE\)
Do đó BC = CE + BE = CE + \(\frac{1}{2}\)CE = \(\frac{3}{2}\)CE
Suy ra CE = \(\frac{2}{3}\)BC.
Xét DACD có CB là đường trung tuyến (do AB = BD) và E nằm trên BC thỏa mãn CE = \(\frac{2}{3}\)BC.
Suy ra E là trọng tâm tam giác ACD.
Mà K là giao điểm của AE và CD (giả thiết).
Nên AK là đường trung tuyến trong tam giác ACD.
Suy ra K là trung điểm của CD.
Hay DK = KC = \(\frac{1}{2}\)CD.
Vậy ta chọn phương án A.
Câu 4:
Cho tam giác MNP cân tại M. Hai đường trung tuyến NE, PF cắt nhau tại I. Kéo dài MI cắt NP tại H. Chọn phát biểu sai trong các phát biểu sau:
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: C
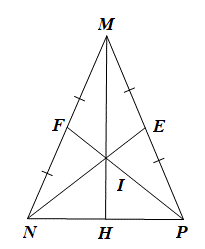
Xét DMNP có hai đường trung tuyến NE và PF cắt nhau tại I nên I là trọng tâm tam giác MNP.
Suy ra MH là đường trung tuyến của tam giác MNP.
Do đó H là trung điểm của NP hay NH = PH.
Vì tam giác MNP cân tại M nên MN = MP
Xét DMNH và DMPH có:
NH = PH (chứng minh trên),
MH là cạnh chung,
MN = MP (chứng minh trên)
Do đó DMNH = DMPH (c.c.c)
Suy ra \(\widehat {MHN} = \widehat {MHP}\) (hai góc tương ứng)
Mà \(\widehat {MHN} + \widehat {MHP} = 180^\circ \)(hai góc kề bù)
Do đó \(\widehat {MHN} = \widehat {MHP} = \frac{{180^\circ }}{2} = 90^\circ \)
Hay MH vuông góc NP tại trung điểm H của NP.
Suy ra MH là trung trực của NP.
Vậy ta chọn phương án C.
Câu 5:
Cho tam giác ABC nhọn. Các đường trung tuyến AM, BN cắt nhau tại G. Trên tia đối của NB lấy điểm I sao cho NI = BN. Chọn đáp án đúng?
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: C
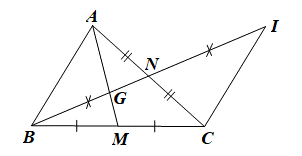
Vì BN là trung tuyến nên N là trung điểm của AC.
Suy ra AN = CN
Xét DABN và DICN có
AN = NC (chứng minh trên),
\(\widehat {ANB} = \widehat {CNI}\) (hai góc đối đỉnh),
NB = NI (giả thiết)
Do đó DABN = DCIN (c.g.c)
Vậy ta chọn phướng án C.
Câu 6:
Cho tam giác DEF có DM, EN là hai đường trung tuyến cắt nhau tại G. Kéo dài DM lấy điểm H sao cho MH = MD. Kéo dài EN lấy điểm K sao cho NK = NE. Chọn khẳng định sai?
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
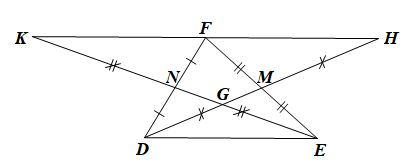
• Xét DKFN và DEDN có
NF = ND (vì N là trung điểm của DF),
\(\widehat {KNF} = \widehat {END}\) (hai góc đối đỉnh),
KN = EN (giả thiết)
Do đó DKFN = DEDN (c.g.c)
Suy ra KF = DE (hai cạnh tương ứng).
Do đó phương án A là đúng.
• Chứng minh tương tự ta cũng có: DFHM = DEDM (c.g.c)
Suy ra HF = DE (hai cạnh tương ứng).
Do đó phương án B là đúng.
• Do DFHM = DEDM (c.g.c) nên \(\widehat {MHF} = \widehat {MDE}\)(hai góc tương ứng)
Mà hai góc này ở vị trí so le trong
Suy ra FH // DE. Do đó phương án D là đúng.
Vậy ta chọn phương án C.
Câu 7:
Cho tam giác MNP cân tại P. Hai đường trung tuyến MH và NK cắt nhau tại G. Kéo dài PG cắt MN tại I. Gọi E, F lần lượt là trung điểm của GP và GM. Trong các khẳng định sau có bao nhiêu khẳng định đúng?
(I) Các đường thẳng PF, GK, ME cắt nhau tại một điểm;
(II) DPIN = DPIM;
(III) G là trọng tâm tam giác MNP;
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: D
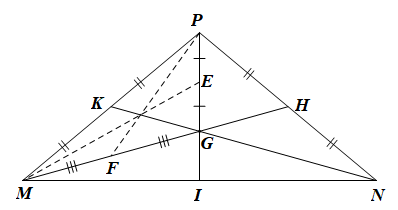
Xét DMNP có hai đường trung tuyến MH và NK cắt nhau tại G nên G là trọng tâm tam giác MNP. Do đó khẳng định (III) là đúng.
G là trọng tâm tam giác MNP nên PI là đường trung tuyến của tam giác.
Suy ra I là trung điểm của MN hay MI = NI.
Xét DPIN và DPIM có
NI = MI (chứng minh trên),
PI là cạnh chung,
PN = PM (do DMNP cân tại P)
Do đó DPIN = DPIM (c.c.c) nên khẳng định (II) là đúng.
Xét DPGM có PF, GK, ME là các đường trung tuyến của tam giác nên ba đường này cắt nhau tại một điểm. Do đó khẳng định (I) là đúng.
Vậy cả 3 khẳng định đều đúng, ta chọn phương án D.
