Trắc nghiệm Toán 7 CTST Bài tập cuối chương 8 có đáp án (Phần 2) (Vận dụng)
-
652 lượt thi
-
7 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 1:
Ba vị trí của khu vực A, B, C trong một trường học được mô tả như hình vẽ dưới đây.
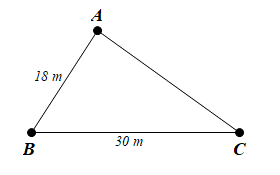
Nếu đặt ở khu vực A một thiết bị phát wifi thì cần có bán kính hoạt động là bao nhiêu để cả hai khu vực B và C đều nhận được tín hiệu?
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: D
Theo bất đẳng thức ta có:
BC – AB < AC < BC + AC
Hay 30 – 18 < AC < 30 + 18
Suy ra 12 < AC < 48
Nếu đặt ở khu vực A một thiết bị phát wifi đảm bảo cả hai khu vực B và C đều nhận được tín hiệu thì bán kính hoạt động cần lớn hơn khoảng cách AB và AC.
Do đó trong các bán kính hoạt động của thiết bị phát wifi được nêu ở các phương án thì bán kính hợp lí là 48 m.
Ta chọn phương án D.
Câu 2:
Một con đường quốc lộ có vị trí với hai điểm dân cư A và B như hình vẽ dưới đây.
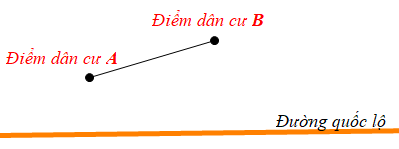
Hãy tìm trên đường quốc lộ đó một địa điểm C để xây dựng trạm y tế sao cho trạm y tế cách đều hai điểm dân cư A và B.
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: C
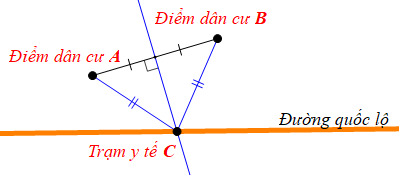
Vì trạm y tế C cách đều hai khu dân cư A và B.
Nên C thuộc đường trung trực d của đoạn thẳng AB nối hai khu dân cư.
Mà C nằm trên đường quốc lộ nên C là giao điểm của đường quốc lộ và đường trung trực của đoạn thẳng nối hai khu dân cư.
Do đó để xây dựng trạm y tế ở bên đường cách đều hai điểm dân cư thì trạm y tế đó phải là giao điểm giữa con đường quốc lộ và đường trung trực của đoạn thẳng AB nối hai khu dân cư.
Vậy ta chọn phương án C.
Câu 3:
Hai nhà máy được xây dựng tại hai địa điểm A và B cùng nằm về một phía của khúc sông thẳng. Lấy điểm mốc D ở phía bên kia bờ sông là điểm đối xứng của nhà máy A qua khúc sông thẳng.
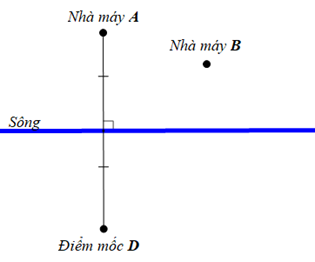
Tìm trên bờ sông một địa điểm C để xây dựng trạm bơm sao cho tổng chiều dài đường ống dẫn nước từ C đến A và đến B nhỏ nhất.
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: A
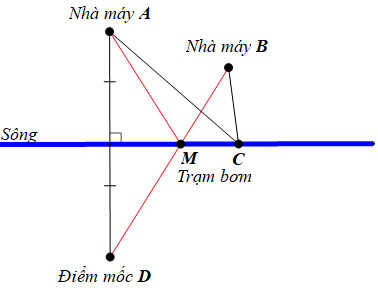
Vì D là điểm đối xứng của A qua bờ sông
Nên bờ sông chính là đường trung trực của AD.
Do đó CA = CD (tính chất đường trung trực)
Suy ra CA + CB = CD + CB.
Gọi M là giao điểm của BD và bờ sông.
+) Nếu C không trùng với M, ta xét ∆BCD, có:
CB + CD > BD hay CA + CB > BD (1).
+) Nếu C trùng với M thì:
CA + CB = CD + CB = MD + MB = BD (2).
Từ (1), (2), ta suy ra CA + CB ≥ BD.
Do đó khi C trùng với M hay C là giao điểm của BD với bờ sông thì giá trị của tổng CA + CB là nhỏ nhất.
Vậy ta chọn phương án A.
Câu 4:
Cho tam giác ABC có \(\widehat A = \alpha \) là góc tù. Các đường trung trực của các cạnh AB và AC cắt nhau tại I. Tính số đo của góc BIC theo α ta được:
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: C
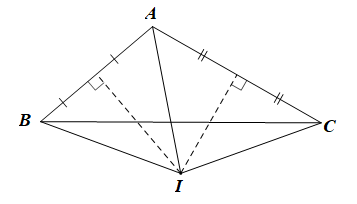
Xét DABC có I là giao điểm của hai đường trung trực của AB và AC nên I cách đều ba đỉnh của tam giác.
Do đó IA = IB = IC.
• Tam giác IAB có IA = IB nên cân tại I
Suy ra \[\widehat {IAB} = \widehat {IBA}\] (tính chất tam giác cân).
• Tam giác IAC có IA = IC nên cân tại I
Suy ra \[\widehat {IAC} = \widehat {ICA}\] (tính chất tam giác cân).
Xét DABI có \[\widehat {IAB} + \widehat {IBA} + \widehat {AIB} = 180^\circ \] (tổng ba góc trong một tam giác)
Mà \[\widehat {IAB} = \widehat {IBA}\](chứng minh trên)
Suy ra \[\widehat {AIB} = 180^\circ - 2.\widehat {IAB}\]
Xét DACI có \[\widehat {IAC} + \widehat {ICA} + \widehat {AIC} = 180^\circ \] (tổng ba góc trong một tam giác)
Mà \[\widehat {IAC} = \widehat {ICA}\] (chứng minh trên)
Suy ra \[\widehat {AIC} = 180^\circ - 2.\widehat {IAC}\]
Ta có \(\widehat {BIC} = \widehat {AIB} + \widehat {AIC} = 180^\circ - 2.\widehat {IAB} + 180^\circ - 2.\widehat {IAC}\)
Hay \(\widehat {BIC} = 360^\circ - 2.(\widehat {IAB} + .\widehat {IAC}) = 360^\circ - 2.\widehat {BAC} = 360^\circ - 2\alpha \).
Vậy ta chọn phương án C.
Câu 5:
Cho ∆ABC có AD, BE, CF là ba đường trung tuyến và trọng tâm G.
Cho các phát biểu sau:
(I) \[AD + BE + CF > \frac{3}{4}\left( {AB + BC + AC} \right)\];
(II) AD + BE + CF < AB + BC + AC.
Chọn khẳng định đúng:
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: C
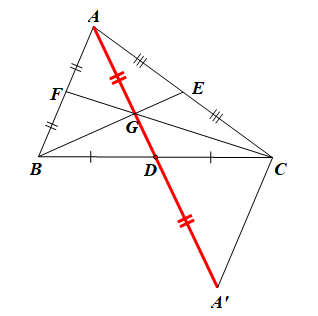
• Ta xét (I):
Vì G là trọng tâm của ∆ABC nên ta có \(GB = \frac{2}{3}BE\) và \(GC = \frac{2}{3}CF\).
∆GBC có GB + GC > BC (bất đẳng thức tam giác).
Suy ra \(\frac{2}{3}BE + \frac{2}{3}CF > BC\).
Hay \(\frac{2}{3}\left( {BE + CF} \right) > BC\).
Do đó \(BE + CF > \frac{3}{2}BC\) (1).
Chứng minh tương tự ta được:
+) \(AD + BE > \frac{3}{2}AB\) (2).
+) \(AD + CF > \frac{3}{2}AC\) (3).
Lấy (1) + (2) + (3) vế theo vế, ta được:
\(2AD + 2BE + 2CF > \frac{3}{2}AB + \frac{3}{2}BC + \frac{3}{2}AC\).
Suy ra \(2\left( {AD + BE + CF} \right) > \frac{3}{2}\left( {AB + BC + AC} \right)\).
Do đó \(AD + BE + CF > \frac{3}{4}\left( {AB + BC + AC} \right)\).
Vậy (I) đúng.
• Ta xét (II):
Trên tia AD, lấy điểm A’ sao cho DA’ = DA.
Xét ∆ADB và ∆A’DC, có:
DA = DA’,
\(\widehat {ADB} = \widehat {A'DC}\) (hai góc đối đỉnh),
BD = CD (do AD là đường trung tuyến của ∆ABC),
Do đó ∆ADB = ∆A’DC (c.g.c).
Suy ra AB = A’C (hai cạnh tương ứng).
Áp dụng bất đẳng thức tam giác cho ∆AA’C, ta được:
AA’ < AC + A’C.
Suy ra AA’ < AC + AB hay 2AD < AC + AB (4).
Chứng minh tương tự, ta được:
+) 2BE < AB + BC (5).
+) 2CF < AC + BC (6).
Lấy (4) + (5) + (6) vế theo vế, ta được:
2AD + 2BE + 2CF < 2AC + 2AB + 2BC.
Suy ra 2(AD + BE + CF) < 2(AB + AC + BC).
Do đó AD + BE + CF < AB + AC + BC.
Vậy (II) đúng.
Kết luận: cả (I) và (II) đều đúng.
Ta chọn phương án C.
Câu 6:
Cho tam giác MNP có ba đường phân giác MA, NB, PC cắt nhau tại I. Vẽ IH vuông góc NP tại H. Khẳng định nào dưới đây là đúng:
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: C
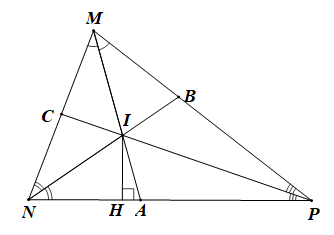
Xét DMNP có ba đường phân giác MA, NB, PC cắt nhau tại I nên I cách đều ba cạnh của tam giác.
Điểm I không phải là giao điểm ba đường trung trực của tam giác nên không cách đều ba đỉnh. Do đó phương án B, D là sai.
Vì MI là tia phân giác của góc NMP nên \(\widehat {NMI} = \widehat {PMI} = \frac{1}{2}\widehat {PMN}\).
Vì NI là tia phân giác của góc MNP nên \(\widehat {MNI} = \widehat {PNI} = \frac{1}{2}\widehat {MNP}\).
Vì PI là đường phân giác của góc MPN nên \(\widehat {NPI} = \widehat {MPI} = \frac{1}{2}\widehat {MPN}\).
Xét DMIP có \(\widehat {MIP} + \widehat {MPI} + \widehat {PMI} = 180^\circ \) (tổng ba góc trong một tam giác)
Nên \(\widehat {MIP} = 180^\circ - \left( {\widehat {MPI} + \widehat {PMI}} \right)\)
Suy ra \(\widehat {MIP} = 180^\circ - \frac{1}{2}\left( {\widehat {MPN} + \widehat {PMN}} \right)\).
Xét DMNP có \(\widehat {MNP} + \widehat {MPN} + \widehat {PMN} = 180^\circ \)(tổng ba góc trong một tam giác)
Nên \(\widehat {MPN} + \widehat {PMN} = 180^\circ - \widehat {MNP}\).
Do đó \(\widehat {MIP} = 180^\circ - \frac{1}{2}\left( {180^\circ - \widehat {MNP}} \right)\)
Hay \(\widehat {MIP} = 180^\circ - 90^\circ + \frac{1}{2}\widehat {MNP} = 90^\circ + \frac{1}{2}\widehat {MNP}\).
Ta có \(\widehat {MIP} + \widehat {PIA} = 180^\circ \) (hai góc kề bù)
Nên \(\widehat {PIA} = 180^\circ - \widehat {MIP} = 180^\circ - \left( {90^\circ + \frac{1}{2}\widehat {MNP}} \right) = 90^\circ - \frac{1}{2}\widehat {MNP}\) (1)
Vì DINH vuông tại H nên \(\widehat {HIN} + \widehat {HNI} = 90^\circ \) (trong tam giác vuông, tổng hai góc nhọn bằng 90°)
Suy ra \(\widehat {HIN} = 90^\circ - \widehat {HNI} = 90^\circ - \frac{1}{2}\widehat {MNP}\) (2)
Từ (1) và (2) suy ra \(\widehat {NIH} = \widehat {PIA}\).
Vậy ta chọn phương án C.
Câu 7:
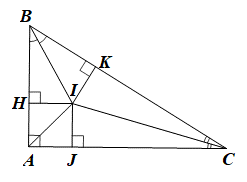
Cho tam giác ABC vuông tại A. Các tia phân giác của các góc B và C cắt nhau tại I. Gọi H, J, K lần lượt là chân đường vuông góc kẻ từ I đến AB, AC, BC. Biết KI = 5 cm, BK = 10 cm, KC = 15 cm. Diện tích tam giác ABC bằng:
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đáp án đúng là:
Xét DBHI và DBKI có:
\(\widehat {BHI} = \widehat {BKI} = 90^\circ \),
BI là cạnh chung;
\(\widehat {HBI} = \widehat {KBI}\) (do BI là tia phân giác của góc ABC),
Do đó DBHI = DBKI (cạnh huyền – góc nhọn).
Suy ra BH = BK = 10 cm (hai cạnh tương ứng).
Chứng minh tương tự có DIJC = DIKC (cạnh huyền – góc nhọn).
Suy ra JC = KC = 15 cm.
Vì các tia phân giác của các góc B và C cắt nhau tại I nên I là giao điểm của ba đường phân giác của tam giác ABC.
Do đó AI là tia phân giác của góc A nên \(\widehat {HAI} = \widehat {JAI} = \frac{1}{2}.90^\circ = 45^\circ .\)
Tam giác AHI vuông tại H có \(\widehat {HAI} = 45^\circ \) nên là tam giác vuông cân tại H.
Do đó IH = AH.
Chứng minh tương tự ta cũng có tam giác AJI vuông cân tại J nên AJ = IJ.
Mà I là giao điểm của ba đường phân giác của tam giác ABC nên I cách đều ba cạnh của tam giác, hay IH = IK = IJ = 5 cm.
Suy ra AH = AJ = IH = IK = IJ = 5 cm.
Ta có AB = AH + BH = 5 + 10 = 15 (cm);
AC = AJ + JC = 5 + 15 = 20 (cm).
Diện tích tam giác ABC là:
\(\frac{1}{2}\).15.20 = 150 (cm2).
Vậy ta chọn phương án C.
