Trắc nghiệm Toán 7 KNTT Bài 15: Các trường hợp bằng nhau của tam giác vuông có đáp án
Dạng 2: Sử dụng trường hợp bằng nhau của hai tam giác vuông để chứng minh tính chất khác có đáp án
-
1155 lượt thi
-
10 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 1:
Cho ∆ABC vuông tại A và ∆MNP vuông tại M có AB = MN, CB = PN. Biết AC = 5 cm. Tính độ dài MP.
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
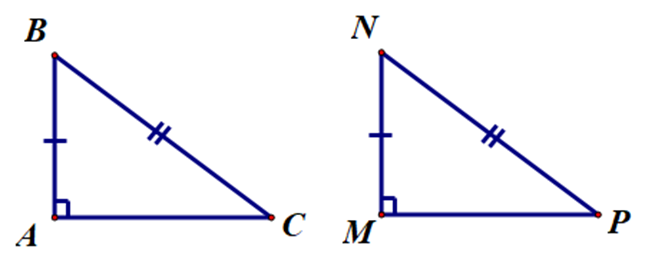
Xét ∆ABC và ∆MNP, có:
\[\widehat {BAC} = \widehat {NMP} = 90^\circ \].
AB = MN (giả thiết).
CB = PN (giả thiết).
Do đó ∆ABC = ∆MNP (cạnh huyền – cạnh góc vuông).
Ta suy ra AC = MP (hai cạnh tương ứng).
Khi đó ta có MP = AC = 5 cm.
Vậy ta chọn đáp án B.
Câu 2:
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
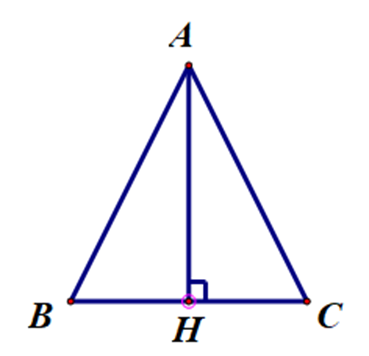
Ta xét từng đáp án:
Đáp án A:
Xét ∆AHB và ∆AHC, có:
\[\widehat {AHB} = \widehat {AHC} = 90^\circ \].
AH là cạnh chung.
AB = AC (giả thiết).
Do đó ∆AHB = ∆AHC (cạnh huyền – cạnh góc vuông).
Ta suy ra đáp án A sai.
Đến đây ta có thể chọn đáp án A.
Đáp án B:
Ta có ∆AHB = ∆AHC (chứng minh trên).
Ta suy ra \[\widehat {BAH} = \widehat {CAH}\] (cặp góc tương ứng).
Do đó AH là phân giác \[\widehat {BAC}\].
Vậy đáp án B đúng.
Đáp án C:
Ta có ∆AHB = ∆AHC (chứng minh trên).
Ta suy ra BH = CH (cặp cạnh tương ứng).
Do đó đáp án C đúng.
Đáp án D:
Ta có ∆AHB = ∆AHC (chứng minh trên).
Ta suy ra \[\widehat {ABH} = \widehat {ACH}\] (cặp góc tương ứng).
Do đó đáp án D đúng.
Vậy ta chọn đáp án A.
Câu 3:
Cho ∆ABC có AI, BH, CK là các đường cao (I ∈ BC, K ∈ AB, H ∈ AC). Biết ∆ABH = ∆ACK. Kết luận nào sau đây đúng?
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
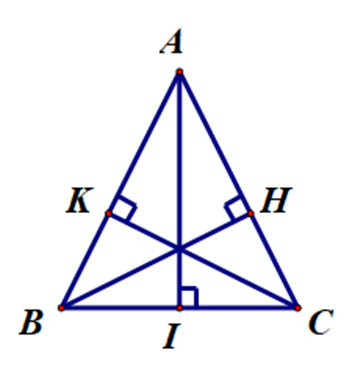
Ta có ∆ABH = ∆ACK (giả thiết).
Ta suy ra \[\widehat {HBA} = \widehat {KCA}\]; HB = KC (cặp góc, cặp cạnh tương ứng).
Do đó đáp án A, B sai.
Ta có: ∆ABH = ∆ACK (giả thiết).
Mà \[\widehat {ABH},\,\,\widehat {KAC}\] không phải cặp góc tương ứng.
Do đó \[\widehat {ABH} \ne \widehat {KAC}\].
Suy ra đáp án C sai.
Ta có: ∆ABH = ∆ACK (giả thiết).
Ta suy ra AH = AK và AB = AC (các cặp góc tương ứng).
Do đó AB – AK = AC – AH.
Suy ra BK = CH (vì K ∈ AB, H ∈ AC).
Do đó đáp án D đúng.
Vậy ta chọn đáp án D.
Câu 4:
Cho ∆ABC vuông tại A. Trên cạnh BC, lấy điểm D sao cho BD = BA = 5 cm. Đường thẳng vuông góc với BC tại D cắt AC tại H. Gọi E là giao điểm của DH và AB. Biết CD = 3 cm. Độ dài cạnh BE bằng
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
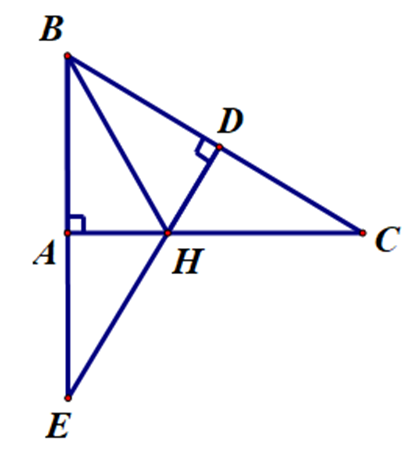
Xét ∆BAH và ∆BDH, có:
\[\widehat {BAH} = \widehat {BDH} = 90^\circ \].
BH là cạnh chung.
BA = BD (giả thiết).
Do đó ∆BAH = ∆BDH (cạnh huyền – cạnh góc vuông).
Ta suy ra AH = DH (cặp cạnh tương ứng).
Xét ∆AHE và ∆DHC, có:
\[\widehat {HAE} = \widehat {HDC} = 90^\circ \].
AH = DH (chứng minh trên).
\[\widehat {AHE} = \widehat {DHC}\] (2 góc đối đỉnh).
Do đó ∆AHE = ∆DHC (cạnh góc vuông – góc nhọn kề).
Ta suy ra AE = DC.
Ta có BA = BD (giả thiết) và AE = DC (chứng minh trên).
Suy ra BA + AE = BD + DC.
Do đó BE = BD + DC = 5 + 3 = 8 (cm).
Vậy ta chọn đáp án C.
Câu 5:
Tìm x trong hình bên.
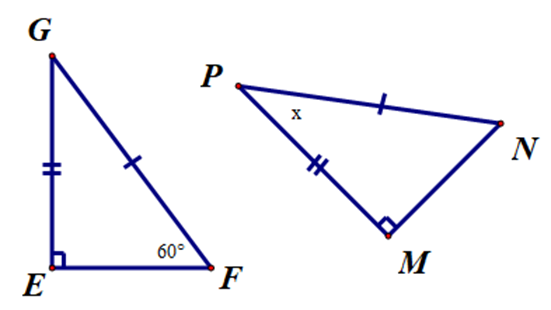
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
Xét ∆EFG và ∆MNP, có:
\[\widehat {{\rm{GEF}}} = \widehat {PMN} = 90^\circ \].
GE = PM (giả thiết).
GF = PN (giả thiết).
Do đó ∆EFG = ∆MNP (cạnh huyền – cạnh góc vuông).
Ta suy ra \[\widehat {{\rm{EGF}}} = \widehat {MPN}\] (cặp góc tương ứng).
Hay \[\widehat {{\rm{EGF}}} = x\].
∆EFG vuông tại E: \[\widehat {{\rm{EGF}}} + \widehat {EFG} = 90^\circ \] (trong tam giác vuông, hai góc nhọn phụ nhau)
Suy ra \[\widehat {EGF} = 90^\circ - \widehat {EFG} = 90^\circ - 60^\circ = 30^\circ \].
Do đó x = 30°.
Vậy ta chọn đáp án A.
Câu 6:
Cho ∆ABC nhọn và ∆ABC = ∆DEF. Kẻ AH ⊥ BC (H ∈ BC) và DK ⊥ EF (K ∈ EF). Kết luận nào sau đây là đúng?
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
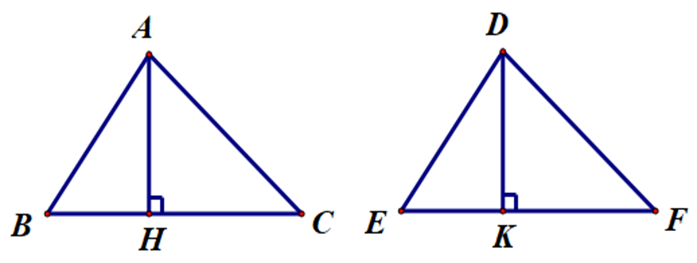
Xét ∆ABH và ∆DEK, có:
\[\widehat {AHB} = \widehat {DKE} = 90^\circ \].
AB = DE (vì ∆ABC = ∆DEF).
\[\widehat {ABH} = \widehat {DEK}\] (vì ∆ABC = ∆DEF).
Do đó ∆ABH = ∆DEK (cạnh huyền – góc nhọn).
Ta suy ra AH = DK; BH = EK và \[\widehat {BAH} = \widehat {EDK}\] (các cặp cạnh và cặp góc tương ứng).
Do đó cả A, B, C đều đúng.
Vậy ta chọn đáp án D.
Câu 7:
Cho ∆ABC vuông tại A, tia phân giác \[\widehat B\] cắt AC tại D. Kẻ DE ⊥ BC tại E. Gọi H là giao điểm của BD và AE. Đường thẳng BH vuông góc với đường thẳng nào trong các đường thẳng sau đây.
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
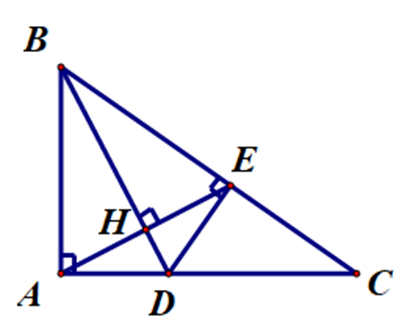
Xét ∆ABD và ∆EBD, có:
\[\widehat {BAD} = \widehat {BED} = 90^\circ \].
BD là cạnh chung.
\[\widehat {ABD} = \widehat {EBD}\] (BD là phân giác của \[\widehat {BAC}\]).
Do đó ∆ABD = ∆EBD (cạnh huyền – góc nhọn).
Suy ra AB = BE (cặp cạnh tương ứng).
Xét ∆ABH và ∆EBH, có:
AB = BE (chứng minh trên).
BH là cạnh chung.
\[\widehat {ABH} = \widehat {EBH}\] (BD là phân giác của \[\widehat {BAC}\]).
Do đó ∆ABH = ∆EBH (cạnh – góc – cạnh).
Suy ra \[\widehat {AHB} = \widehat {BHE}\] (hai góc tương ứng)
Mà \[\widehat {AHB} + \widehat {BHE} = 180^\circ \] (hai góc kề bù).
Suy ra \[\widehat {AHB} = \widehat {BHE} = \frac{{180^\circ }}{2} = 90^\circ \].
Do đó BH ⊥ AE.
Vậy ta chọn đáp án B.
Câu 8:
Cho hình vẽ:
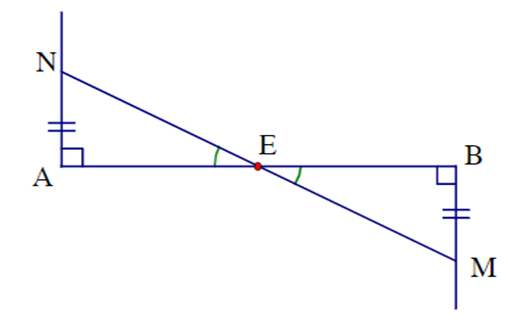
Kết luận nào sau đây sai?
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
Vì trong tam giác vuông, hai góc nhọn phụ nhau nên ta có:
∆AEN vuông tại A: \[\widehat {AEN} + \widehat {ANE} = 90^\circ \] (1).
∆BEM vuông tại B: \[\widehat {BEM} + \widehat {BME} = 90^\circ \] (2).
Ta có \[\widehat {AEN} = \widehat {BEM}\] (2 góc đối đỉnh) (3).
Từ (1), (2), (3), ta suy ra \[\widehat {ANE} = \widehat {BME}\].
Do đó đáp án C đúng.
Xét ∆AEN và ∆BEM, có:
\[\widehat {NAE} = \widehat {MBE} = 90^\circ \].
AN = BM (giả thiết).
\[\widehat {ANE} = \widehat {BME}\] (chứng minh trên).
Do đó ∆AEN = ∆BEM (cạnh góc vuông – góc nhọn kề).
Ta có ∆AEN = ∆BEM (chứng minh trên).
Suy ra EN = EM (hai cạnh tương ứng).
Khi đó E là trung điểm MN.
Do đó đáp án A đúng.
Ta có ∆AEN = ∆BEM (chứng minh trên).
Suy ra AE = BE (hai cạnh tương ứng).
Khi đó E là trung điểm AB.
Do đó đáp án B đúng.
Đáp án D sai vì AE, ME không phải là cặp cạnh tương ứng trong hai tam giác bằng nhau ∆AEN và ∆BEM.
Vậy ta chọn đáp án D.
Câu 9:
Cho ∆ABC có M là trung điểm BC. Kẻ BE và CF lần lượt cùng vuông góc với AM ở E và F. Khi đó ta có BF song song với đường thẳng nào trong các đường thẳng sau đây.
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
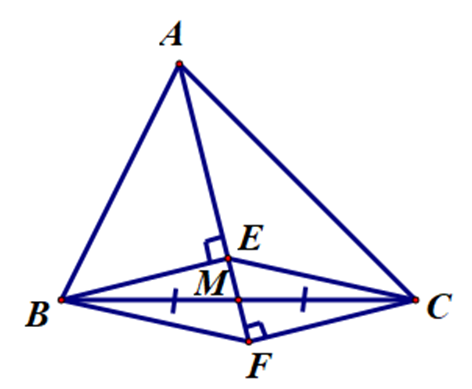
Xét ∆BME và ∆CMF, có:
BM = CM (M là trung điểm BC).
\[\widehat {BEM} = \widehat {CFM} = 90^\circ \].
\[\widehat {BME} = \widehat {CMF}\] (hai góc đối đỉnh).
Do đó ∆BME = ∆CMF (cạnh huyền – góc nhọn).
Ta suy ra ME = MF (cặp cạnh tương ứng).
Xét ∆BMF và ∆CME, có:
MF = ME (chứng minh trên).
BM = CM (M là trung điểm BC).
\[\widehat {BMF} = \widehat {CME}\] (hai góc đối đỉnh).
Do đó ∆BMF = ∆CME (cạnh – góc – cạnh).
Ta suy ra \[\widehat {MBF} = \widehat {MCE}\].
Mà hai góc này ở vị trí so le trong.
Do đó ta có BF // CE.
Vậy ta chọn đáp án A.
Câu 10:
Cho ∆ABC vuông tại A có AB < AC, \[\widehat B = 60^\circ \]. Kẻ AH ⊥ BC (H ∈ BC). Gọi D là điểm trên cạnh AC sao cho AD = AB. Kẻ DE ⊥ BC (E ∈ BC) và DK ⊥ AH (K ∈ AH). Cho các khẳng định sau:
(I) BH = AK;
(II) HA = KD = HE.
Chọn phương án đúng:
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
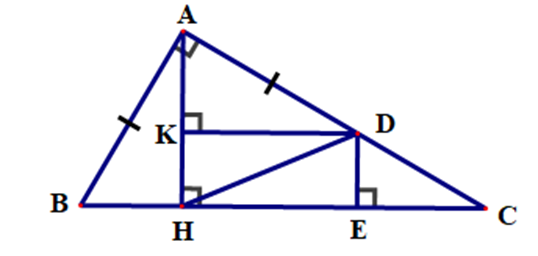
Xét ∆HAB và ∆KDA, có:
\[\widehat {AHB} = \widehat {DKA} = 90^\circ \].
AB = AD (giả thiết).
\[\widehat {BAH} = \widehat {ADK}\] (cùng phụ với \[\widehat {KAD}\]).
Do đó ∆HAB = ∆KDA (cạnh huyền – góc nhọn).
Suy ra HA = KD và BH = AK (các cặp cạnh tương ứng).
Do đó (I) đúng.
Ta có: KD ⊥ AH (giả thiết) và HE ⊥ AH (giả thiết).
Suy ra KD // HE.
Có \[\widehat {KDH},\,\,\widehat {EHD}\] ở vị trí so le trong.
Do đó \[\widehat {KDH} = \widehat {EHD}\].
Xét ∆KDH và ∆EHD, có:
\[\widehat {DKH} = \widehat {HED} = 90^\circ \].
HD là cạnh chung.
\[\widehat {KDH} = \widehat {EHD}\] (chứng minh trên).
Do đó ∆KDH = ∆EHD (cạnh huyền – góc nhọn).
Suy ra KD = EH (hai cạnh tương ứng)
Mà HA = KD (chứng minh trên).
Do đó HA = KD = HE. Suy ra (II) đúng.
Vậy ta chọn đáp án C.
