15 câu hỏi trắc nghiệm thuộc Trắc nghiệm Toán 7 KNTT Bài ôn tập cuối chương 4 (Thông hiểu) có đáp án

Câu 1:

Cho ∆ABC có AB = AC. Gọi D, E là hai điểm thuộc cạnh BC sao cho BD = DE = EC. Biết AD = AE. Khẳng định nào sau đây đúng nhất?

A. BE = CD;

B. ∆ABE = ∆ACD;

C. $\hat{E A B} = \hat{D A C}$ ;

D. Cả A, B, C đều đúng.

Xem đáp án

Hướng dẫn giải

Đáp án đúng là: D

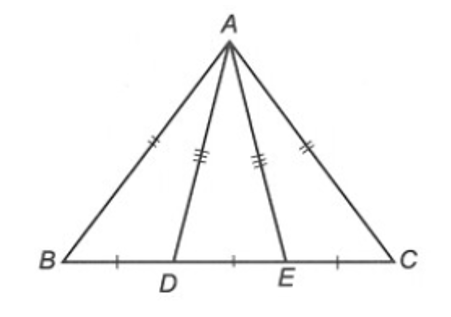
Cho tam giác ABC có AB = AC. Gọi D, E là hai điểm thuộc cạnh BC sao cho BD = DE = EC (ảnh 1)

⦁ Ta có BD = EC (giả thiết)

Suy ra BD + DE = DE + EC.

Khi đó BE = CD.

Vì vậy phương án A đúng.

⦁ Xét ∆ABE và ∆ACD, có:

AB = AC (giả thiết)

AD = AE (giả thiết)

BE = CD (chứng minh trên)

Do đó ∆ABE = ∆ACD (c.c.c)

Vì vậy phương án B đúng.

⦁ Ta có ∆ABE = ∆ACD (chứng minh trên)

Suy ra $\hat{E A B} = \hat{D A C}$ (cặp góc tương ứng)

Do đó phương án C đúng.

Vậy ta chọn phương án D.

Câu 2:

Cho hình vẽ sau. Biết AB // CD và AD // BC.

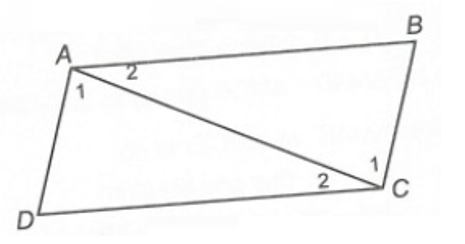
Cho hình vẽ sau. Biết AB song song CD và AD song song BC. Hình vẽ trên có mấy (ảnh 1)

Hình vẽ trên có mấy cặp tam giác bằng nhau?

A. 0;

B. 1;

C. 2;

D. 3.

Xem đáp án

Hướng dẫn giải

Đáp án đúng là: B

Xét ∆ABC và ∆CDA, có:

AC là cạnh chung.

$\hat{A_{1}} = \hat{C_{1}}$ (do AD // BC và hai góc này ở vị trí so le trong)

$\hat{A_{2}} = \hat{C_{2}}$ (do AB // DC và hai góc này ở vị trí so le trong)

Do đó ∆ABC = ∆CDA (g.c.g)

Vậy có 1 cặp tam giác bằng nhau.

Do đó ta chọn phương án B.

Câu 3:

Cho ∆MNP có $\hat{M} = 80 °$ , biết $\hat{N} - \hat{P} = 40 °$ . Khi đó số đo của $\hat{N}$ bằng:

A. 75°;

B. 45°;

C. 70°;

D. 60°.

Xem đáp án

Hướng dẫn giải

Đáp án đúng là: C

Ta có $\hat{N} - \hat{P} = 40 °$ . Suy ra $\hat{P} = \hat{N} - 40 °$ .

∆MNP có $\hat{M} + \hat{N} + \hat{P} = 180 °$ (định lí tổng ba góc trong một tam giác)

Suy ra $80 ° + \hat{N} + \hat{N} - 40 ° = 180 °$ .

Do đó $2 \hat{N} = 180 ° - 80 ° + 40 ° = 140 °$ .

Vì vậy $\hat{N} = 140 ° : 2 = 70 °$ .

Vậy ta chọn phương án C.

Câu 4:

Cho ∆ABC và ∆MNP bằng nhau. Biết số đo các góc như hình vẽ sau:

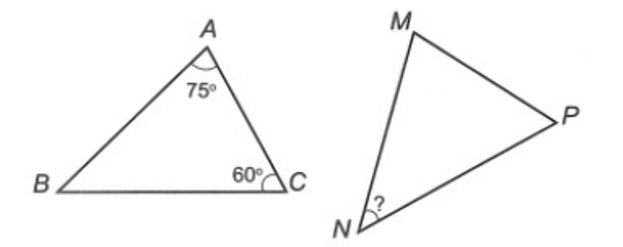
Cho tam giác ABC và tam giác MNP bằng nhau. Biết số đo các góc như hình vẽ sau: (ảnh 1)

Số đo của $\hat{M N P}$ bằng:

A. 60°;

B. 45°;

C. 30°;

D. 75°.

Xem đáp án

Hướng dẫn giải

Đáp án đúng là: B

∆ABC có: $\hat{A} + \hat{B} + \hat{C} = 180 °$ (định lí tổng ba góc trong một tam giác)

Suy ra $\hat{B} = 180 ° - \hat{A} - \hat{C} = 180 ° - 75 ° - 60 ° = 45 °$ .

Ta có ∆ABC = ∆MNP (giả thiết)

Suy ra $\hat{N} = \hat{B} = 45 °$ (cặp góc tương ứng)

Vậy ta chọn phương án B.

Câu 5:

Cho hình vẽ bên.

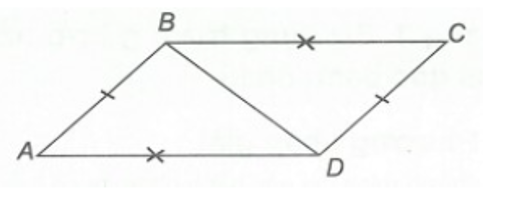
Kết luận nào sau đây đúng?

A. ∆ABD = ∆BCD;

B. ∆BAD = ∆CDB;

C. ∆ABD = ∆CBD;

D. ∆ABD = ∆CDB.

Xem đáp án

Hướng dẫn giải

Đáp án đúng là: D

Xét ∆ABD và ∆CDB, có:

BD là cạnh chung.

AB = CD (giả thiết)

AD = CB (giả thiết)

Do đó ∆ABD = ∆CDB (c.c.c)

Vậy ta chọn phương án D.

Câu 6:

Cho hình bên.

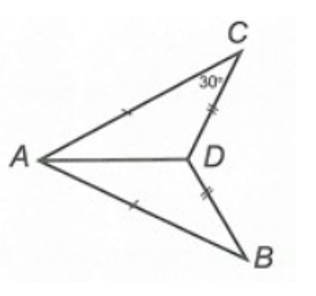
Số đo của $\hat{A B D}$ bằng:

A. 30°;

B. 45°;

C. 60°;

D. 85°.

Xem đáp án

Hướng dẫn giải

Đáp án đúng là: A

Xét ∆ADB và ∆ADC, có:

AD là cạnh chung.

AB = AC (giả thiết)

DB = DC (giả thiết)

Do đó ∆ADB = ∆ADC (c.c.c)

Suy ra $\hat{A B D} = \hat{A C D} = 30 °$ (cặp góc tương ứng)

Vậy ta chọn phương án A.

Câu 7:

Cho ∆ABC có AB = AC. Gọi AM là tia phân giác của $\hat{A}$ (M ∈ BC). Kẻ MD vuông góc AB (D ∈ AB) và ME vuông góc với AC (E ∈ AC).

Cho các khẳng định sau:

(I) $\hat{B M D} = \hat{C M E}$ ;

(II) ∆MBD = ∆MCE;

(III) AD = AE ;

Gọi m là số kết luận đúng và n là số kết luận sai. Giá trị của m và n là:

A. m = 0 và n = 1;

B. m = 2 và n = 1;

C. m = 3 và n = 0;

D. m = 1 và n = 2.

Xem đáp án

Hướng dẫn giải

Đáp án đúng là: C

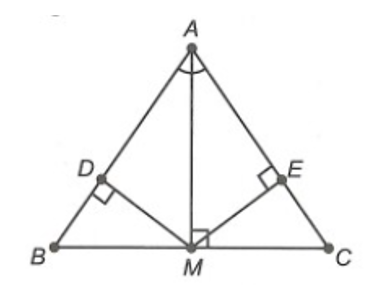
Cho tam giác ABC có AB = AC. Gọi AM là tia phân giác của góc A (M thuộc BC). (ảnh 1)

Xét ∆AMD và ∆AME, có:

AM là cạnh chung.

$\hat{A D M} = \hat{A E M} = 90 °$ .

$\hat{D A M} = \hat{E A M}$ (AM là phân giác của $\hat{D A E}$ )

Do đó ∆AMD = ∆AME (cạnh huyền – góc nhọn)

Suy ra AD = AE và MD = ME (các cặp cạnh tương ứng)

Do đó (III) đúng.

Ta có AB = AC (giả thiết) và AD = AE (chứng minh trên)

Suy ra AB – AD = AC – AE.

Khi đó DB = EC.

Xét ∆MBD và ∆MCE, có:

$\hat{B D M} = \hat{C E M} = 90 °$ .

DB = EC (chứng minh trên)

MD = ME (chứng minh trên)

Do đó ∆MBD = ∆MCE (c.g.c). Do đó (II) đúng.

Suy ra $\hat{B M D} = \hat{C M E}$ (cặp góc tương ứng). Do đó (I) đúng.

Vậy ta có 3 phát biểu đúng và 0 phát biểu sai hay m = 3 và n = 0.

Vậy ta chọn phương án C.

Câu 8:

Cho tam giác ABC có AD vuông góc với BC. Biết AB = AC = 3cm, $\hat{A} = 60 °$ . Tính cạnh BC.

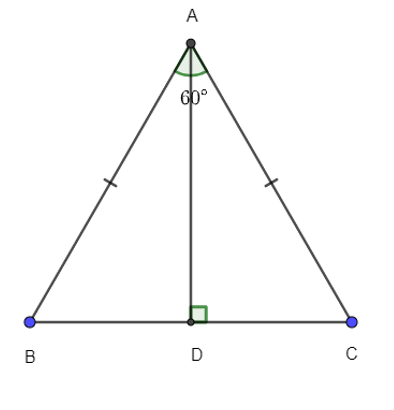
Cho tam giác ABC có AD vuông góc với BC. Biết AB = AC = 3cm, góc A=60 độ (ảnh 1)

A. BC = 6 cm;

B. BC = 1,5 cm;

C. BC = 9 cm;

D. BC = 3cm.

Xem đáp án

Hướng dẫn giải

Đáp án đúng là: D

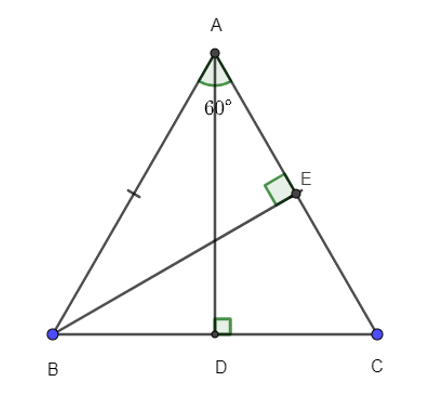
Cho tam giác ABC có AD vuông góc với BC. Biết AB = AC = 3cm, góc A=60 độ (ảnh 2)

Xét ∆ADB và ∆ADC, có:

AD là cạnh chung.

$\hat{A D B} = \hat{A D C} = 90 °$ .

DB = DC (giả thiết)

Do đó ∆ADB = ∆ADC (c.g.c)

$\Rightarrow \hat{A B D} = \hat{A C D}$ (cặp góc tương ứng)

Xét tam giác ABC, có: $\hat{A B D} + \hat{A C D} + \hat{B A C} = 180 °$ (định lí tổng ba góc trong tam giác)

$\Rightarrow \hat{A B D} = \hat{A C D} = \frac{180 ° - \hat{B A C}}{2} = \frac{180 ° - 60 °}{2} = 60 °$ .

Kẻ BE vuông góc với AC.

Xét ∆BEA và ∆BEC, có:

$\hat{B E A} = \hat{B E C} = 90 °$

BE là cạnh chung

$\hat{A B E} = \hat{C B E} = 90 ° - 60 ° = 30 °$

Do đó ∆BEA = ∆BEC (cạnh góc vuông – góc nhọn)

Suy ra AB = BC

Mà AB = 3cm nên BC = 3cm.

Vậy chọn đáp án D.

Câu 9:

Cho ∆ABC có AB = AC ( $\hat{A} < 90 °$ ). Kẻ BD vuông góc với AC (D ∈ AC) và CE vuông góc với AB (E ∈ AB). Gọi H là giao điểm của BD và CE.

Cho bảng sau:

A	B
a. ∆AEC	1. ∆HDC
b. ∆HEB	2. ∆CDB
c. ∆BEC	3. ∆ADB

Ghép các ý ở cột A với cột B để được một đẳng thức đúng?

A. a – 2; b – 1; c – 3;

B. a – 1; b – 3; c – 2;

C. a – 3; b – 1; c – 2;

D. a – 2; c – 1; b – 3.

Xem đáp án

Hướng dẫn giải

Đáp án đúng là: C

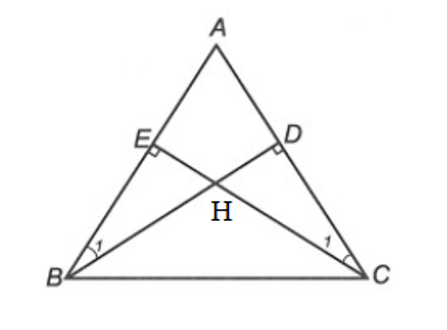
Cho tam giác ABC có AB = AC (góc A< 90 độ). Kẻ BD vuông góc với AC (D thuộc AC) và CE (ảnh 1)

+) Xét ∆ADB và ∆AEC, có:

AB = AC (giả thiết)

$\hat{A D B} = \hat{A E C} = 90 °$ .

$\hat{B A C}$ là góc chung.

Do đó ∆ADB = ∆AEC (cạnh huyền – góc nhọn)

Khi đó a – 3.

+) Vì ∆ADB = ∆AEC nên $\hat{B_{1}} = \hat{C_{1}}$ (cặp góc tương ứng) và AD = BE (cặp cạnh tương ứng)

Ta có: AD + DC = AC, AE + EB = AB

Mà AB = AC, AD = BE nên DC = EB.

Xét ∆HEB và ∆HDC, có:

$\hat{H E B} = \hat{H D C} = 90 °$

BE = DC

$\hat{B_{1}} = \hat{C_{1}}$

Suy ra ∆HEB = ∆HDC (g – c – g)

Do đó b – 1.

+) Xét ∆BEC và ∆CDB, có:

$\hat{B E C} = \hat{C D B} = 90 °$

BE = DC

BC là cạnh chung

Suy ra ∆BEC = ∆CDB (cạnh góc vuông – cạnh huyền)

Do đó c – 2.

Vậy a – 3, b – 1, c – 2.

Chọn đáp án C.

Câu 10:

Cho hình chữ nhật ABCD, M là trung điểm của cạnh BC. Kết luận nào sau đây sai?

A. AM = DM;

B. ∆ABM = ∆ADM ;

C. $\hat{M A D} = \hat{M D A}$ ;

D. A, B, C sai.

Xem đáp án

Hướng dẫn giải

Đáp án đúng là: D

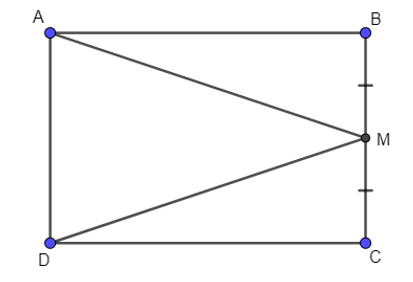
Cho hình chữ nhật ABCD, M là trung điểm của cạnh BC. Kết luận nào sau đây sai? (ảnh 1)

Xét ∆ABM và ∆DCM, có:

AB = DC (ABCD là hình chữ nhật)

$\hat{A B M} = \hat{D C M} = 90 °$ (ABCD là hình chữ nhật)

MB = MC (giả thiết)

Do đó ∆ABM = ∆DCM (c.g.c)

Suy ra AM = DM và $\hat{B A M} = \hat{C D M}$ (cặp cạnh và cặp góc tương ứng)

Ta có: $\hat{M A D} + \hat{B A M} = \hat{M D A} + \hat{C D M} = 90 °$ (các cặp góc phụ nhau)

Suy ra $\hat{M A D} = \hat{M D A}$

Vì vậy phương án A, B, C đều đúng.

Vậy ta chọn phương án D.

Câu 11:

Cho hình vẽ bên.

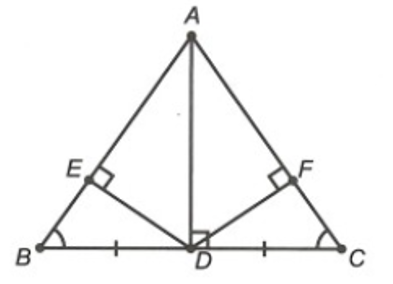
Khẳng định nào sau đây sai?

A. ∆AED = ∆AFD;

B. ∆BED = ∆CFD;

C. ∆ADB = ∆ADC;

D. ∆ADE = ∆AFD.

Xem đáp án

Hướng dẫn giải

Đáp án đúng là: D

⦁ Xét phương án B:

Xét ∆BED và ∆CFD, có:

$\hat{B E D} = \hat{C F D} = 90 °$ .

BD = CD (giả thiết)

$\hat{E B D} = \hat{F C D}$ (giả thiết)

Do đó ∆BED = ∆CFD (cạnh huyền – góc nhọn)

Vì vậy phương án B đúng.

⦁ Xét ∆AED và ∆AFD, có:

AD là cạnh chung.

ED = FD (∆BED = ∆CFD)

$\hat{A E D} = \hat{A F D} = 90 °$ .

Do đó ∆AED = ∆AFD (cạnh huyền – cạnh góc vuông)

Vì vậy phương án A đúng, phương án D sai (do viết sai thứ tự các đỉnh).

⦁ Xét phương án C:

Xét ∆ADB và ∆ADC, có:

AD là cạnh chung.

$\hat{A D B} = \hat{A D C} = 90 °$ .

DB = DC (giả thiết)

Do đó ∆ADB = ∆ADC (c.g.c)

Vì vậy phương án C đúng.

Vậy ta chọn phương án D.

Câu 12:

Cho ∆ABC vuông tại A có hai đường trung trực của hai cạnh AB và AC cắt nhau tại D. Vị trí của điểm D là

A. D là trung điểm BC;

B. D là trung điểm của AB;

C. D là trung điểm của AC;

D. D là điểm trong tam giác ABC.

Xem đáp án

Hướng dẫn giải

Đáp án đúng là: A

Gọi điểm M là giao điểm của đường trung trực của AB với BC.

Vì M thuộc trung trực của đoạn thẳng AB nên MA = MB.

Suy ra tam giác MAB cân tại M

⇒ $\hat{B} = \hat{M A B} \hat{B} = \hat{M A B}$

Ta có: $\hat{B} + \hat{C} = 90 °$ và $\hat{M A B} + \hat{M A C} = 90 °$

⇒ $\hat{C} = \hat{M A C}$

⇒ Tam giác MAC cân tại M

⇒ MA = MC ⇒ M thuộc đường trung trực của đoạn thẳng AC

Vậy M là giao điểm của hai đường trung trực của AB và AC hay ta có M trùng D.

Ta có DA = DB, DA = DC nên DB = DC

Vậy D là trung điểm của đoạn thẳng BC.

Câu 13:

Cho tam giác ABC cân tại A, có $\hat{A} = 24 °$ . Trên tia đối của tia BC lấy điểm D sao cho $\hat{A D B} = 30 °$ , trên tia đối của tia CB lấy điểm E sao cho BD = CE. Tính $\hat{B A E}$ ?

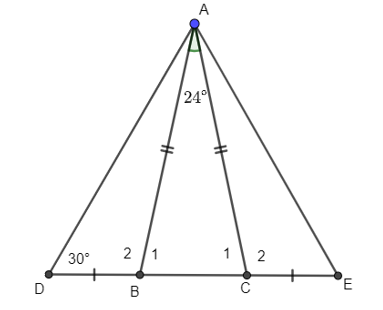
Cho tam giác ABC cân tại A, có góc A= 24 độ . Trên tia đối của tia BC lấy điểm D sao cho (ảnh 1)

A. $\hat{A B E} = 72 °$

B. $\hat{A B E} = 48 °$

C. $\hat{A B E} = 78 °$

D. $\hat{A B E} = 68 °$

Xem đáp án

Hướng dẫn giải

Đáp án đúng là: A

Ta có $\hat{B_{1}} + \hat{B_{2}} = 180 °$ (hai góc kề bù) và $\hat{C_{1}} + \hat{C_{2}} = 180 °$ (hai góc kề bù)

Mà $\hat{B_{1}} = \hat{C_{1}}$ (∆ABC cân tại A)

Suy ra $\hat{B_{2}} = \hat{C_{2}}$ .

Xét ∆ABD và ∆ACE, có:

BD = CE (giả thiết)

$\hat{B_{2}} = \hat{C_{2}}$ (chứng minh trên)

AB = AC (giả thiết)

Do đó ∆ABD = ∆ACE (c – g – c)

⇒ $\hat{D} = \hat{E} = 30 °$ (cặp góc tương ứng)

Xét tam giác ABE, có:

$\hat{B A E} + \hat{B_{1}} + \hat{E} = 180 °$ (định lí tổng ba góc trong tam giác)

$\hat{B A E} = 180 ° - \hat{B_{1}} - \hat{E} = 180 ° - 78 ° - 30 ° = 72 °$

Vậy ta chọn phương án A.

Câu 14:

Cho đoạn thẳng CD. Gọi A là trung điểm của CD. Kẻ một đường thẳng vuông góc với CD tại A. Trên đường thẳng đó, lấy điểm B sao cho $\hat{B C D} = 60 °$ . Khi đó ∆BCD là tam giác gì?

A. Tam giác tù;

B. Tam giác đều;

C. Tam giác vuông cân;

D. Tam giác vuông.

Xem đáp án

Hướng dẫn giải

Đáp án đúng là: B

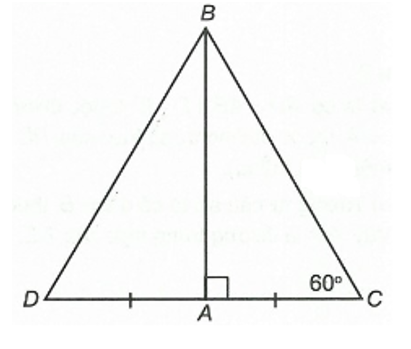
Cho đoạn thẳng CD. Gọi A là trung điểm của CD. Kẻ một đường thẳng vuông góc (ảnh 1)

Ta có AC = AD (A là trung điểm của CD) và AB ⊥ CD (giả thiết)

Suy ra AB là đường trung trực của đoạn thẳng CD.

Do đó BD = BC (tính chất đường trung trực của một đoạn thẳng)

Vì vậy ∆BCD cân tại B.

Mà ∆BCD có $\hat{C} = 60 °$ (giả thiết)

Do đó ∆BCD là tam giác đều.

Vậy ta chọn phương án B.

Câu 15:

Cho ∆ABC có $\hat{B} = 2 \hat{C}$ . Kẻ đường phân giác BD, từ D kẻ DE //BC (E ∈ AB). Số tam giác cân là:

A. 0

B. 1

C. 2

D. 3

Xem đáp án

Hướng dẫn giải

Đáp án đúng là: C

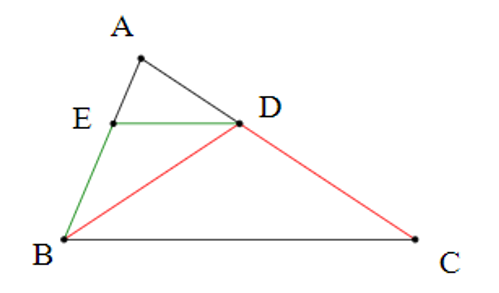
Cho tam giác ABC có góc B= 2 góc C. Kẻ đường phân giác BD, từ D kẻ DE song songBC (E thuộc AB). (ảnh 1)

∆ABC có BD là đường phân giác.

Suy ra $\hat{A B D} = \hat{D B C} = \frac{1}{2} \hat{B A C} = \frac{1}{2} .2 \hat{A C B} = \hat{A C B}$ .

Do đó ∆BCD cân tại D.

Ta có BD // BC (giả thiết)

Suy ra $\hat{E D B} = \hat{D B C}$ (cặp góc so le trong)

Mà $\hat{E D B} = \hat{D B C}$ (chứng minh trên)

Do đó $\hat{E D B} = \hat{E B D}$ .

Suy ra ∆BED cân tại E.

Do đó có 2 tam giác cân

Vậy ta chọn phương án C.