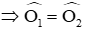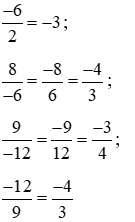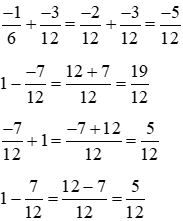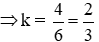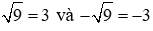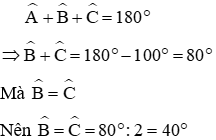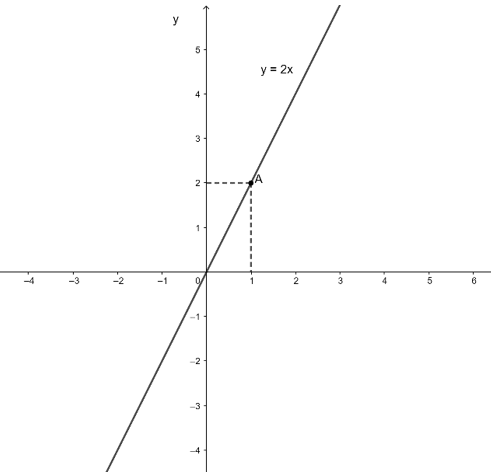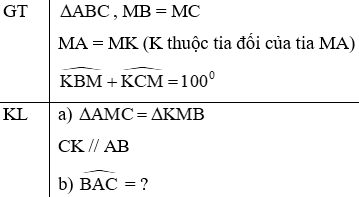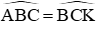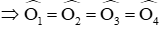13 câu hỏi trắc nghiệm thuộc Đề thi Toán lớp 7 Học kì 1 có đáp án (Đề 2)

Đề thi Toán lớp 7 Học kì 1 có đáp án

Đề thi Toán lớp 7 Học kì 1 có đáp án (Đề 2)

10114 lượt thi
13 câu hỏi
90 phút

BẮT ĐẦU LÀM BÀI

Danh sách câu hỏi

Câu 1:

I -Trắc nghiệm:

Hãy chọn câu trả lời đúng nhất.

Trong các phân số sau, phân số nào biểu diễn số hữu tỷ $\frac{- 3}{4}$ ?

A. $\frac{- 6}{2}$

B. $\frac{8}{- 6}$

C. $\frac{9}{- 12}$

D. $\frac{- 12}{9}$

Xem đáp án

Chọn đáp án C

Câu 2:

Số $\frac{- 5}{12}$ là kết quả của phép tính:

A. $- \frac{1}{6} + - \frac{3}{12}$

B. $1 - \frac{- 7}{12}$

C. $1 + \frac{- 7}{12}$

D. $1 - \frac{7}{12}$

Xem đáp án

Chọn đáp án A

Câu 3:

Cho x và y là hai đại lượng tỉ lệ thuận và x = 6 thì y = 4. Hệ số tỉ lệ k của y đối với x là:

A. 24

B. $\frac{3}{- 2}$

C. $\frac{1}{24}$

D. $\frac{2}{3}$

Xem đáp án

Vì x và y là hai đại lượng tỉ lệ thuận nên ta có y = kx

Với x = 6 thì y = 4 nên thay vào ta được: 4 = k.6

Chọn đáp án D

Câu 4:

Căn bậc hai của 9 bằng:

A. 3

B. -3

C. 3 và -3

D. 81

Xem đáp án

9 có hai căn bậc hai là

Chọn đáp án C

Câu 5:

Cách viết nào dưới đây là đúng?

A. |-0,55| = -0,55

B. |-0,55| = 0,55

C. -|-0,55| = 0,55

D. -|0,55| = 0,55

Xem đáp án

Ta có: |-0,55| = 0,55 ; -|-0,55| = -0,55; -|0,55| = -0,55

Chọn đáp án B

Câu 6:

Kết quả của phép tính $(- 5)^{2} . (- 5)^{3}$ là:

A. $(- 5)^{5}$

B. $(- 5)^{6}$

C. $(25)^{6}$

D. $(25)^{5}$

Xem đáp án

Ta có: $(- 5)^{2} . (- 5)^{3} = {(- 5)}^{2 + 3} = (- 5)^{5}$

Chọn đáp án A

Câu 7:

Tam giác ABC có $\hat{B} = \hat{C}$ và $\hat{A} = 100 °$ . Góc B bằng:

A. $80 °$

B. $60 °$

C. $50 °$

D. $40 °$

Xem đáp án

Theo định lý tổng ba góc trong tam giác ABC ta có:

Chọn đáp án D

Câu 8:

Hai đường thẳng song song là hai đường thẳng:

A. Có ít nhất hai điểm chung.

B. Không có điểm chung.

C. Không vuông góc với nhau.

D. Chỉ có một điểm chung.

Xem đáp án

Hai đường thẳng song song là hai đường thẳng không có điểm chung (định nghĩa hai đường thẳng song song).

Chọn đáp án B

Câu 9:

II-Tự luận

Thực hiện phép tính.

a) A = $(- \frac{4}{5} + \frac{2}{3}) . \frac{7}{11} + (- \frac{1}{5} + \frac{1}{3}) . \frac{7}{11}$

b) $B = (- 3)^{2} . (\frac{3}{4} - 0, 25) - | - 2 |$

Xem đáp án

Câu 10:

Cho hàm số y = f(x) = (m + 1)x.

a) Tìm m để f(2) = 4.

b)Vẽ đồ thị hàm số với m tìm được.

Xem đáp án

a) Ta có f(2) = 4

Thay x = 2 vào hàm số ta được: (m + 1).2 = 4

⇒ m + 1 = 2 ⇒ m = 1

Vậy m = 1 thì f(2) = 4.

b) Với m =1 thì ta có hàm số: y = f(x) = 2x

Lấy x = 1 thì y = 2.1 = 2 nên điểm A(1; 2) thuộc đồ thị hàm số y = 2x

Vậy đồ thị hàm số y = 2x là đường thẳng OA.

Câu 11:

Tìm x, y, z biết:

a) $|x - \frac{2}{5}| = \frac{3}{4}$

b) $\frac{x}{5} = \frac{y}{3} = \frac{z}{4}$ và x +2y -z = 14

Xem đáp án

Áp dụng tính chất dãy tỉ số bằng nhau ta có:

Vậy x =10; y = 6; z = 8

Câu 12:

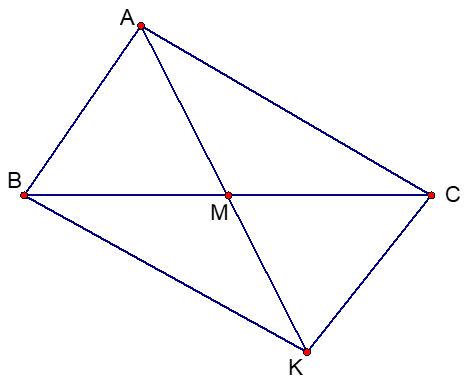
Cho tam giác ABC. Gọi M là trung điểm của BC. Trên tia đối của MA lấy điểm K sao cho MK = MA.

a) Chứng minh ΔAMC = ΔKMB và CK song song AB.

b) Biết $\hat{K B M} + \hat{K C M} = 100 °$ . Tính $\hat{B A C}$

Xem đáp án

Chứng minh

a) Xét tam giác AMC và KMB có:

AM = MK (gt)

MB = MC (M là trung điểm của BC)

(hai góc đối đỉnh)

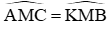
Do đó: ΔAMC = ΔKMB(c.g.c)

Chứng minh tương tự ta cũng có: ΔAMB = ΔKMC (c.g.c)

Suy ra:

Mà hai góc này ở vị trí so le trong

Nên CK // AB

b) Chứng minh được ΔABC = ΔKCB (c.c.c)

Xét ΔKBC có:

Câu 13:

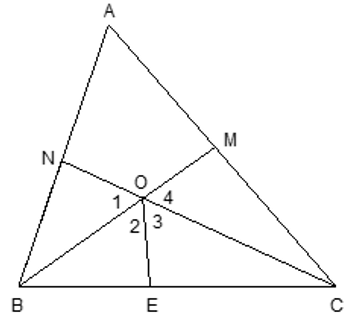
Cho tam giác ABC. Tia phân giác của góc B cắt AC tại M. Tia phân giác của góc C cắt AB tại N. Giả sử BN + CM = BC. Hãy tính số đó góc A.

Xem đáp án

Gọi BM giao CN là O. Trên cạnh BC lấy điểm E sao cho BN = BE mà BN + CM = BC (gt) ⇒ CE = CM.

Ta chứng minh ΔBNO = ΔBEO (c.g.c) . Chứng minh tương tự . Mà (hai góc đối đỉnh)

Bắt đầu thi ngay