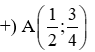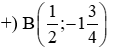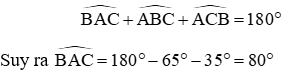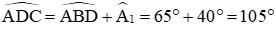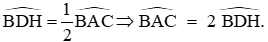Đề thi Toán lớp 7 Học kì 1 có đáp án (Đề 3)
-
10008 lượt thi
-
12 câu hỏi
-
90 phút
Danh sách câu hỏi
Câu 2:
Cho hàm số . Điểm nào sau đây thuộc đồ thị hàm số trên:
Xem đáp án
Thay lần lượt tọa độ của các điểm ở đáp án vào hàm số:
Ta có: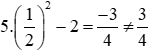 
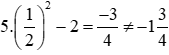
nên điểm A không thuộc đồ thị hàm số
nên điểm B không thuộc đồ thị hàm số
+) C(2; -18)
nên điểm C không thuộc đồ thị hàm số
+) D(-1; 3)
nên điểm D thuộc đồ thị hàm số .
Chọn đáp án D
Câu 3:
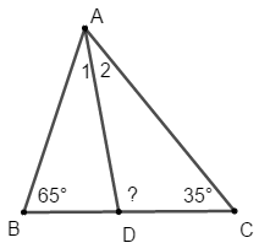
Cho ΔABC có . Tia phân giác của cắt BC tại D.
Số đo là:
Xem đáp án
Theo định lý tổng ba góc trong tam giác ABC ta có:
Ta có: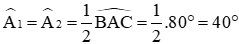 
(AD là tia phân giác trong góc BAC)
Lại có góc ADC là góc ngoài tại đỉnh D của tam giác ABD nên theo tính chất góc ngoài của tam giác ta có: 
Chọn đáp án B
Câu 4:
Cho ΔABC = ΔMNP. Biết AB = 10 cm, MP = 8 cm, NP = 7 cm. Chu vi của ΔABC là:
Xem đáp án
Ta có: ΔABC = ΔMNP
Suy ra: AB = MN = 10 cm; BC = NP = 7 cm; AC = MP = 8 cm.
Chu vi tam giác ABC là: AB + BC + AC = 10 + 7 + 8 = 25 cm.
Chọn đáp án B
Câu 5:
II-Tự luận:
Xác định tính Đúng/Sai của các khẳng định sau:
1. Nếu x tỉ lệ thuận với y theo hệ số tỉ lệ 2 thì y cũng tỉ lệ thuận với x theo hệ số tỉ lệ là 2.
2. Trên mặt phẳng tọa độ, tất cả các điểm có hoành độ bằng 0 đều nằm trên trục tung.
3. Nếu hai cạnh và một góc xen giữa của tam giác này bằng hai cạnh và một góc xen giữa của tam giác kia thì hai tam giác đó bằng nhau.
4. Mỗi góc ngoài của tam giác bằng tổng 2 góc trong không kề với nó của tam giác đó.
Xem đáp án
1. Sai. Nếu x tỉ lệ thuận với y theo hệ số tỉ lệ 2 thì y cũng tỉ lệ thuận với x theo hệ số tỉ lệ là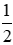 
.
2. Sai. Điểm O(0; 0) có hoành độ là 0 vừa thuộc trục hoành, và vừa thuộc trục tung.
3. Đúng theo trường hợp bằng nhau thứ hai của tam giác.
4. Đúng theo định lý góc ngoài của tam giác.
Câu 9:
Để làm một công việc trong 8 giờ cần 35 công nhân. Nếu có 40 công nhân cùng làm thì công việc đó được hoàn thành trong mấy giờ? (Năng suất các công nhân là như nhau)
Xem đáp án
Gọi thời gian để 40 công nhân hoàn thành công việc đó là (giờ) với 0 < x < 8
Vì cùng làm một công việc và năng suất các công nhân là như nhau nên số công nhân tỉ lệ nghịch với thời gian hoàn thành công việc, do đó ta có:
Vậy 40 công nhân thì hoàn thành công việc đó trong 7 giờ
Câu 10:
Cho hàm số y = a.x (a ≠ 0). Biết rằng đồ thị của hàm số đó đi qua điểm A(-4; 1).
a. Hãy xác định hệ số a;
b. Các điểm M(4 ;-1) và N(2;3) có thuộc đồ thị của hàm số trên không? Vì sao?
Xem đáp án
a) Vì đồ thị của hàm số y = a.x (a ≠ 0) đi qua điểm A(-4 ;1) nên ta có:
Vậy với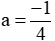 
thì đồ thị của hàm số y = a.x (a ≠ 0) đi qua điểm A(-4; 1)
Câu 11:
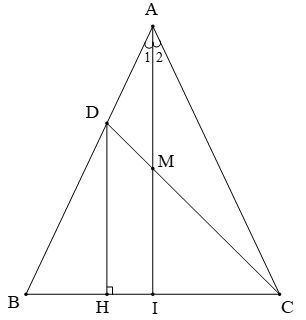
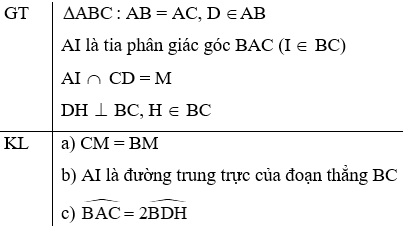
Cho có AB = AC; D là điểm bất kì trên cạnh AB. Tia phân giác của góc A cắt cạnh DC ở M, cắt cạnh BC ở I.
a) Chứng minh CM = BM.
b) Chứng minh AI là đường trung trực của đoạn thẳng BC.
c) Từ D kẻ DH ⊥ BC (H ∈ BC). Chứng minh .
Xem đáp án
a) Xét ΔABM và ΔACM có:
AB = AC (gt)
(AI là tia phân giác của góc BAC)
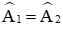
AM cạnh chung
Do đó ΔABM = ΔACM (c.g.c).
Suy ra BM = CM (hai cạnh tương ứng)
b) Xét ΔABI và ΔACI có:
AB = AC (gt)
(AI là tia phân giác của góc BAC)
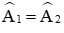
AI là cạnh chung.
Do đó ΔABI = ΔACI (c.g.c).
Suy ra BI = CI (hai cạnh tương ứng). (1)
và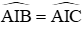 
(hai góc tương ứng).
+ Mà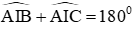 
(Vì là hai góc kề bù).
Nên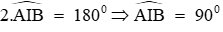 
suy ra AI ⊥ BC tại I. (2)
Từ (1) và (2) suy ra AI là đường trung trực của đoạn thẳng BC.
c)
+ Ta có: DH ⊥ BC (GT).
AI ⊥ BC(chứng minh trên)
Suy ra DH // AI (quan hệ giữa tính vuông góc với tính song song)
( vì là hai góc đồng vị ). (3)
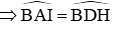
+ Ta lại có: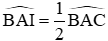 
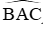
(vì AI là tia phân giác của 
).(4)
Từ (3) và (4) suy ra 
Câu 12:
Tìm giá trị nhỏ nhất của biểu thức: A = 3.|1 - 2x| - 5
Xem đáp án
Vậy GTNN của biểu thức A là -5 đạt được khi 