Đề kiểm tra Giữa kì 2 Toán 7 có đáp án (Mới nhất) - Đề 3
-
1348 lượt thi
-
7 câu hỏi
-
45 phút
Danh sách câu hỏi
Câu 1:
Xác định tính đúng/sai của các khẳng định sau bằn cách đánh dấu “x” vào ô trống thích hợp trong bảng sau:
|
STT |
Câu |
Đúng |
Sai |
|
1 |
Tam giác có ba cạnh 12cm; 16cm; 20cm là tam giác vuông. |
|
|
|
2 |
Tam giác đều là tam giác cân có một góc bằng 60o. |
|
|
|
3 |
Trong tam giác, góc đối diện với cạnh lớn nhất là góc tù. |
|
|
|
4 |
Trong tam giác cân, góc ở đáy luôn nhỏ hơn 90o. |
|
|
 Xem đáp án
Xem đáp án
Xác định tính đúng/sai của các khẳng định sau bằn cách đánh dấu “x” vào ô trống thích hợp trong bảng sau:
- Xét câu 1.
Ta có: 122 + 162 = 144 + 256 = 400; 202 = 400.
Ta thấy 122 + 162 = 202 nên tam giác có ba cạnh 12cm; 16cm; 20cm là tam giác vuông (theo định lý Py-ta-go đảo).
Do đó câu 1 đúng.
- Xét câu 2: Tam giác đều là tam giác cân có một góc bằng 60o (dấu hiệu nhận biết tam giác đều).
Do đó câu 2 đúng.
- Xét câu 3.
+ Trong tam giác tù, góc đối diện với cạnh lớn nhất là góc tù.
+ Trong tam giác vuông, góc đối diện với cạnh lớn nhất là góc vuông.
+ Trong tam giác nhọn, góc đối diện với cạnh lớn nhất là góc lớn nhất.
Do đó câu 3 sai.
- Xét câu 4.
Tổng ba góc của một tam giác bằng 180o nên:
Trong tam giác cân, tổng hai góc ở đáy và góc ở đỉnh bằng 180o.
Suy ra: tổng hai góc ở đáy nhỏ hơn 180o.
Mà trong tam giác cân có hai góc ở đáy bằng nhau nên góc ở đáy nhỏ hơn 90o.
Do đó câu 4 đúng.
Vậy ta có bảng sau:
|
STT |
Câu |
Đúng |
Sai |
|
1 |
Tam giác có ba cạnh 12cm; 16cm; 20cm là tam giác vuông. |
x |
|
|
2 |
Tam giác đều là tam giác cân có một góc bằng 60o. |
x |
|
|
3 |
Trong tam giác, góc đối diện với cạnh lớn nhất là góc tù. |
|
x |
|
4 |
Trong tam giác cân, góc ở đáy luôn nhỏ hơn 90o. |
x |
|
Câu 2:
Cho hàm số \(f(x) = \frac{2}{3}x - 1\). Trong các điểm sau, điểm nào thuộc đồ thị hàm số trên.
 Xem đáp án
Xem đáp án
Thay x = 1 vào đồ thị hàm số \(y = f(x) = \frac{2}{3}x - 1\), ta được:
\(f(1) = \frac{2}{3}\,.\,1 - 1 = - \frac{1}{3} \ne \frac{1}{3}\).
Do đó, điểm \(A\left( {1;\,\,\frac{1}{3}} \right)\) không thuộc đồ thị hàm số \(y = f(x) = \frac{2}{3}x - 1\).
Và điểm \(B\left( {1;\,\, - \frac{1}{3}} \right)\) thuộc đồ thị hàm số \(y = f(x) = \frac{2}{3}x - 1\).
Thay x = −3 vào đồ thị hàm số \(y = f(x) = \frac{2}{3}x - 1\), ta được:
\(f( - 3) = \frac{2}{3}\,.\,( - 3) - 1 = - 3 \ne 1\).
Do đó, điểm C(−3; 1) không thuộc đồ thị hàm số \(y = f(x) = \frac{2}{3}x - 1\).
Thay x = 6 vào đồ thị hàm số \(y = f(x) = \frac{2}{3}x - 1\), ta được:
\(f(6) = \frac{2}{3}\,.\,6 - 1 = 3 \ne - 3\).
Do đó, điểm D(6; −3) không thuộc đồ thị hàm số \(y = f(x) = \frac{2}{3}x - 1\).
Vậy chọn B.
Câu 3:
 Xem đáp án
Xem đáp án
Thay x = – 1 vào biểu thức 2(x2 – 1) + 3x – 2, ta được:
2.[(–1)2 – 1] + 3.(–1) – 2 = 2.0 – 3 – 2 = –5.
Vậy chọn D.
Câu 4:
Điểm bài kiểm tra môn Toán học kỳ I của 32 học sinh lớp 7A được ghi trong bảng sau:
|
7 |
4 |
4 |
6 |
6 |
4 |
6 |
8 |
|
8 |
7 |
2 |
6 |
4 |
8 |
5 |
6 |
|
9 |
8 |
4 |
7 |
9 |
5 |
5 |
5 |
|
7 |
2 |
7 |
6 |
7 |
8 |
6 |
10 |
a) Dấu hiệu ở đây là gì?
b) Lập bảng “tần số” và nhận xét.
c) Tính số trung bình cộng và tìm mốt của dấu hiệu.
d) Vẽ biểu đồ đoạn thẳng.
 Xem đáp án
Xem đáp án
a) Dấu hiệu: Điểm kiểm tra môn toán của mỗi học sinh lớp 7A.
b) Bảng “tần số”:
|
Điểm (x) |
2 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
|
Tần số (n) |
2 |
5 |
4 |
7 |
6 |
5 |
2 |
1 |
N = 32 |
* Nhận xét:
- Số các giá trị của dấu hiệu: 32.
- Số các giá trị khác nhau của dấu hiệu: 9.
- Điểm kiểm tra cao nhất: 10 điểm
- Điểm kiểm tra thấp nhất: 2 điểm
- Đa số học sinh được điểm từ 7 đến 9.
c)
* Số trung bình cộng:
\(\overline X = \frac{{2\,.\,2 + 4\,.\,5 + 5\,.\,4 + 6\,.\,7 + 7\,.\,6 + 8\,.\,5 + 9\,.\,2 + 10\,.\,1}}{{32}} = \frac{{196}}{{32}} = 6,125\) (điểm).
* Mốt của dấu hiệu: M0 = 7
d) Biểu đồ đoạn thẳng:
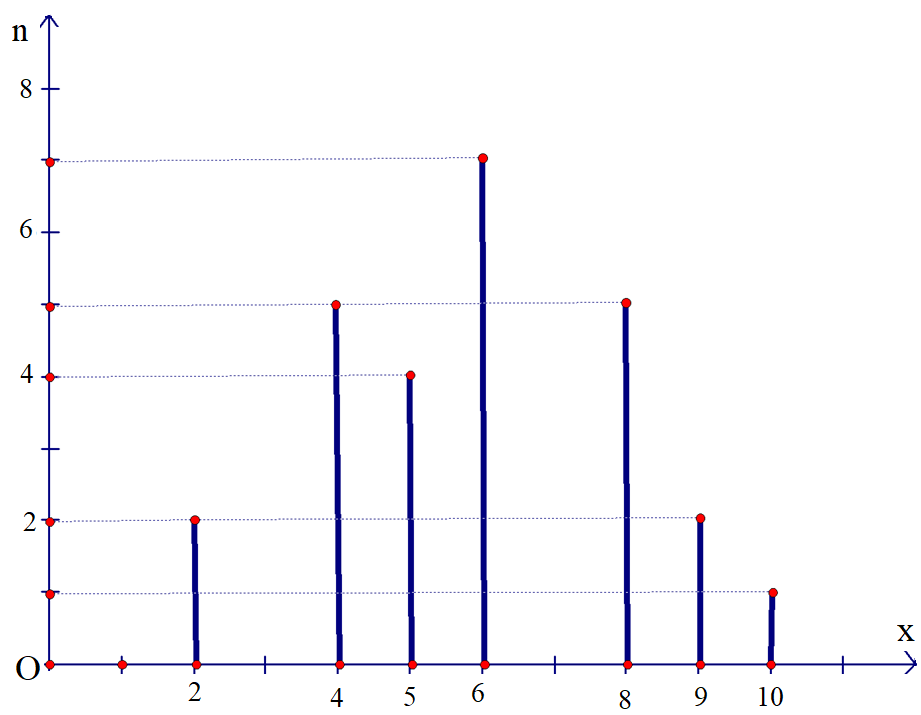
Câu 5:
Điểm bài kiểm tra môn Toán học kỳ I của 32 học sinh lớp 7A được ghi trong bảng sau:
|
7 |
4 |
4 |
6 |
6 |
4 |
6 |
8 |
|
8 |
7 |
2 |
6 |
4 |
8 |
5 |
6 |
|
9 |
8 |
4 |
7 |
9 |
5 |
5 |
5 |
|
7 |
2 |
7 |
6 |
7 |
8 |
6 |
10 |
a) Dấu hiệu ở đây là gì?
b) Lập bảng “tần số” và nhận xét.
c) Tính số trung bình cộng và tìm mốt của dấu hiệu.
d) Vẽ biểu đồ đoạn thẳng.
 Xem đáp án
Xem đáp án
a) Dấu hiệu: Điểm kiểm tra môn toán của mỗi học sinh lớp 7A.
b) Bảng “tần số”:
|
Điểm (x) |
2 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
|
Tần số (n) |
2 |
5 |
4 |
7 |
6 |
5 |
2 |
1 |
N = 32 |
* Nhận xét:
- Số các giá trị của dấu hiệu: 32.
- Số các giá trị khác nhau của dấu hiệu: 9.
- Điểm kiểm tra cao nhất: 10 điểm
- Điểm kiểm tra thấp nhất: 2 điểm
- Đa số học sinh được điểm từ 7 đến 9.
c)
* Số trung bình cộng:
\(\overline X = \frac{{2\,.\,2 + 4\,.\,5 + 5\,.\,4 + 6\,.\,7 + 7\,.\,6 + 8\,.\,5 + 9\,.\,2 + 10\,.\,1}}{{32}} = \frac{{196}}{{32}} = 6,125\) (điểm).
* Mốt của dấu hiệu: M0 = 7
d) Biểu đồ đoạn thẳng:

Câu 6:
Cho ΔABC cân tại A kẻ AH\[ \bot \]BC (H\[ \in \]BC).
a) Chứng minh: HB = HC.
b) Kẻ HD\[ \bot \]AB (D\[ \in \]AB), HE\[ \bot \]AC (E\[ \in \]AC). Chứng minh ΔHDE cân.
c) Cho \(\widehat {BAC} = {120^o}\) thì ΔHDE trở thành tam giác gì? Vì sao?
 Xem đáp án
Xem đáp án
|
GT |
ΔABC cân tại A; AH\[ \bot \]BC (H\[ \in \]BC); HD\[ \bot \]AB (D\[ \in \]AB), HE\[ \bot \]AC (E\[ \in \]AC). |
|
KL |
a) Chứng minh: HB = HC. b) ΔHDE cân. c) Cho \(\widehat {BAC} = {120^o}\) thì ΔHDE trở thành tam giác gì? Vì sao? |
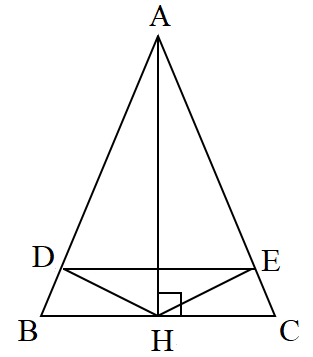
a) Xét ΔABC cân tại A có AH là đường cao (vì AH\[ \bot \]BC) nên AH cũng là đường trung tuyến.
Do đó HB = HC.
b) Xét ΔBDH vuông tại D và ΔCEH vuông tại E có:
HB = HC (cmt)
\(\widehat B = \widehat C\) (ΔABC cân tại A)
Do đó ΔBDH = ΔCEH (cạnh huyền - góc nhọn).
Suy ra DH = HE (hai cạnh tương ứng)
Suy ra ΔHDE cân tại H.
Mặt khác, vì \(\widehat A = {120^o}\) nên \(\widehat B = \widehat C = \frac{1}{2}\,.\,({180^o} - \widehat A) = \frac{1}{2}\,.\,{60^o} = {30^o}\).
Từ ΔBDH = ΔCEH (cmt) suy ra \(\widehat {BHD} = \widehat {CHE}\) (hai góc tương ứng).
Xét ΔBDH vuông tại D nên \(\widehat B + \widehat {BHD} = {90^o} \Rightarrow \widehat {BHD} = {90^o} - \widehat B = {60^o}\).
Do đó \(\widehat {BHD} = \widehat {CHE} = {60^o}\)
Ta có:\(\widehat {BHC} = \widehat {BHD} + \widehat {DHE} + \widehat {EHC}\)
Suy ra \(\widehat {DHE} = \widehat {BHC} - \left( {\widehat {BHD} + \widehat {CHE}} \right)\)
\( \Rightarrow \widehat {AHE} = {180^o} - ({60^o} + {60^o}) = {60^o}\).
Ta thấy ΔHED cân tại H có \(\widehat {AHE} = {60^o}\)nên ΔHED là tam giác đều.
Câu 7:
Tìm giá trị nhỏ nhất của biểu thức \[{\left[ {{{\left( {x + \frac{1}{2}} \right)}^2} + \frac{5}{4}} \right]^2}\].
 Xem đáp án
Xem đáp án
Ta có \[{\left( {x + \frac{1}{2}} \right)^2} \ge 0\,\,\forall x \Rightarrow {\left( {x + \frac{1}{2}} \right)^2} + \frac{5}{4} \ge \frac{5}{4}\,\,\forall x\]
\[A = {\left[ {{{\left( {x + \frac{1}{2}} \right)}^2} + \frac{5}{4}} \right]^2} \ge {\left( {\frac{5}{4}} \right)^2} = \frac{{25}}{{16}}\,\,\forall x\]
Dấu “=” xảy ra khi và chỉ khi \[x = - \frac{1}{2}\].
Vậy giá trị nhỏ nhất của biểu thức A là \[\frac{{25}}{{16}}\] khi \[x = - \frac{1}{2}\].
