Đề kiểm tra 1 tiết Toán 7 Chương 3 Hình học có đáp án (Trắc nghiệm - Tự luận 1)
-
9429 lượt thi
-
11 câu hỏi
-
50 phút
Danh sách câu hỏi
Câu 1:
A. Phần trắc nghiệm (3 điểm)
Trong mỗi câu dưới đây, hãy chọn phương án trả lời đúng:
Bộ ba số nào sau đây không thể là độ dài ba cạnh của một tam giác?
Xem đáp án
Ta có: 6 + 7 = 13 không thỏa mãn bất đẳng thức tam giác nên chọn B
Câu 2:
Tam giác ABC có độ dài hai cạnh là BC = 1cm, AC = 8cm. Tìm AB biết độ dài cạnh AB là một số nguyên.
Xem đáp án
Ta có AC - BC < AB < AC + BC ⇒ 7 < AB < 9 ⇒ AB = 8cm.
Chọn C
Câu 5:
Cho tam giác ABC có Tia AD là tia phân giác của góc (BAC) (D ∈ BC). Khi đó số đo của góc (ADB) là:
Xem đáp án
Ta có ∠A = 180o - 45o - 75o = 60o. Vì AD là tia phân giác nên
∠(BAD) = 30o
Trong tam giác ADB có ∠(ADB) = 180o - 45o - 30o = 105o. Chọn A
Câu 6:
B. Phần tự luận (7 điểm)
Cho tam giác ABC vuông tại A có AB = 6cm, AC = 8cm.
a. Tính độ dài cạnh BC
Xem đáp án
a. Áp dụng định lí Pytago trong tam giác ABC ta có:
BC2 = AB2 + AC2 = 62 + 82 = 100 ⇒ BC = 10cm
Câu 7:
Cho tam giác ABC vuông tại A có AB = 6cm, AC = 8cm.
b. So sánh các góc của tam giác ABC
Xem đáp án
b. Vì AB < AC < BC ⇒ ∠C < ∠B < ∠A (quan hệ giữa góc và cạnh đối diện trong tam giác)
Câu 8:
Cho tam giác ABC vuông tại A, tia phân giác của (ABC) cắt AC tại D. Kẻ DE ⊥ BC (E ∈ BC). Gọi F là giao điểm của BA và ED. Chứng minh:
a. ∆ABD = ∆EBD
Xem đáp án
a. Hình vẽ (0.5 điểm)
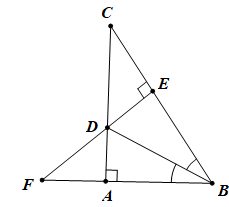
Xét ∆ABD và ∆EBD có:
∠(ABD) = ∠(DBE)
BD là cạnh chung
⇒ ∆ABD = ∆EBD(cạnh huyền – góc nhọn) (1 điểm)
Câu 9:
Cho tam giác ABC vuông tại A, tia phân giác của (ABC) cắt AC tại D. Kẻ DE ⊥ BC (E ∈ BC). Gọi F là giao điểm của BA và ED. Chứng minh:
b. BD là đường trung trực của AE
Xem đáp án
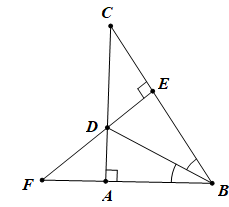
b. Ta có AB = BE ⇒ B nằm trên đường trung trực của AE (0.5 điểm)
Do ∆ABD = ∆EBD nên AD = DE (hai cạnh tương ứng)
⇒ D nằm trên đường trung trực của AE
Vậy BD là đường trung trực của AE (0.5 điểm)
Câu 10:
Cho tam giác ABC vuông tại A, tia phân giác của (ABC) cắt AC tại D. Kẻ DE ⊥ BC (E ∈ BC). Gọi F là giao điểm của BA và ED. Chứng minh:
c. DF = DC
Xem đáp án
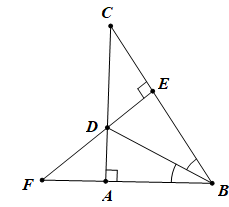
c. Xét ∆ADF và ∆EDC có:
AD = DE
∠(ADF) = ∠(EDC) (hai góc đối đỉnh)
⇒ ∆ADF = ∆EDC ( cạnh góc vuông – góc nhọn kề)(1 điểm)
⇒ DF = DC (hai cạnh tương ứng) (0.5 điểm)
Câu 11:
Cho tam giác ABC vuông tại A, tia phân giác của (ABC) cắt AC tại D. Kẻ DE ⊥ BC (E ∈ BC). Gọi F là giao điểm của BA và ED. Chứng minh:
d. AD < DC
Xem đáp án
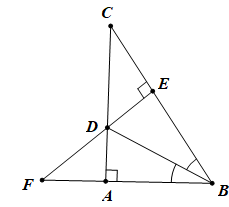
d. Trong tam giác vuông DEC có DC là cạnh huyên nên DC là cạnh lớn nhất
⇒ DC > DE mà DE = AD ⇒ DC > AD (1 điểm)