Dạng 1. Khẳng định có tồn tại hay không một tam giác khi biết độ dài ba đoạn thẳng
-
142 lượt thi
-
10 câu hỏi
-
45 phút
Danh sách câu hỏi
Câu 1:
Bộ ba độ dài nào sau đây có thể là độ dài ba cạnh của một tam giác?
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: D
Ta có:
⦁ 8 > 3 + 4, không thỏa mãn bất đẳng thức tam giác;
⦁ 13 > 5 + 7, không thỏa mãn bất đẳng thức tam giác;
⦁ 9 – 5 > 3, không thỏa mãn bất đẳng thức tam giác;
⦁ 5 – 2 < 4 < 5 + 2 nên bộ ba độ dài 2 cm; 4 cm; 5 cm có thể là độ dài ba cạnh của một tam giác.
Vậy ta chọn phương án D.
Câu 2:
Với bộ ba đọan thẳng dưới đây, bộ ba nào không thể là ba cạnh của một tam giác?
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: B
Ta có 12 > 6 + 5 không thỏa mãn bất đẳng thức tam giác;
Nên bộ ba độ dài 12 cm; 6 cm; 5 cm không thể là ba cạnh của một tam giác.
Câu 3:
Bộ ba độ dài nào sau đây có thể là độ dài ba cạnh của một tam giác?
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: A
Ta có:
⦁ 8 – 5 < 10 < 8 + 5 nên bộ ba độ dài 8 cm; 5 cm; 10 cm có thể là độ dài ba cạnh của một tam giác;
⦁ 11 + 9 = 20, không thỏa mãn bất đẳng thức tam giác;
⦁ 6 > 4 + 1, không thỏa mãn bất đẳng thức tam giác;
⦁ 8 + 4 < 15, không thỏa mãn bất đẳng thức tam giác.
Vậy ta chọn phương án A.
Câu 4:
Cho một tam giác cân có độ dài hai cạnh là 3,9 cm và 7,9 cm. Chu vi của tam giác đó là
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: C
Cạnh thứ ba của tam giác cân có độ dài bằng một trong hai cạnh kia.
Loại trường hợp độ dài cạnh thứ ba bằng 3,9 cm vì 3,9 + 3,9 = 7,8 < 7,9, không thỏa mãn bất đẳng thức tam giác.
Trường hợp độ dài cạnh thứ ba bằng 7,9 cm thỏa mãn vì 7,9 + 3,9 > 7,9, thỏa mãn bất đẳng thức tam giác.
Vậy chu vi của tam giác đó là: 7,9 + 7,9 + 3,9 = 19,7 (cm).
Câu 5:
Cho tam giác MNP có MN = 2 cm và MP = 5 cm. Độ dài của cạnh NP là
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: C
Áp dụng bất đẳng thức tam giác cho ∆MNP, ta có:
MP – MN < NP < MP + MN
5 – 2 < NP < 5 + 2
3 < NP < 7
Dựa vào các phương án, ta thấy chỉ có phương án NP = 4 cm thỏa mãn.
Câu 6:
Cho tam giác ABC có cạnh AB = 5 cm và AC = 8 cm. Biết độ dài cạnh BC là một số tự nhiên chẵn. Độ dài cạnh BC là
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: A
Theo bất đẳng thức tam giác, ta có:
AC – AB < BC < AC + AB
8 – 5 < BC < 8 + 5
3 < BC < 13
Vì độ dài cạnh BC là một số tự nhiên chẵn nên BC = 10 cm.
Câu 7:
Cho tam giác ABC có cạnh AB = 5 cm và AC = 8 cm. Có bao nhiêu giá trị nguyên lẻ thỏa mãn cho độ dài cạnh của BC?
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: A
Đặt BC = x (cm) (x ∈ ℕ* và x là số lẻ).
Theo bất đẳng thức tam giác, ta có:
AC – AB < BC < AC + AB
8 – 5 < x < 8 + 5
3 < x < 13
Vì độ dài cạnh BC là một số tự nguyên lẻ nên x ∈ {5; 7; 9; 11}.
Vậy có 4 giá trị nguyên lẻ thỏa mãn yêu cầu.
Câu 8:
Có bao nhiêu tam giác có độ dài hai cạnh là 12 cm và 9 cm còn độ dài cạnh thứ ba là một số nguyên chia hết cho 3?
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: A
Gọi độ dài cạnh thứ ba của tam giác là x (x > 0, cm).
Áp dụng bất đẳng thức tam giác, ta có:
12 – 9 < x < 12 + 9
3 < x < 21
Vì x là số nguyên nên x ∈ {4; 5; ... ; 20; 21}
Mặt khác, x chia hết cho 3 suy ra x ∈ {6; 9; 12; 15; 18; 21}.
Vậy có 6 tam giác thỏa mãn.
Câu 9:
Ba vị trí của nhà Mai, nhà Lan và trường học được mô tả như hình vẽ dưới đây.
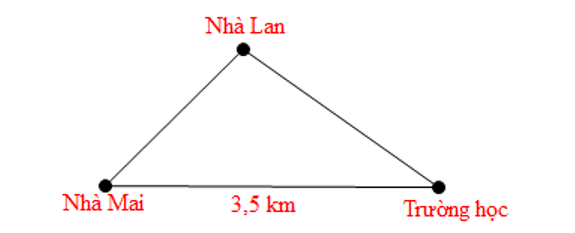
Trong buổi sáng hôm nay, Mai phải đến nhà Lan để lấy đồ trước khi đến trường.
Bạn Mai nói rằng tổng quãng đường mà Mai đã đi khoảng 3 km.
Bạn Lan nói rằng tổng quãng đường mà Mai đã đi khoảng 4 km.
Bạn Minh nói rằng tổng quãng đường mà Mai đã đi khoảng 5 km.
Khẳng định nào sau đây là đúng?
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: A
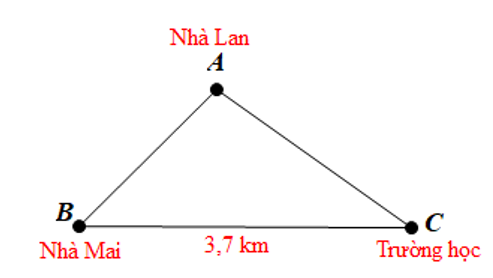
Đặt ba điểm A, B, C tại ba vị trí như hình vẽ trên.
Theo bất đẳng thức ta có: AB + AC > BC
Nên AB + AC > 3,7 cm.
Do đó tổng quãng đường từ nhà Mai đến nhà Lan rồi từ nhà Lan tới trường học phải lớn hơn 3,7 km.
Vậy nên bạn Mai đã nói sai, ta chọn phương án A.
Câu 10:
Cho hình
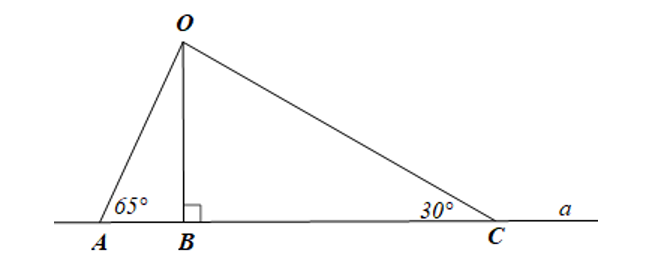
Khẳng định nào sau đây là đúng?
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: A
Vì OB là đường vuông góc kẻ từ điểm O đến đường thẳng a;
OA, OC là các đường xiên kẻ từ O đến đường thẳng a.
Nên OB < OA; OB < OC (1)
Xét ∆OAC có (vì 65° > 30°)
Suy ra: OC > OA (quan hệ giữa góc và cạnh đối diện trong tam giác) (2)
Từ (1) và (2) suy ra: OB < OA < OC.
Vậy ta chọn phương án A.