Trắc nghiệm Toán 7 CD Bài 8. Đường vuông góc và đường xiên (Thông hiểu) có đáp án
-
1206 lượt thi
-
7 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 1:
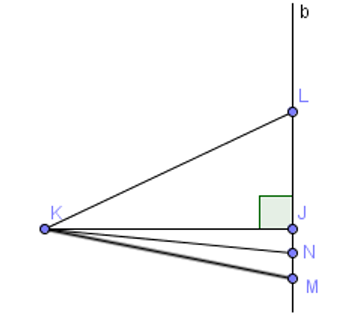
Cho hình vẽ dưới đây. Trong các đoạn thẳng KL, KJ, KN và KM. Đoạn thẳng ngắn nhất là
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: B
Do các đoạn thẳng KL, KN, KM là các đường xiên kẻ từ điểm K đến đường thẳng b.
Đoạn thẳng KJ là đường vuông góc kẻ từ điểm K đến đường thẳng b.
Nên đoạn thẳng KJ là đoạn thẳng ngắn nhất.
Câu 2:
Cho hình vẽ dưới đây. Biết
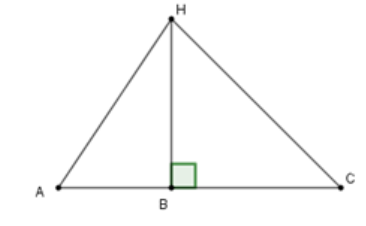
So sánh đúng là
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: C
Do các đoạn thẳng CH và AH các đường xiên kẻ từ điểm H đến đường thẳng AC và thẳng BH là đường vuông góc kẻ từ điểm H đến đường thẳng AC.
Suy ra BH < AH và BH < CH.
Xét tam giác HAC có (giả thiết) suy ra CH > AH
Do đó BH < AH < CH.
Câu 3:
Cho tam giác MNP nhọn. H là hình chiếu của P trên MN. K là hình chiếu của H trên MP. So sánh nào dưới đây đúng?
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: A
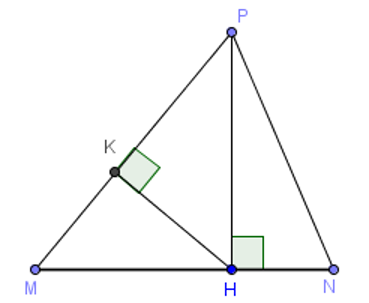
Ta có HK là đường vuông góc kẻ từ điểm H đến PM và HP là đường xiên kẻ từ H đến PM. Do đó HK < HP.
Ta có PH là đường vuông góc kẻ từ điểm P đến MN và PN là đường xiên kẻ từ P đến MN. Do đó PH < PN
Suy ra KH < HP < PN.
Câu 4:
Cho tam giác ABC có AD là khoảng cách từ A đến BC và BE là khoảng cách từ E đến AC. So sánh nào dưới đây đúng?
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: C
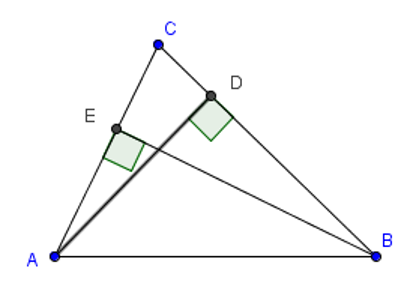
Ta có BC là đường xiên từ điểm B đến AC nên BE < BC (quan hệ đường vuông góc – đường xiên).
Có: AC là đường xiên từ điểm A đến BC nên AD < AC (quan hệ đường vuông góc – đường xiên).
Do đó: AD + BE < AC + BC.
Câu 5:
Cho tam giác PMN có D là hình chiếu của M trên PN, E là hình chiếu của N trên PM. So sánh nào dưới đây đúng?
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: A
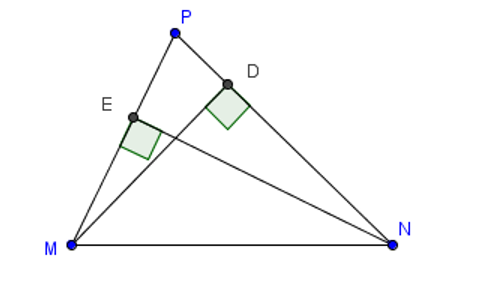
D là hình chiếu của M trên PN (giả thiết) nên MD là đường vuông góc từ M đến PN
Mà MN là đường xiên từ M đến PN.
Suy ra MD < MN (quan hệ đường vuông góc – đường xiên)
E là hình chiếu của N trên PM (giả thiết) nên NE là đường vuông góc từ N đến PM
Mà MN là đường xiên từ N đến PM.
Suy ra NE < MN (quan hệ đường vuông góc – đường xiên)
Do đó MD + NE < MN + MN = 2MN
Hay MD + NE < 2MN.
Câu 6:
Cho tam giác ABC vuông tại A. Gọi M là trung điểm của AC, D và E theo thứ tự là hình chiếu của A và Ctrên đường thẳng BM. So sánh AB với BD + BE là
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: C
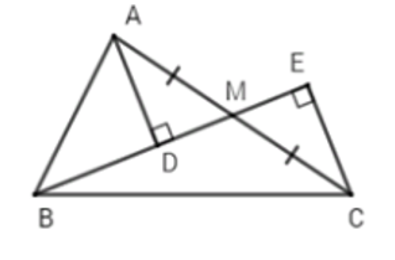
Vì tam giác BAM vuông tại A nên AB < BM (quan hệ giữa đường vuông góc và đường xiên)
Mà BM = BD + DM ⇒ BA < BD + DM(1)
Mặt khác: BM = BE – ME ⇒ BA < BE – ME (2)
Cộng hai vế cùa (1) và (2) ta được: 2BA < BD + BE + MD – ME (3)
Vì M là trung điểm của AC nên AM = MC
Xét hai tam giác vuông ADM và CEM có:
AM = CM (chứng minh trên)
(đối đỉnh)
Suy ra ∆ADM = ∆CEM (cạnh huyền – góc nhọn)
Do đó DM = ME (hai cạnh tương ứng) (4)
Từ (3) và (4) suy ra: 2AB < BD + BE.
Câu 7:
Cho tam giác ABC vuông tại C (AC < BC), CH ⊥ AB (H ∈ AB). Trên các cạnh AB và AC lấy tương ứng hai điểm M và N sao cho BM = BC, CN = CH. Chọn câu đúng nhất.
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: D
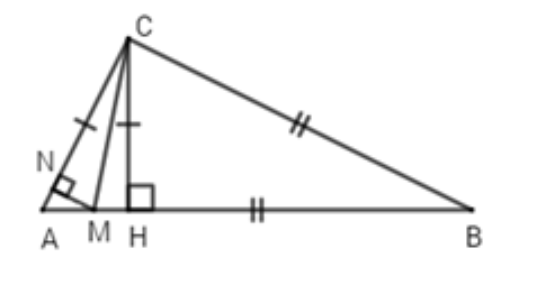
Ta có: BM = BC (giả thiết) ⇒ ∆BMC cân tại B (1)
Lại có: và (2)
Từ (1), (2)
Xét ∆MCH và ∆MCN có:
MN là cạnh chung
(chứng minh trên)
CH = CN (giả thiết)
Suy ra ∆MCH và ∆MCN (c.g.c)
(2 góc tương ứng). Do đó MN ⊥ AC.
Xét ∆AMN có AN là đường vuông góc hạ từ A xuống MN (chứng minh trên) và AM là đường xiên.
Suy ra AN < AM
Mà BM = BC; CH = CN (giả thiết)
Suy ra: BM + MA + CH > BC + NA + CN
Do đó: BA + CH > BC + AC.