6 câu hỏi trắc nghiệm thuộc Đề kiểm tra học kì 1 Toán 7 có đáp án ( Mới nhất)_ Đề số 6

Câu 1:

Thực hiện các phép tính (bằng cách hợp lý nếu có):

a) $\frac{2}{7} + (\frac{- 17}{7} + \frac{8}{7})$

b) $8 : (\frac{- 3}{5}) - 6 : (\frac{- 3}{5})$

c) $\frac{2^{15} . 9^{3}}{6^{7} . 4^{4}}$

Xem đáp án

a) $\frac{2}{7} + (\frac{- 17}{7} + \frac{8}{7})$

$= \frac{2}{7} + \frac{- 17}{7} + \frac{8}{7}$

$= \frac{2 + (- 17) + 8}{7}$

$= \frac{- 7}{7} = - 1$ .

b) $8 : (\frac{- 3}{5}) - 6 : (\frac{- 3}{5})$

$= (8 - 6) : \frac{- 3}{5}$

$= 2 : \frac{- 3}{5}$

$= 2 . \frac{- 5}{3} = \frac{- 10}{3}$ .

c) $\frac{2^{15} . 9^{3}}{6^{7} . 4^{4}}$

$= \frac{2^{15} . 3^{6}}{2^{7} . 3^{7} . 2^{8}}$

$= \frac{2^{15} . 3^{6}}{2^{15} . 3^{7}} = \frac{1}{3}$ .

Câu 2:

Tìm x biết:

a) $x + \frac{3}{2} = 5,6$

b) $x : \frac{1}{2} = \frac{5}{4} : \frac{19}{8}$

c) $| x - \frac{1}{2} | = \frac{5}{4}$

Xem đáp án

a) $x + \frac{3}{2} = 5,6$

x + 1,5 = 5,6

x = 5,6 − 1,5

x = 4,1

Vậy x = 4,1.

b) $x : \frac{1}{2} = \frac{5}{4} : \frac{19}{8}$

$x : \frac{1}{2} = \frac{10}{9}$

$x = \frac{10}{9} . \frac{1}{2}$

$x = \frac{5}{19}$

Vậy $x = \frac{5}{19}$ .

c) $| x - \frac{1}{2} | = \frac{5}{4}$

- Trường hợp 1: $x - \frac{1}{2} = \frac{5}{4}$

$x = \frac{5}{4} + \frac{1}{2}$

$x = \frac{7}{4}$ .

- Trường hợp 2: $x - \frac{1}{2} = - \frac{5}{4}$

$x = - \frac{5}{4} + \frac{1}{2}$

$x = \frac{- 3}{4}$ .

Vậy $x \in {\frac{7}{4}; \frac{- 3}{4}}$ .

Câu 3:

a) Tìm số học sinh của lớp 7A và lớp 7B, biết số học sinh của lớp 7B ít hơn 7A là 6 học sinh và tỉ số học sinh của lớp 7A và 7B là 7 : 6?

b) Cho biết 3 máy cày, cày xong một cánh đồng hết 30 giờ. Hỏi 5 máy cày (cùng năng suất) như thế cày xong cánh đồng đó hết bao nhiêu giờ?

Xem đáp án

a) Gọi x, y lần lượt là số học sinh lớp 7A và lớp 7B (học sinh) (x, y $\in ℕ *)$ .

Tỉ số học sinh của lớp 7A và 7B là 7 : 6 nên $\frac{x}{7} = \frac{y}{6}$ .

Vì số học sinh của lớp 7B ít hơn 7A là 6 học sinh nên x – y = 6.

Áp dụng tính chất dãy tỉ số bằng nhau, ta có:

$\frac{x}{7} = \frac{y}{6} = \frac{x - y}{7 - 6} = \frac{6}{1} = 6$

Do đó: x = 7 . 6 = 42; y = 6 . 6 = 36.

Vậy lớp 7A có 42 học sinh và lớp 7B có 36 học sinh.

b) Gọi x (giờ) là thời gian để 5 máy cày (cùng năng suất), cày xong cánh đồng (x > 0).

Làm việc trên cùng một cánh đồng nên số máy cày (cùng năng suất) và thời gian cày xong cánh đồng là hai đại lượng tỉ lệ nghịch.

Suy ra: $\frac{x}{30} = \frac{3}{5}$ .

Do đó $x = \frac{3 . 30}{5} = 18$ .

Vậy 5 máy cày (cùng năng suất) thì cày xong cánh đồng hết 18 giờ.

Câu 4:

Cho hàm số y = −3x.

a) Vẽ đồ thị của hàm số.

b) Tính giá trị của x (làm tròn đến chữ số thập phân thứ hai) khi y = 2.

Xem đáp án

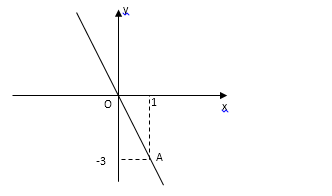
a) Vẽ đồ thị của hàm số y = −3x.

- Vẽ hệ trục tọa độ Oxy;

- Với x = 1 thì y = −3, ta được điểm A (1; −3) thuộc đồ thị hàm số y = −3x.

Do đó đường thẳng OA là đồ thị hàm số đã cho.

b) Thay y = 2 vào hàm số y = −3x, ta được:

−3x = 2

$x = \frac{2}{- 3} \approx - 0,67$ .

Vậy khi y = 2 thì x ≈ −0,67.

Câu 5:

1) Cho hình vẽ có ${\hat{A}}_{1} = 45^{o}, {\hat{B}}_{1} = 135^{o}$ .

1) Cho hình vẽ có A1 bằng 45 độ, B1 bằng 135 độ .a) Tính số đo góc A2? b) Chứng minh a // b.2) Cho tam giác ABC có AB = AC và tia phân giác góc A cắt BC ở H. a) Chứng minh ∆ABH = ∆ACH. b) Chứng minh c) Vẽ HD vuông góc với AB (D thuộc AB) và HE vuống góc AC ( E thuộc AC) . Chứng minh: DE // BC. (ảnh 1)

a) Tính số đo góc A₂?

b) Chứng minh a // b.

2) Cho tam giác ABC có AB = AC và tia phân giác góc A cắt BC ở H.

a) Chứng minh ∆ABH = ∆ACH.

b) Chứng minh $A H ⊥ B C$

c) Vẽ $H D ⊥ A B$ $(D \in A B)$ và $H E ⊥ A C$ $(E \in A C)$ . Chứng minh: DE // BC.

Xem đáp án

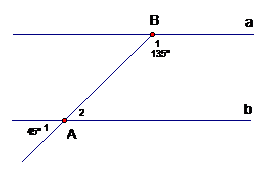
a) Vì ${\hat{A}}_{1}$ và ${\hat{A}}_{2}$ là hai góc đối đỉnh nên ${\hat{A}}_{1} = {\hat{A}}_{2} = 45^{o}$ .

Vậy ${\hat{A}}_{2} = 45^{o}$ .

b) Chứng minh a // b.

Ta có: ${\hat{A}}_{2} + {\hat{B}}_{1} = 45^{o} + 135^{o} = 180^{o}$

Mà ${\hat{A}}_{2}$ và ${\hat{B}}_{1}$ là cặp góc trong cùng phía.

Do đó a // b (đpcm).

2)

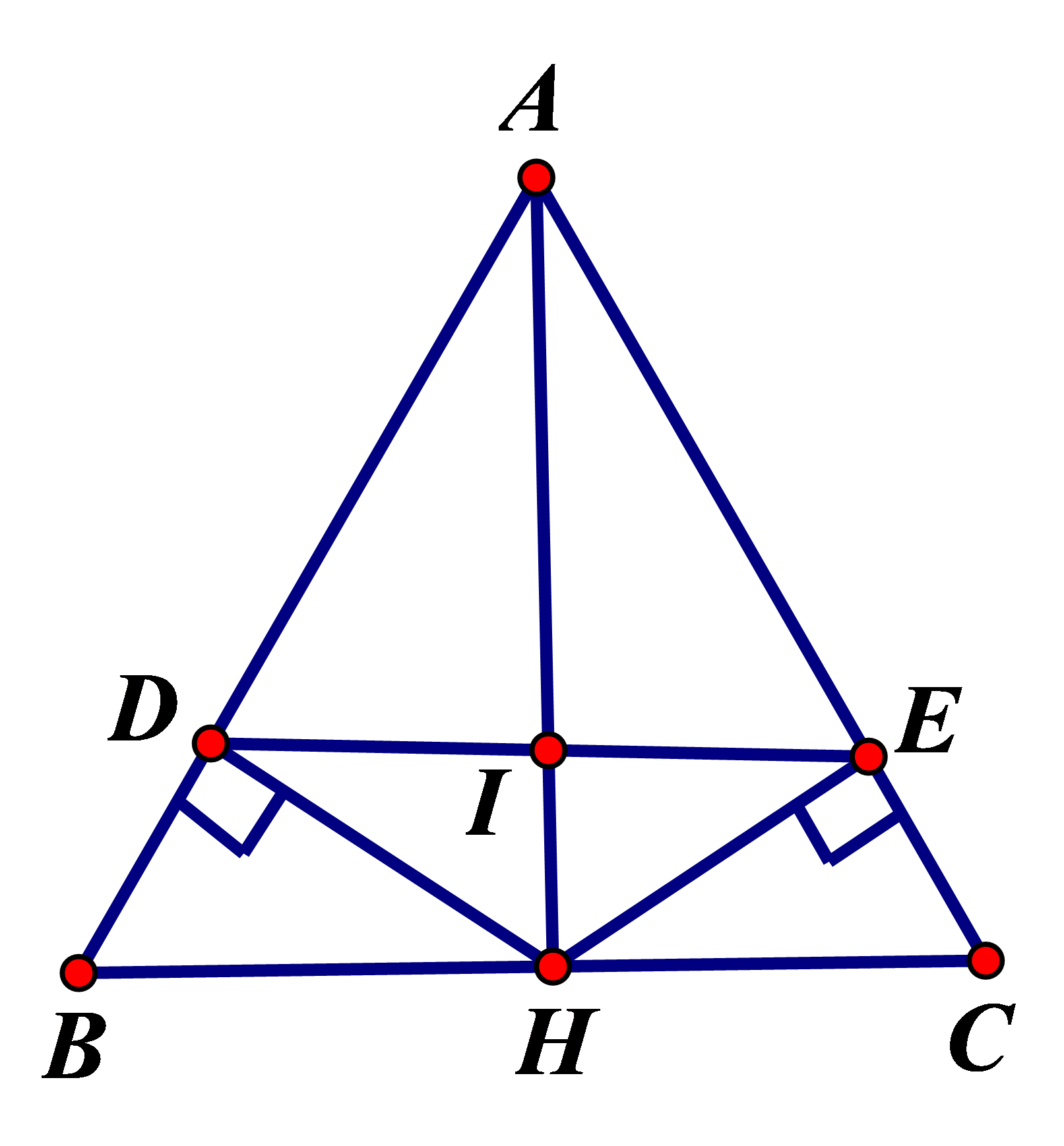
a) Chứng minh ∆ABH = ∆ACH

Xét ∆ABH và ∆ACH có:

AB = AC (gt)

$\hat{B A H} = \hat{C A H}$ (gt)

AH cạnh chung

Do đó ∆ABH = ∆ACH (c.g.c)

b) Chứng minh $A H ⊥ B C$

Vì ∆ABH = ∆ACH (câu a) nên $\hat{A H B} = \hat{A H C}$

Mà $\hat{A H B} + \hat{A H C}$ = 180^o (hai góc kề bù)

Suy ra: $\hat{A H B} = \hat{A H C}$ = 90^o.

Vậy AH $⊥$ BC.

c) Chứng minh: DE // BC.

Gọi I là giao điểm của AH và DE.

Xét ∆ADH vuông tại D và ∆AEH vuông tại E có:

$\hat{B A H} = \hat{C A H}$ (gt)

Cạnh AH chung

Do đó ∆ADH = ∆AEH (cạnh huyền – góc nhọn)

Suy ra AD = AE (hai cạnh tương ứng)

Xét ∆ADI và ∆AEI có:

AD = AE (cmt)

$\hat{B A H} = \hat{C A H}$ (vì AH là tia phân giác $\hat{A B C}$ )

Cạnh AI chung

Do đó ∆ADI = ∆AEI (c.g.c)

Suy ra $\hat{A I D} = \hat{A I E}$ (hai góc tương ứng)

Mà $\hat{A I D} + \hat{A I E}$ = 180^o (hai góc kề bù)

Suy ra: $\hat{A I D} = \hat{A I E}$ = 90^o hay AH vuông góc DE

Ta có: AH vuông góc BC và AH vuông góc DE (cmt)

Do đó DE // BC (quan hệ tính vuông góc với tính song song).

Câu 6:

Chứng minh rằng nếu $\frac{a}{b} = \frac{b}{c}$ thì:

$\frac{a^{2} + b^{2}}{b^{2} + c^{2}} = \frac{a}{c}$ (với b, c ≠ 0).

Xem đáp án

Ta có: $\frac{a}{b} = \frac{b}{c} \Rightarrow b^{2} = a . c$ (Tính chất tỉ lệ thức)

Lại có: $\frac{a}{b} = \frac{b}{c} \Rightarrow \frac{a^{2}}{b^{2}} = \frac{b^{2}}{c^{2}} = \frac{a^{2} + b^{2}}{b^{2} + c^{2}}$ (Tính chất dãy tỉ số bằng nhau)

Do đó: $\frac{a^{2} + b^{2}}{b^{2} + c^{2}} = \frac{b^{2}}{c^{2}} = \frac{a c}{c^{2}} = \frac{a}{c}$

Vậy $\frac{a^{2} + b^{2}}{b^{2} + c^{2}} = \frac{a}{c}$ .