6 câu hỏi trắc nghiệm thuộc Đề kiểm tra học kì 1 Toán 7 có đáp án ( Mới nhất)_ Đề số 5

Câu 1:

Thực hiện các phép tính (tính hợp lý nếu có thể)

a) $\frac{2}{3} \cdot (\frac{3}{4} - \frac{5}{7}) - \frac{1}{28} : (\frac{- 5}{6} + \frac{1}{3})$

b) $\frac{12}{37} + \frac{3}{21} + \frac{25}{37} - \frac{7}{14} + \frac{6}{7}$

Xem đáp án

a) $\frac{2}{3} \cdot (\frac{3}{4} - \frac{5}{7}) - \frac{1}{28} : (\frac{- 5}{6} + \frac{1}{3})$

$= \frac{2}{3} \cdot (\frac{21}{28} - \frac{20}{28}) - \frac{1}{28} : (\frac{- 5}{6} + \frac{2}{6})$

$= \frac{2}{3} \cdot \frac{1}{28} - \frac{1}{28} : (\frac{- 3}{6})$

$= \frac{2}{3} \cdot \frac{1}{28} + \frac{1}{28} \cdot 2$

$= \frac{1}{28} \cdot (\frac{2}{3} + 2)$

b) $\frac{12}{37} + \frac{3}{21} + \frac{25}{37} - \frac{7}{14} + \frac{6}{7}$

$= (\frac{12}{37} + \frac{25}{37}) + (\frac{3}{21} + \frac{6}{7}) - \frac{7}{14}$

$= \frac{37}{37} + (\frac{3}{21} + \frac{18}{21}) - \frac{1}{2}$

$= 1 + 1 - \frac{1}{2}$

$= 2 - \frac{1}{2} = \frac{3}{2}$ .

Câu 2:

Tìm x, biết:

a) $1 \frac{3}{2} - x = \frac{5}{3}$

b) $x : \frac{4}{3} = 2 \frac{1}{4} : \frac{1}{3}$

c) $| x - \frac{1}{2} | - \sqrt{25} = - 2$

Xem đáp án

a) $1 \frac{3}{2} - x = \frac{5}{3}$

$\frac{5}{2} - x = \frac{5}{3}$

$x = \frac{5}{2} - \frac{5}{3}$

$x = \frac{5}{6}$

Vậy $x = \frac{5}{6}$ .

b) $x : \frac{4}{3} = 2 \frac{1}{4} : \frac{1}{3}$

$x : \frac{4}{3} = \frac{9}{4} . 3$

$x : \frac{4}{3} = \frac{27}{4}$

$x = \frac{27}{4} . \frac{4}{3}$

x = 9.

Vậy x = 9.

c) $| x - \frac{1}{2} | - \sqrt{25} = - 2$

$| x - \frac{1}{2} | - 5 = - 2$

$| x - \frac{1}{2} | = 3$

- Trường hợp 1: $x - \frac{1}{2} = 3$

$x = 3 + \frac{1}{2}$

$x = \frac{7}{2}$ .

- Trường hợp 2: $x - \frac{1}{2} = - 3$

$x = - 3 + \frac{1}{2}$

$x = \frac{- 5}{2}$ .

Vậy $x \in {\frac{7}{2}; \frac{- 5}{2}}$ .

Câu 3:

Tìm a, b, c biết:

a) $\frac{a}{2} = \frac{b}{3} = \frac{c}{4}$ và a + b + c = 81.

b) Cho 2a = 3b; 4b = 5c và 2a + 3b – 4c = 56.

Xem đáp án

a) $\frac{a}{2} = \frac{b}{3} = \frac{c}{4}$ và a + b + c = 81.

Áp dụng tính chất dãy tỉ số bằng nhau, ta có:

$\frac{a}{2} = \frac{b}{3} = \frac{c}{4} = \frac{a + b + c}{2 + 3 + 4} = \frac{81}{9} = 9$

Do đó a = 9 . 2 = 18;

b = 9 . 3 = 27;

c = 9 . 4 = 36.

Vậy a = 18, b = 27, c = 36.

b) Cho 2a = 3b; 4b = 5c và 2a + 3b – 4c = 56.

Ta có 2a = 3b; 4b = 5c nên $\frac{a}{3} = \frac{b}{2}; \frac{b}{5} = \frac{c}{4}$

$\Rightarrow \frac{a}{15} = \frac{b}{10}; \frac{b}{10} = \frac{c}{8}$

$\Rightarrow \frac{a}{15} = \frac{b}{10} = \frac{c}{8}$

$\Rightarrow \frac{2 a}{30} = \frac{3 b}{30} = \frac{4 c}{32}$ .

Áp dụng tính chất dãy tỉ số bằng nhau, ta có:

$\frac{2 a}{30} = \frac{3 b}{30} = \frac{4 c}{32} = \frac{2 a + 3 b + 4 c}{30 + 30 + 32} = \frac{56}{28} = 2$ .

Do đó, 2a = 30 . 2 = 60 $\Rightarrow$ a = 30;

3b = 30 . 2 = 60 $\Rightarrow$ b = 20;

4c = 32 . 2 = 64 $\Rightarrow$ c = 16.

Vậy a = 30; b = 20; c = 16.

Câu 4:

a) Tìm chiều rộng và chiều dài của hình chữ nhật, biết chúng tỉ lệ với 3; 4 và hình chữ nhật có chu vi là 56 mét.

b) Một ô tô chạy từ A đến B với vận tốc 45km/h mất 3giờ. Hỏi ô tô chạy từ A đến B với vận tốc 65km/h mất bao nhiêu giờ? (kết quả làm tròn đến chữ số thập phân thứ nhất).

Xem đáp án

a) Gọi x, y lần lượt là chiều rộng và chiều dài hình chữ nhật (m) (y > x > 0).

Vì chiều rộng và chiều dài của hình chữ nhật tỉ lệ với 3 và 4 nên $\frac{x}{3} = \frac{y}{4}$ ;

Chu vi của hình chữ nhật là 56 mét nên 2(x + y) = 56.

Áp dụng tính chất dãy tỉ số bằng nhau, ta có:

$\frac{x}{3} = \frac{y}{4} = \frac{x + y}{3 + 4} = \frac{28}{7} = 4$ .

Do đó x = 3 . 4 = 12;

y = 4 . 4 = 16.

Vậy hình chữ nhật có chiều rộng là 12m và chiều dài là 16m.

b) Gọi x (giờ) là thời gian để ô tô chạy từ A đến B với vận tốc 65km/h.

Điều kiện: x > 0.

Hai ô tô cùng chạy trên một quãng đường AB nên vận tốc và thời gian của ô tô là hai đại lượng tỉ lệ nghịch.

Suy ra: $\frac{x}{3} = \frac{45}{65}$ .

Do đó $x = \frac{3 . 45}{65} = \frac{27}{13} \approx 2,1$ .

Vậy ô tô chạy từ A đến B với vận tốc 65km/h mất khoảng 2,1 giờ.

Câu 5:

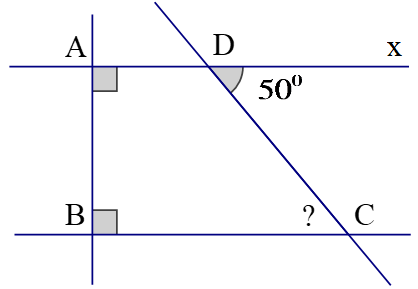
1) Cho hình vẽ. Tính số đo của $\hat{A C B}$ trong hình vẽ bên dưới.

2) Cho tam giác ABC vuông tại A có $\hat{B} = 60^{o}$ . Vẽ AHBC tại H.

a) Tính số đo góc HAB.

b) Trên cạnh AC lấy điểm D sao cho AD = AH. Gọi I là trung điểm của cạnh HD. Chứng minh ∆AHI = ∆ADI. Từ đó suy ra AI ^ HD.

c) Tia AI cắt cạnh HC tại điểm K. Chứng minh AB // KD.

Xem đáp án

1) Dựa vào hình vẽ, ta có: $A D ⊥ A B$ và $A B ⊥ B C$ .

Nên AD // BC (quan hệ giữa tính vuông góc với tính song song).

Vì AD // BC mà $\hat{C D x}$ và $\hat{A C B}$ là hai góc so le trong.

Nên $\hat{A C B}$ = $\hat{C D x}$ = 50^o.

Vậy $\hat{A C B}$ = 50^o.

2) Cho tam giác ABC vuông tại A có $\hat{B} = 60^{o}$ . Vẽ AH vuông góc BC tại H.

a) Tính số đo góc HAB.

Xét ∆AHB vuông tại H có:

$\hat{H B A} + \hat{H A B} = 90^{o}$ (hai góc phụ nhau)

$\Rightarrow \hat{H A B} = 90^{o} - \hat{H B A} = 90^{o} - 60^{o} = 30^{o}$

Vậy $\hat{H A B} = 30^{o}$ .

b) Chứng minh ∆AHI = ∆ADI. Từ đó suy ra AI ^ HD.

Xét DAHI và DADI có:

AH = AD (gt)

IH = ID (gt)

AI cạnh chung

Do đó DAHI = DADI (c.c.c)

Suy ra $\hat{H I A} = \hat{D I A}$ (hai góc tương ứng)

Mà $\hat{H I A} + \hat{D I A} = 180^{o}$ (hai góc kề bù)

Nên $\hat{H I A} = \hat{D I A} = 90^{o}$

Do đó $A I ⊥ H D$ (đpcm).

c) Chứng minh AB // KD.

DAHI = DADI (cmt)

$\Rightarrow \hat{H A K} = \hat{D A K}$ (hai góc tương ứng).

Xét DAHK và DADK có:

AH = AD (cmt)

$\hat{H A K} = \hat{D A K}$ (cmt)

Cạnh AK chung.

Do đó $Δ A H K = Δ A D K$ (c.g.c)

$\Rightarrow \hat{A D K} = \hat{A H K} = 90^{o}$ (hai góc tương ứng)

$\Rightarrow K D ⊥ A C$ .

Mà $A B ⊥ A C$ (gt).

Do đó KD //AB (đpcm).

Câu 6:

Tìm x biết: |3x −1| + |1 – 3x| = 6

Xem đáp án

Vì 3x – 1 và 1 – 3x là hai số đối nhau, nên: |3x −1| = |1 – 3x|

Suy ra: 2 |3x −1| = 6 hoặc |3x −1| = 3

- Trường hợp 1: 3x −1 = 3

3x = 3 + 1

3x = 4

$x = \frac{4}{3}$ .

- Trường hợp 2: 3x −1 = −3

3x = −3 + 1

3x = −2

$x = \frac{- 2}{3}$ .

Vậy $x \in {\frac{4}{3}; \frac{- 2}{3}}$ .