Trắc nghiệm Toán 7 CD Bài 12. Tính chất ba đường trung trực của tam giác (Phần 2) có đáp án
Trắc nghiệm Toán 7 CD Bài 12. Tính chất ba đường trung trực của tam giác (Vận dụng) có đáp án
-
653 lượt thi
-
3 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 1:
Cho tam giác ABC vuông tại A. Đường trung trực của AB cắt BC tại M. Gọi N là trung điểm của AC. Biết AB = 20 cm. Độ dài MN là
 Xem đáp án
Xem đáp án
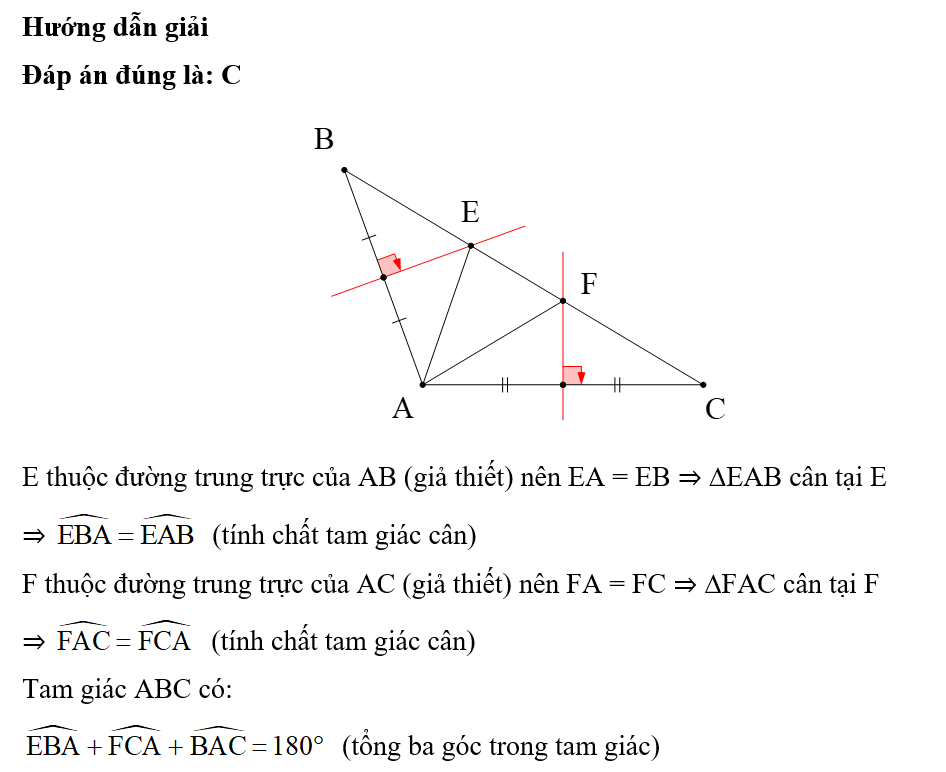
Hướng dẫn giải
Đáp án đúng là: B
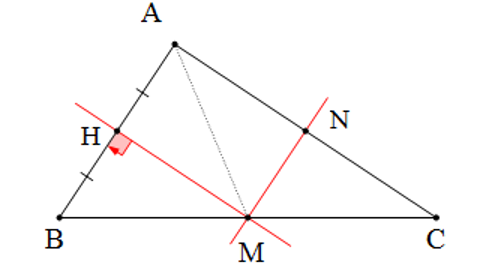
M thuộc đường trung trực của AB nên MA = MB (tính chất đường trung trực)
⇒ ∆MAB cân tại M ⇒ (tính chất)
Tam giác ABC vuông tại A nên:
Và
Do đó ⇒ ∆MAC cân tại M ⇒ MA = MC
Do đó M thuộc đường trung trực của AC
Lại có N là trung điểm của AC (giả thiết)
Suy ra MN là đường trung trực của AC
⇒ MN ⊥ AC
Mà AB ⊥ AC
Do đó MN // AB ⇒ (hai góc so le trong)
Gọi H là trung điểm của AC
Xét hai tam giác vuông AHM và MNA có
AM là cạnh chung
(cmt)
Suy ra ∆AHM = ∆MNA (cạnh huyền – góc nhọn)
Do đó AH = MN (hai cạnh tương ứng)
Mà AH =
Nên
Vậy MN = 10 cm.
Câu 3:
Cho ∆ABC có . M là điểm nằm giữa B và C. Vẽ điểm E sao cho AB là trung trực của ME, Điểm F sao cho AC là trung trực của MF. Khẳng định nào dưới đây sai?
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: D
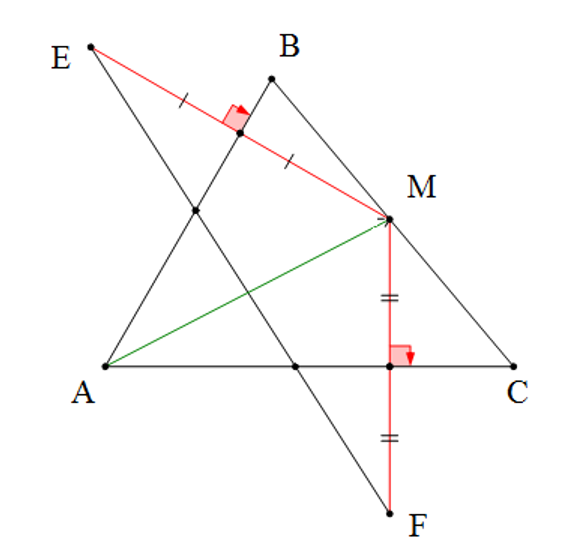
+) Ta có AB là trung trực của ME (giả thiết) ⇒ AE = AM (tính chất đường trung trực)
AC là trung trực của MF (giả thiết) ⇒ AF = AM (tính chất đường trung trực)
Do đó AE = AF ⇒ A thuộc đường trung trực của EF
Hay trung trực của EF đi qua A.
+) Ta có: B thuộc đường trung trực của ME ⇒ BE = BM (tính chất đường trung trực)
C thuộc đường trung trực của MF ⇒ CF = CM (tính chất đường trung trực)
Mà BM + CM = BC
Nên BE + CF = BC
+) Xét ∆AEB và ∆AMB có
AE = AM
AB là cạnh chung
EB = MB
Suy ra ∆AEB = ∆AMB (c.c.c)
⇒ (hai góc tương ứng)
Xét ∆AFC và ∆AMC có
AF = AM
AC là cạnh chung
FC = MC
Suy ra ∆AFC = ∆AMC (c.c.c)
⇒ (hai góc tương ứng)
Ta có:
⇒ .