Trắc nghiệm Toán 7 CTST Bài 6. Tính chất ba đường trung trực của tam giác có đáp án (Phần 2)
Trắc nghiệm Toán 7 CTST Bài 6. Tính chất ba đường trung trực của tam giác có đáp án (Phần 2) (Thông hiểu)
-
630 lượt thi
-
7 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 1:
Cho tam giác ABC có M là trung điểm của BC. Các đường trung trực của AB và AC cắt nhau tại O. Số đo góc OMC là:
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: A
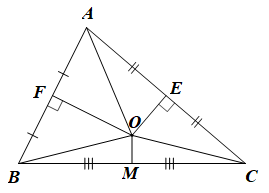
Do các đường trung trực của AB và AC cắt nhau tại O nên O là giao điểm của ba đường trung trực của tam giác ABC.
Do đó O nằm trên đường trung trực của BC.
Mà M là trung điểm của BC nên OM là trung trực của BC.
Suy ra OM vuông góc với BC nên \(\widehat {OMC} = 90^\circ \).
Vậy ta chọn phương án A.
Câu 2:
Cho góc xOy có số đo là 50º, điểm A nằm trong góc xOy. Vẽ điểm M sao cho Ox là trung trực của AM, vẽ điểm N sao cho Oy là trung trực của AN. Số đo góc MON là:
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: C
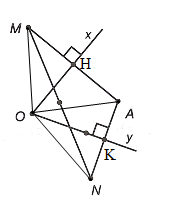
Xét tam giác AMN có O là giao điểm hai đường trung trực của AM và AN nên O cách đều ba đỉnh A, M, N hay OA = OM = ON.
Gọi H là giao điểm của Ox và MA, K là giao điểm của Oy và AN.
Xét ΔAOH và ΔMOH có
\(\widehat {OHA} = \widehat {OHM} = 90^\circ \),
OA = OM (chứng minh trên),
OH là cạnh chung
Do đó ΔAOH = ΔMOH (cạnh huyền – cạnh góc vuông).
Suy ra \(\widehat {AOH} = \widehat {MOH}\)(hai góc tương ứng)
Chứng minh tương tự ta cũng có:
ΔAOK = ΔNOK (cạnh huyền – cạnh góc vuông).
Suy ra \(\widehat {AOK} = \widehat {NOK}\)(hai góc tương ứng)
Ta có \(\widehat {MON} = \widehat {MOH} + \widehat {AOH} + \widehat {AOK} + \widehat {KON}\)
Mà \(\widehat {AOH} = \widehat {MOH}\), \(\widehat {AOK} = \widehat {NOK}\) (chứng minh trên).
Suy ra \(\widehat {MON} = 2\widehat {AOH} + 2\widehat {AOK}\)
Hay \(\widehat {MON} = 2(\widehat {AOH} + \widehat {AOK}) = 2\widehat {xOy} = 2.50^\circ = 100^\circ \).
Vậy ta chọn phương án C.
Câu 3:
Cho góc nhọn \(\widehat {xOy}\), trên tia Ox lấy điểm A, trên tia Oy lấy điểm B sao cho OA = OB. Đường trung trực của OA và đường trung trực của OB cắt nhau tại I.
Cho các khẳng định sau:
(I) OI là tia phân giác của \(\widehat {xOy}\);
(II) OI là đường trung trực của đoạn AB.
Chọn khẳng định đúng:
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: C
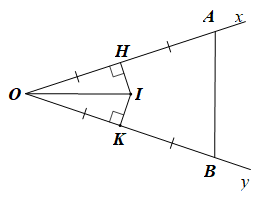
Vì HI là trung trực của OA nên IH ⊥ OA, OH = HA = \(\frac{1}{2}\)OA;
Vì KI là trung trực của OB nên IK ⊥ OB, OK = KB = \(\frac{1}{2}\)OB.
Mà OA = OB (giả thiết) nên OH = OK.
Xét DOIH và DOIK có
\(\widehat {OHI} = \widehat {OKI}( = 90^\circ )\),
OI là cạnh chung,
OH = OK (chứng minh trên)
Do đó DOIH = DOIK (cạnh huyển – cạnh góc vuông).
Suy ra \(\widehat {HOI} = \widehat {KOI}\) (hai góc tương ứng).
Do đó OI là tia phân giác của \(\widehat {xOy}\), nên (I) đúng.
Xét DOAB có IH là trung trực của OA, IK là trung trực của OB, IH cắt IK tại H nên I là giao điểm của ba đường trung trực trong tam giác OAB.
Do đó OI là trung trực của AB, nên (II) đúng.
Vậy ta chọn phương án C.
Câu 4:
Cho tam giác ABC có AB < AC. Trên AC lấy điểm D sao cho AB = CD. O là giao điểm của các đường trung trực của BD và AC. Phát biểu nào sau đây là đúng?
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: B
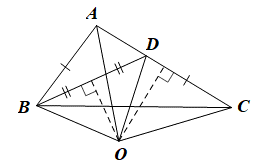
Vì O thuộc đường trung trực của AC nên OA = OC;
Vì O thuộc đường trung trực của BD nên OB = OD.
Xét ΔAOB và ΔCOD có
OA = OC (chứng minh trên),
OB = OD (chứng minh trên),
AB = CD (giả thiết)
Do đó ΔAOB = ΔCOD (c.c.c).
Vậy ta chọn phương án B.
Câu 5:
Cho tam giác ABC có AB < AC. Trên AC lấy điểm D sao cho AB = CD. O là giao điểm của các đường trung trực của BD và AC. Phát biểu nào sau đây là đúng?
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: B
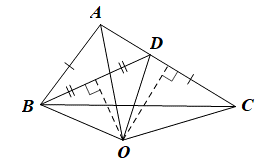
Vì O thuộc đường trung trực của AC nên OA = OC;
Vì O thuộc đường trung trực của BD nên OB = OD.
Xét ΔAOB và ΔCOD có
OA = OC (chứng minh trên),
OB = OD (chứng minh trên),
AB = CD (giả thiết)
Do đó ΔAOB = ΔCOD (c.c.c).
Suy ra \(\widehat {OAB} = \widehat {OCD}\) (hai góc tương ứng) (1)
Mặt khác OA = OC nên tam giác OAC cân tại O
Suy ra \(\widehat {OAC} = \widehat {OCA}\) hay \(\widehat {OAC} = \widehat {OCD}\) (2)
Từ (1) và (2) ta có \(\widehat {OAB} = \widehat {OAC}\) nên AO là tia phân giác của góc BAC.
Vậy ta chọn phương án B.
Câu 6:
Cho tam giác ABC có góc A là góc tù. Gọi M, N lần lượt là trung điểm của AB và AC. Vẽ đường trung trực của các cạnh AB, AC cắt BC lần lượt tại D và E. Biết BD = 3 cm, DE = 2 cm, EC = 4 cm. Chu vi tam giác ADE bằng:
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: D
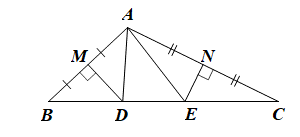
Vì DM là đường trung trực của cạnh AB nên DA = DB = 3 cm.
Vì EN là đường trung trực của cạnh AC nên EA = EC = 4 cm.
Chu vi tam giác ADE là:
AD + DE + AE = 3 + 2 + 4 = 9 (cm).
Vậy ta chọn phương án D.
Câu 7:
Cho tam giác ABC nhọn, đường cao AH. Lấy điểm D sao cho AB là trung trực của HD. Lấy điểm E sao cho AC là trung trực của HE. Gọi M là giao điểm của DE và AB, gọi N là giao điểm của DE và AC. Khẳng định nào sau đây là đúng?
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: C
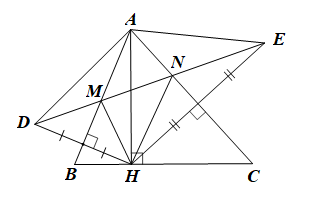
Xét DDHE có AB, AC là hai đường trung trực của tam giác cắt nhau tại A nên A cách đều ba đỉnh của tam giác
Do đó AD = AH = AE.
Tam giác ADE có AD = AE nên là tam giác cân tại A.
Suy ra \(\widehat {ADE} = \widehat {AED}\) (tính chất tam giác cân) (1)
Xét DADM và DAHM có
AM là cạnh chung,
DM = HM (do M thuộc trung trực của DH),
AD = AH (chứng minh trên).
Do đó DADM = DAHM (c.c.c).
Suy ra \(\widehat {ADM} = \widehat {AHM}\)(hai góc tương ứng) (2)
Xét DANH và DANE có
AN là cạnh chung,
NH = NE (do N thuộc trung trực của EH),
AH = AE (chứng minh trên)
Do đó DANH = DANE (c.c.c)
Suy ra \(\widehat {AHN} = \widehat {AEN}\)(hai góc tương ứng) (3)
Từ (1), (2) và (3) suy ra \(\widehat {AHN} = \widehat {AHM}\)
Do đó HA là tia phân giác của góc MHN.
Vậy ta chọn phương án C.
