Trắc nghiệm Toán 7 CTST Bài 6. Tính chất ba đường trung trực của tam giác có đáp án (Phần 2)
Trắc nghiệm Toán 7 CTST Bài 6. Tính chất ba đường trung trực của tam giác có đáp án (Phần 2) (Vận dụng)
-
631 lượt thi
-
3 câu hỏi
-
30 phút
Danh sách câu hỏi
Câu 1:
Cho tam giác ABC nhọn. Các đường trung trực của AB và AC cắt nhau tại O. Trên tia đối của tia OB lấy điểm D sao cho OB = OD. Biết \(\widehat {ABC} = 75^\circ \), số đó góc ADC là:
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: C
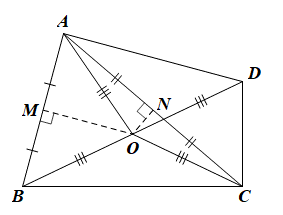
Xét DABC có O là giao điểm của hai đường trung trực của tam giác nên O cách đều ba đỉnh A, B, C.
Do đó OA = OB = OC.
• Tam giác ABO có OA = OB nên DABO cân tại O.
Suy ra \(\widehat {OAB} = \widehat {OBA}\) hay \(\widehat {OAB} = \widehat {DBA}\).
• Ta có OA = OC (chứng minh trên) và OB = OD (giả thiết)
Suy ra OA = OD nên tam giác OAD cân tại O.
Do đó \(\widehat {OAD} = \widehat {ODA}\)hay \(\widehat {OAD} = \widehat {BDA}\).
• Xét DABD có \(\widehat {DAB} + \widehat {BDA} + \widehat {DBA} = 180^\circ \) (tổng ba góc trong một tam giác)
Hay \(\widehat {OAB} + \widehat {OA{\rm{D}}} + \widehat {BDA} + \widehat {DBA} = 180^\circ \)
Mà \(\widehat {OAB} = \widehat {DBA}\), \(\widehat {OAD} = \widehat {BDA}\) (chứng minh trên)
Suy ra \(2(\widehat {BDA} + \widehat {DBA}) = 180^\circ \)
Do đó \(\widehat {BDA} = 90^\circ - \widehat {DBA}\) (1)
Chứng minh tương tự ta cũng có \(\widehat {BDC} = 90^\circ - \widehat {DBC}\) (2)
Từ (1) và (2) suy ra \(\widehat {BDA} + \widehat {BDC} = 180^\circ - (\widehat {DBA} + \widehat {DBC})\)
Hay \(\widehat {ADC} = \widehat {BDA} + \widehat {BDC} = 180^\circ - \widehat {CBA} = 180^\circ - 75^\circ = 105^\circ \).
Do đó \(\widehat {ADC} = 105^\circ \)
Vậy ta chọn phương án C.
Câu 2:
Cho ΔABC có góc A bằng 100°. Các đường trung trực của AB và AC cắt cạnh BC theo thứ tự tại E và F. Số đo góc EAF là:
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: A
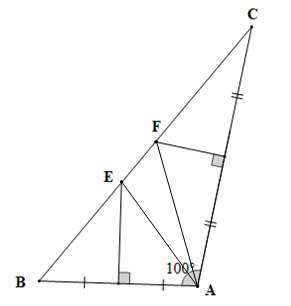
Vì E thuộc đường trung trực của AB nên EA = EB
Do đó tam giác ABE cân tại E
Suy ra \(\widehat B = \widehat {{\rm{BAE}}}\)
Vì F thuộc đường trung trực của AC nên FA = FC
Do đó tam giác ACF cân tại F
Suy ra \(\widehat C = \widehat {{\rm{FAC}}}\)
Xét DABC có \(\widehat B + \widehat {{\rm{CAB}}} + \widehat C = 180^\circ \) (tổng ba góc trong một tam giác)
Suy ra \(\widehat B + \widehat C = 180^\circ - \widehat {{\rm{CAB}}} = 180^\circ - 100^\circ = 80^\circ \)
Ta có \(\widehat {{\rm{CAB}}} = \widehat {BA{\rm{E}}} + \widehat {EAF} + \widehat {FAC}\)
Mà \(\widehat B = \widehat {{\rm{BAE}}}\),\(\widehat C = \widehat {{\rm{FAC}}}\),\(\widehat {CAB} = 100^\circ \)
Suy ra \(\widehat {FA{\rm{E}}} = \widehat {{\rm{CAB}}} - \widehat B - \widehat C = 100^\circ - 80^\circ = 20^\circ \).
Vậy ta chọn phương án A.
Câu 3:
Cho tam giác ABC có \(\widehat A = \alpha \) là góc tù. Các đường trung trực của các cạnh AB và AC cắt nhau tại I. Tính số đo của góc BIC theo α ta được:
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: C
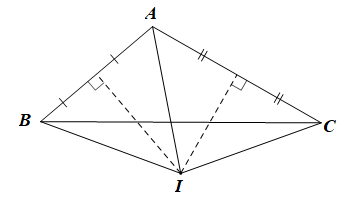
Xét DABC có I là giao điểm của hai đường trung trực của AB và AC nên I cách đều ba đỉnh của tam giác.
Do đó IA = IB = IC.
• Tam giác IAB có IA = IB nên cân tại I
Suy ra \[\widehat {IAB} = \widehat {IBA}\] (tính chất tam giác cân).
• Tam giác IAC có IA = IC nên cân tại I
Suy ra \[\widehat {IAC} = \widehat {ICA}\] (tính chất tam giác cân).
Xét DABI có \[\widehat {IAB} + \widehat {IBA} + \widehat {AIB} = 180^\circ \] (tổng ba góc trong một tam giác)
Mà \[\widehat {IAB} = \widehat {IBA}\](chứng minh trên)
Suy ra \[\widehat {AIB} = 180^\circ - 2.\widehat {IAB}\]
Xét DACI có \[\widehat {IAC} + \widehat {ICA} + \widehat {AIC} = 180^\circ \] (tổng ba góc trong một tam giác)
Mà \[\widehat {IAC} = \widehat {ICA}\] (chứng minh trên)
Suy ra \[\widehat {AIC} = 180^\circ - 2.\widehat {IAC}\]
Ta có \(\widehat {BIC} = \widehat {AIB} + \widehat {AIC} = 180^\circ - 2.\widehat {IAB} + 180^\circ - 2.\widehat {IAC}\)
Hay \(\widehat {BIC} = 360^\circ - 2.(\widehat {IAB} + .\widehat {IAC}) = 360^\circ - 2.\widehat {BAC} = 360^\circ - 2\alpha \).
Vậy ta chọn phương án C.
