Trắc nghiệm Toán 7 Bài 35. Sự đồng quy của ba đường trung trực, ba đường cao trong một tam giác có đáp án
Dạng 2. Xác định trực tâm của tam giác
-
295 lượt thi
-
10 câu hỏi
-
45 phút
Danh sách câu hỏi
Câu 1:
Giao của ba đường cao trong một tam giác có tên gọi là gì?
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: A
Giao của ba đường cao trong một tam giác có gọi là trực tâm của tam giác.
Câu 2:
Hãy chọn khẳng định đúng trong các khẳng định sau:
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: D
Khẳng định A chỉ đúng với tam giác tù;
Khẳng định B chỉ đúng với tam giác nhọn;
Khẳng định C chỉ đúng với tam giác vuông.
Vậy chọn phương án D.
Câu 3:
Cho ∆ABC vuông tại B. Điểm nào là trực tâm của ∆ABC?
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: A
Vì ∆ABC vuông tại B.
Suy ra AB ⊥ BC nên AB là đường cao; CB ⊥ BA nên CB là đường cao.
Do đó B là giao điểm của các đường cao kẻ từ A và từ C.
Vậy B là trực tâm của ∆ABC.
Câu 4:
Cho hình vẽ
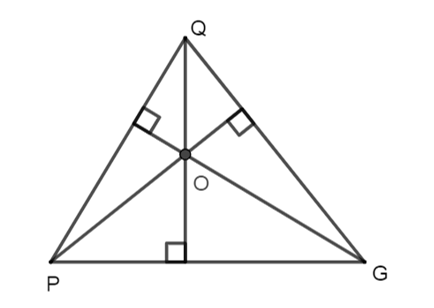
Các đường cao của ∆PQG cắt nhau tại O thì
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: B
Ba đường cao của một tam giác đồng quy tại một điểm. Điểm đồng quy của ba đường cao của một tam giác gọi là trực tâm của tam giác đó.
Câu 5:
Cho ∆ABC cân tại A, đường trung tuyến AD và đường cao BK cắt nhau tại E. Khẳng định nào dưới đây là đúng?
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là:D
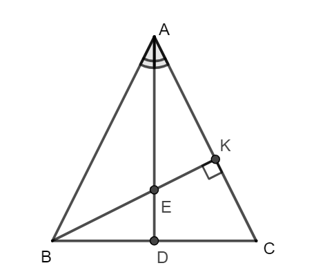
Vì ∆ABC cân tại A nên AD ⊥ BC hay AD là đường cao của ∆ABC.
Mà BK ⊥ AC nên BK là đường cao của ∆ABC.
Xét ∆ABC có hai đường cao AD, BK cắt nhau tại E nên E là trực tâm của ∆ABC.
Suy ra CE ⊥ AB.
Vậy cả A, B, C đều đúng. Ta chọn phương án D.
Câu 6:
Trên đường thẳng d có ba điểm phân biệt I, J, K (J ở giữa I và K). Lấy điểm M nằm ngoài đường thẳng d sao cho MJ vuông góc với d tại J. Đường thẳng qua I vuông góc với MK cắt MJ tại N. Điểm nào là trực tâm của tam giác MIK?
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: B
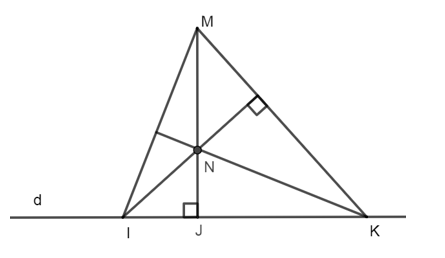
Ta có: MJ ⊥ IK tại J nên MJ là đường cao của ∆MIK.
Mà N nằm trên đường thẳng qua I và vuông góc với MK nên IN ⟘ MK.
Do đó IN là đường cao của ΔMIK.
Xét ∆MIK có hai đường cao IN và MJ cắt nhau tại N nên N là trực tâm của ΔMIK.
Câu 8:
Quan sát hình vẽ dưới đây.
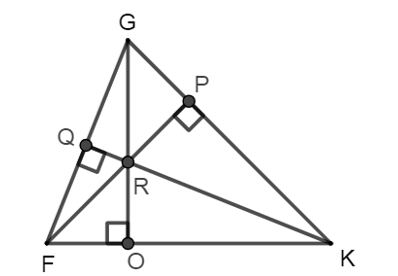
Khẳng định nào dưới đây là sai?
Xem đáp án
Hướng dẫn giải:
Đáp án đúng là: B
∆FRK có RG ⊥ FK, KG ⊥ FR và RG cắt KG tại G nên G là trực tâm của ∆FRK.
∆FPK vuông tại P nên trực tâm của ∆FPK là P.
∆GFK có GO ⊥ FK, FP ⊥ GK và GO cắt FP tại R nên R là trực tâm của ∆GFK.
Vậy ta chọn phương án B.
Câu 9:
Cho ∆ABC vuông tại A. Trên cạnh AC lấy điểm M bất kì (M ≠ A, C). Qua M kẻ đường thẳng vuông góc với BC tại N. Từ C kẻ đường thẳng vuông góc với BM tại P. Gọi D là giao điểm của AB và CP. Khẳng định nào sau đây sai?
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: D
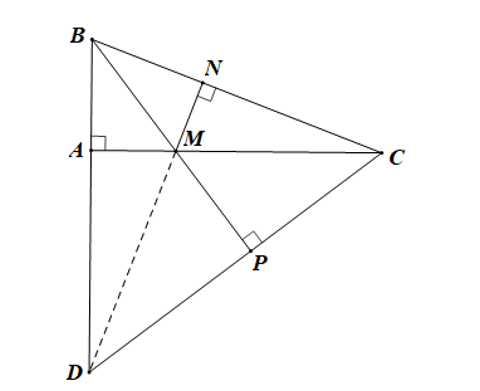
• Xét ∆DBC có CA, BP là hai đường cao cắt nhau tại M nên M là trực tâm của ∆DBC.
Do đó phương án A đúng.
• Vì M là trực tâm của ∆DBC nên DM ⊥ BC. Do đó phương án B đúng.
• Ta có DM ⊥ BC (chứng minh trên).
Mà MN ⊥ BC (giả thiết).
Suy ra D, M, N thẳng hàng.
Do đó phương án C đúng.
• Ta có:
+) D ∈ MN (do D, M, N thẳng hàng);
+) D ∈ AB (giả thiết);
+) D ∈ CP (giả thiết).
Suy ra AB, MN, CP cùng đồng quy tại điểm D.
Do đó phương án D sai.
Vậy ta chọn phương án D.
Câu 10:
Cho tam giác ABC vuông tại A, trên tia BA lấy M sao cho BM = BC. Tia phân giác góc B cắt AC tại H. Khẳng định nào sau đây là sai?
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: D
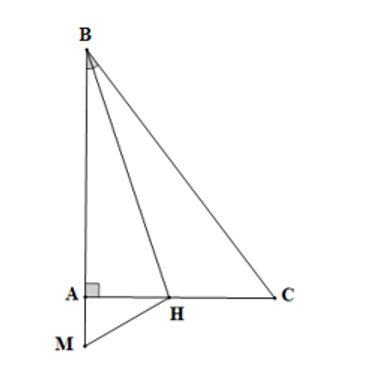
• Xét ΔBHM và ∆BHC có:
BH là cạnh chung,
(do BH là tia phân giác của góc ABC),
BM = BC (giả thiết)
Do đó ΔBHM = ∆BHC (c.g.c)
Suy ra MH = HC (hai cạnh tương ứng), nên C là khẳng định đúng.
• Vì BM = BC và HM = HC nên BH là đường trung trực của MC.
Do đó BH ⊥ MC hay BH là đường cao của tam giác MBC.
• Xét DBMC có hai đường cao BH và CA cắt nhau tại H nên H là trực tâm tam giác BMC. (Khẳng định B là đúng)
Do đó MH ⊥ BC nên khẳng định A là đúng.
Vậy ta chọn phương án D.