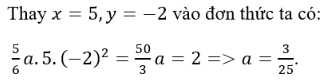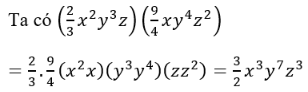14 câu hỏi trắc nghiệm thuộc Đề kiểm tra 1 tiết Toán 7 Chương 4 Đại Số có đáp án (Trắc nghiệm - Tự luận 2)

Đề kiểm tra 1 tiết Toán 7 Chương 4 Đại số có đáp án

Đề kiểm tra 1 tiết Toán 7 Chương 4 Đại Số có đáp án (Trắc nghiệm - Tự luận 2)

3602 lượt thi
14 câu hỏi
50 phút

BẮT ĐẦU LÀM BÀI

Danh sách câu hỏi

Câu 1:

A. Phần trắc nghiệm (4 điểm)

Trong mỗi câu dưới đây, hãy chọn phương án trả lời đúng:

Phần biến của đơn thức $5 x^{2} y (- 3 / 4 x y^{3} z) (- 3 z)$ là:

A. $- \frac{45}{4} x^{3} y^{2} z^{3}$

B. $\frac{45}{4} x^{3} y^{4} z^{2}$

C. $- \frac{45}{4} x^{3} y^{4} z^{2}$

D. $\frac{45}{4} x^{2} y^{3} z^{2}$

Xem đáp án

Chọn B

Câu 2:

Giá trị của đa thức $5 / 6 a x y^{2}$ (a là hằng số) tại $x = 5, y = - 2$ là 2. Tìm a.

A. $a = \frac{6}{25}$

B. $a = \frac{4}{25}$

C. $a = \frac{3}{25}$

D. $a = \frac{25}{3}$

Xem đáp án

Chọn C

Câu 3:

Tích của hai đơn thức $\frac{2}{3} x^{2} y^{3} z v à \frac{9}{4} x y^{4} z^{2}$ là:

A. $\frac{3}{2} x^{3} y^{7} z^{2}$

B. $\frac{3}{2} x^{7} y^{2} z^{3}$

C. $\frac{2}{3} x^{3} y^{7} z^{3}$

D. $\frac{3}{2} x^{3} y^{7} z^{3}$

Xem đáp án

Chọn D

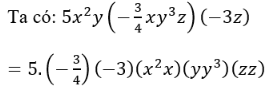
Câu 4:

Đa thức thu gọn của đa thức $2 x^{5} y^{2} - 3 x^{3} y + 8 + 9 x y - 2 x^{5} y^{2} + 4 x^{3} y - 4 x y - 7$ là:

A. $x^{3} y - 5 x y$

B. $x^{3} y + 5 x y + 15$

C. $x^{5} y^{2} + x^{3} y + 5 x y + 1$

D. $x^{3} y + 5 x y + 1$

Xem đáp án

Ta có: 2x5y2 - 3x3y + 8 + 9xy - 2x5y2 + 4x3y - 4xy - 7 = x3y + 5xy + 1. Chọn D

Câu 5:

Biết $C + (2 x^{2} y^{2} - 2 x y) = 4 x^{2} y^{2} + 6 x y + 9 y - 4 x + 5$ . Tìm C.

A. $2 x^{2} y^{2} + 8 x y + 9 y - 4 x + 5$

B. $6 x^{2} y^{2} + 8 x y - 9 y - 4 x + 5$

C. $2 x^{2} y^{2} + 4 x y - 9 y + 4 x + 5$

D. $6 x^{2} y^{2} + 4 x y + 9 y - 4 x + 5$

Xem đáp án

Ta có: C = (4x2y2 + 6xy + 9y - 4x + 5) - (2x2y2 - 2xy)

= 4x2y2+ 6xy + 9y - 4x + 5 - 2x2y2 + 2xy = 2x2y2 + 8xy + 9y - 4x + 5.

Chọn A

Câu 6:

Hệ số của $x^{4}$ trong đa thức $Q (x) = 5 x^{4} - x^{5} - x^{2} - 2 x^{3} + 3 x^{2} + 3 x - 2 x^{4} + 5$ là:

A. 2

B. 3

C. 5

D. 1

Xem đáp án

Thu gọn Q(x) = 5x4 - x5 - x2 - 2x3 + 3x2 + 3x - 2x4 + 5

= -x5 + 3x4 - 2x3 + 2x2 + 3x + 5

Hệ số của x4là 3. Chọn B

Câu 7:

Biết đa thức $f (x) = 5 / 4 x a + a + 1$ nhận x = -4 làm nghiệm. Tìm a.

A. $a = \frac{5}{4}$

B. $a = \frac{- 1}{4}$

C. $a = \frac{1}{4}$

D. $a = \frac{- 5}{4}$

Xem đáp án

Thay x=-4 vào f(x) ta có

5/4.(-4)a + a + 1 = 0 ⇒ -5a + a + 1 = 0

⇒ -4a + 1 = 0 ⇒ a = 1/4. Chọn C

Câu 8:

Nghiệm của đa thức $3 x^{2} - 12$ là:

A. x = 2, x = -2

B. x = 2

C. x = -2

D. Đa thức vô nghiệm

Xem đáp án

Ta có 3x2 - 12 = 0 ⇒ 3x2 = 12 ⇒ x2 = 4 ⇒ x = ±2. Chọn A

Câu 9:

B. Phần tự luận (6 điểm)

Cho hai đa thức

$f (x) = x^{3} - 3 x^{2} + 2 x - 5 + x^{2}, g (x) = - x^{3} - 5 x + 3 x^{2} + 3 x + 4 .$

a. Thu gọn các đa thức trên và sắp xếp theo lũy thừa giảm dần của biến.

Xác định bậc của mỗi đa thức

Xem đáp án

a. Ta có:

f(x) = x3 - 3x2 + 2x - 5 + x2 = x3 -2x2 + 2x- 5

Bậc của đa thức f(x) là 3 (0.5 điểm)

g(x) = -x3 - 5x + 3x2 + 3x + 4 = -x3 + 3x2 - 2x + 4

Bậc của đa thức g(x) là 3 (0.5 điểm)

Câu 10:

Cho hai đa thức

$f (x) = x^{3} - 3 x^{2} + 2 x - 5 + x^{2}, g (x) = - x^{3} - 5 x + 3 x^{2} + 3 x + 4 .$

b. Tính f(x) + 2g(x) và 2f(x) - g(x)

Xem đáp án

b. Ta có f(x) + 2g(x)

= x3 - 2x2 + 2x- 5 + 2(-x3 + 3x2 - 2x + 4)

= x3 - 2x2 + 2x - 5 + (-2x3) + 6x2 - 4x + 8

=-x3 + 4x2 - 2x + 3 (0.5 điểm)

2f(x) - g(x) = x3 - 2x2 + 2x- 5 - 2(-x3+ 3x2 - 2x + 4)

= x3 - 2x2 + 2x - 5 + 2x3 - 6x2 + 4x - 8

= 3x3 - 8x2 + 6x - 13 (0.5 điểm)

Câu 11:

Cho hai đa thức

$f (x) = x^{3} - 3 x^{2} + 2 x - 5 + x^{2}, g (x) = - x^{3} - 5 x + 3 x^{2} + 3 x + 4 .$

c. Tính nghiệm của f(x) + g(x)

Xem đáp án

c. Ta có f(x) + g(x)

=(x3 - 2x2 + 2x - 5) + (-x3 + 3x2 - 2x + 4) = x2 - 1

Ta có x2 - 1 = 0 ⇒ x2 = 1 ⇒ x = 1,x = -1

Vậy nghiệm của đa thức h(x) là x = ±1 (1 điểm)

Câu 12:

Cho hai đơn thức $A = (3 x^{4} y^{5}) (- 2 x^{3} y^{5}) v à B = {(- 3 x y^{2})}^{2} {(- 2 x^{2} y^{3})}^{2} .$

a. Hãy thu gọn các đơn thức trên

Xem đáp án

a. A = (3x4y5) (-2x3y5) = 3.(-2) (x4x3) (y5y5) = -6x7y10 (0.5 điểm)

B = (-3xy2)2(-2x2y3)2= 9x2y4.4x4y6= 36x6y10 (0.5 điểm)

Câu 13:

Cho hai đơn thức $A = (3 x^{4} y^{5}) (- 2 x^{3} y^{5}) v à B = {(- 3 x y^{2})}^{2} {(- 2 x^{2} y^{3})}^{2} .$

b. Cho biết bậc và chỉ rõ phần biến, phần hệ số của mỗi đơn thức

Xem đáp án

b. Bậc của A là 17, phần hệ số là -6, phần biến là x7y10 (0.5 điểm)

Bậc của B là 16, phần hệ số là 36, phần biến là x6y10 (0.5 điểm)

Câu 14:

Cho đa thức $F (x) = 2 a x^{2} + b x$ (a,b là hằng số). Xác định a,b để đa thức F(x) có nghiệm $x = - 1 v à F (1) = 4$

Xem đáp án

Cho đa thức F(x) = 2ax2 + bx (a,b là hằng số). Xác định a,b để đa thức F(x) có nghiệm x = -1 và F(1) = 4

Vì đa thức F(x) có nghiệm x = -1 nên thay F(-1) = 0

⇒ 2a - b = 0 ⇒ b = 2a (0.5 điểm)

Vì F(1) = 4 ⇒ 2a + b = 4 ⇒ b = 4 - 2a

Từ đây ta có 2a = 4 - 2a ⇒ 4a = 4 ⇒ a = 1 (0.5 điểm)

Bắt đầu thi ngay