25 câu hỏi trắc nghiệm thuộc Trắc nghiệm Toán 12 Bài Khái niệm về khối đa diện có đáp án (Mới nhất)

Câu 1:

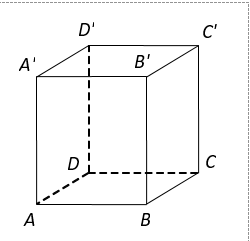
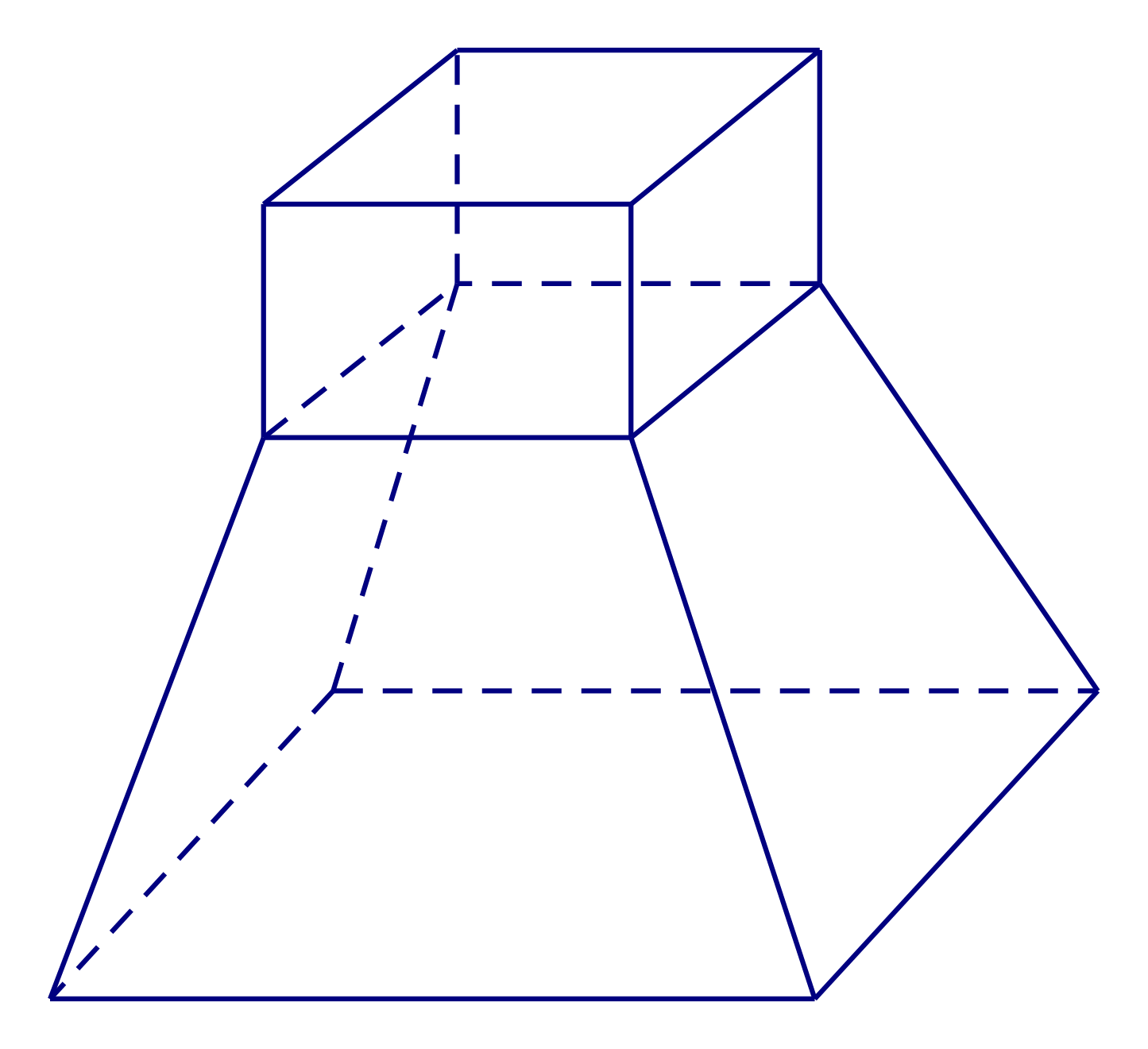
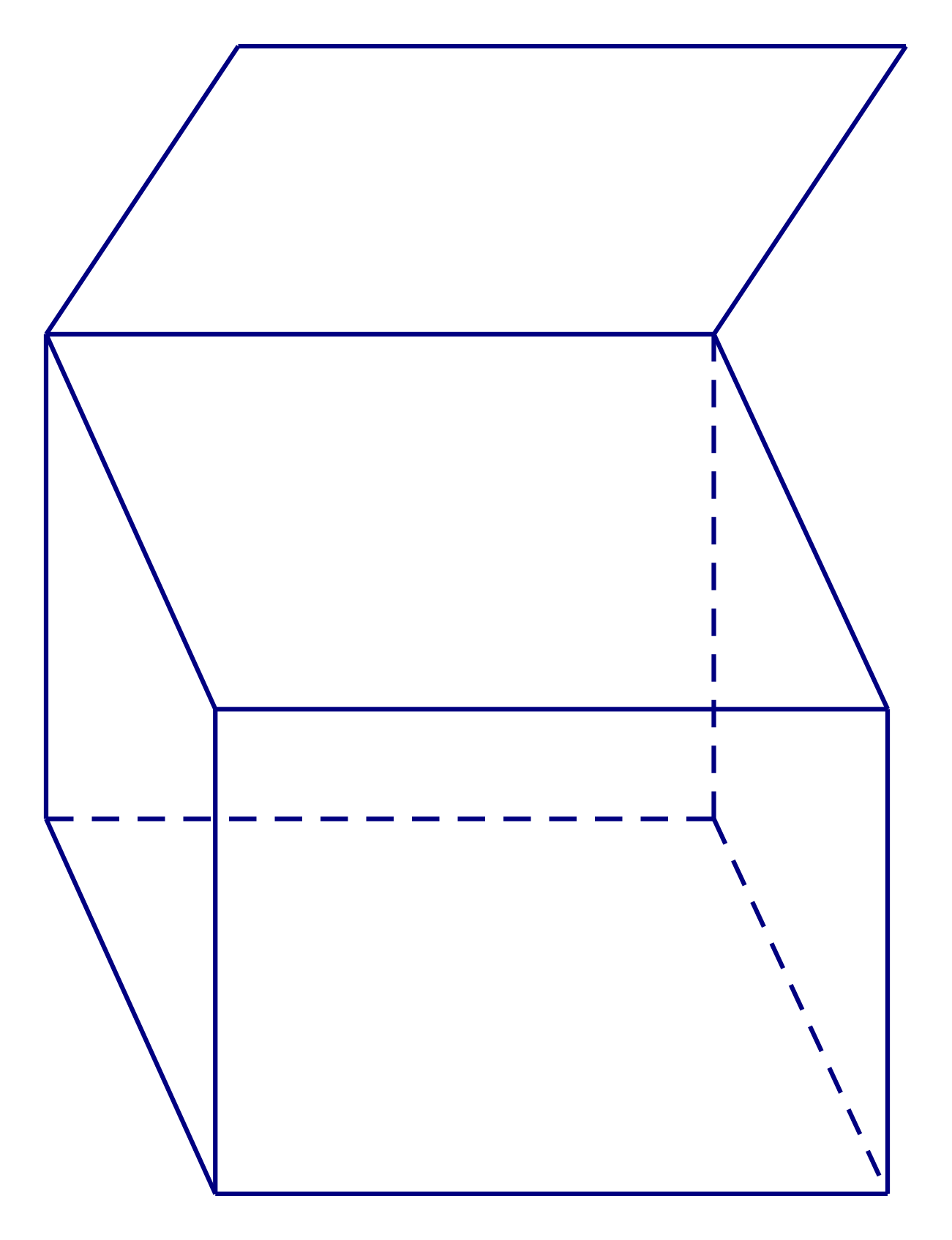
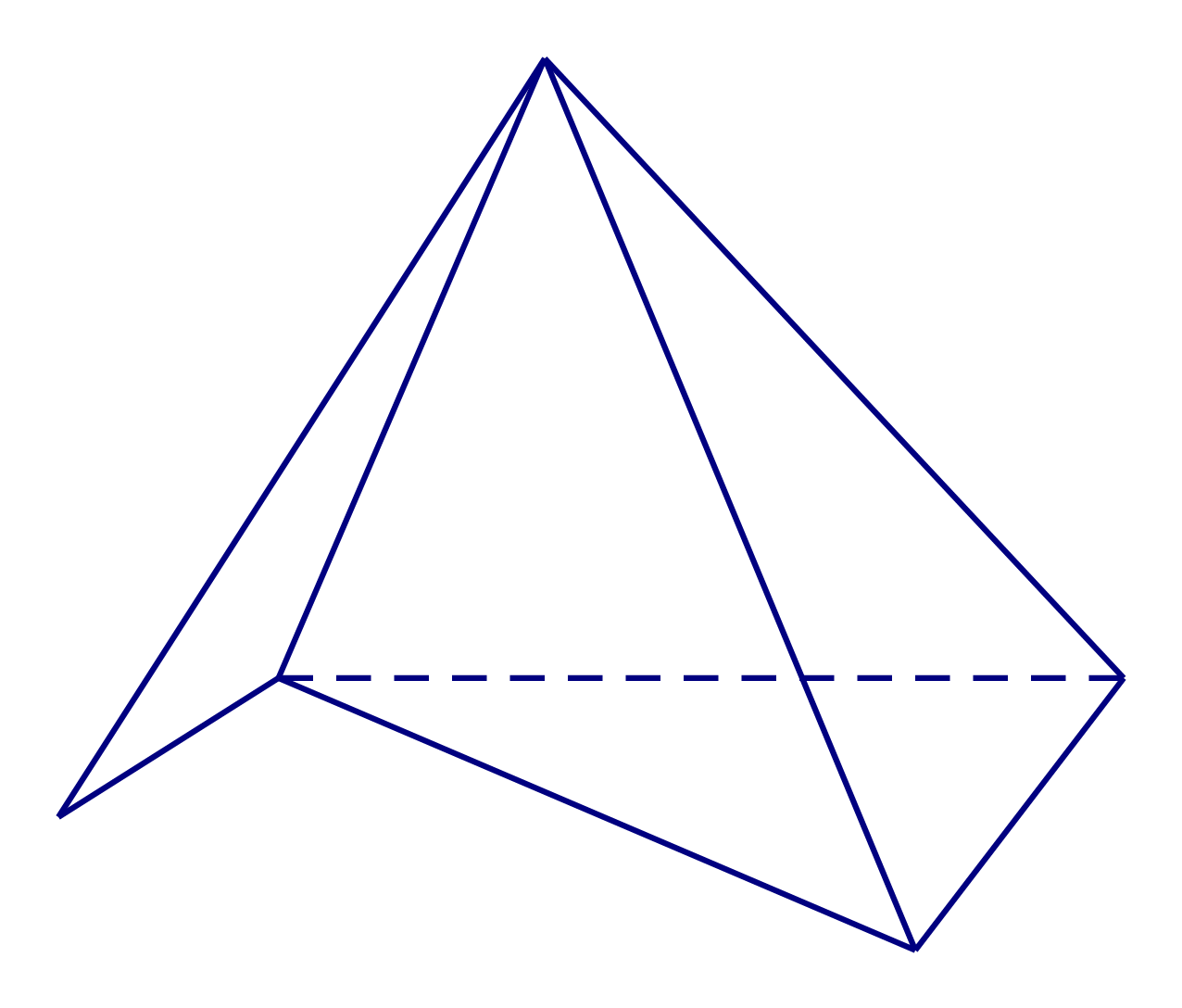
Cho các hình sau:


Hình 1	Hình 2	Hình 3	Hình 4

Mỗi hình trên gồm một số hữu hạn đa giác phẳng (kể cả các điểm trong của nó), hình đa diện là:

A. Hình 1.

B. Hình 2.

C. Hình 3.

D. Hình 4.

Xem đáp án

Chọn A.

Câu 2:

Cho các hình sau:


Hình 1	Hình 2	Hình 3	Hình 4

Mỗi hình trên gồm một số hữu hạn đa giác phẳng (kể cả các điểm trong của nó), hình không phải đa diện là:

A. Hình 1.

B. Hình 2.

C. Hình 3.

D. Hình 4.

Xem đáp án

Chọn D.

Câu 3:

Cho các hình sau:

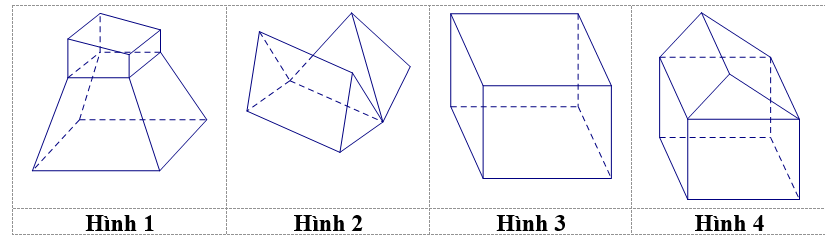
Media VietJack

Mỗi hình trên gồm một số hữu hạn đa giác phẳng (kể cả các điểm trong của nó), số hình đa diện là:

A. 1

B. 2.

C. 3.

D. 4.

Xem đáp án

Các hình đa diện là: Hình 1; Hình 3; Hình 4. Chọn C.

Câu 4:

Vật thể nào trong các vật thể sau không phải là khối đa diện?

A.

B.

C.

D.

Xem đáp án

Chọn C. Vì hình C vi phạm tính chất Mỗi cạnh của miền đa giác nào cũng là cạnh chung của đúng hai miền đa giác.

Câu 5:

Hình đa diện trong hình vẽ bên có bao nhiêu mặt ?

A. 6

B.10

C. 11

D. 12

Xem đáp án

Chọn C.

Câu 6:

Hình đa diện trong hình vẽ bên có bao nhiêu mặt ?

A. 8

B. 10

C. 11

D. 12

Xem đáp án

Chọn B.

Câu 7:

Hình đa diện trong hình vẽ bên có bao nhiêu mặt ?

A. 11

B. 12

C. 13

D. 14

Xem đáp án

Chọn B.

Câu 8:

Khối đa diện nào sau đây có số mặt nhỏ nhất?

Media VietJack

A. Khối tứ diện đều.

Media VietJack

B. Khối chóp tứ giác.

Media VietJack

C. Khối lập phương

Media VietJack

D. Khối 12 mặt đều.

Xem đáp án

Chọn A.

Câu 9:

Hình đa diện trong hình vẽ bên có bao nhiêu cạnh?

A. 8

B. 9

C. 12

D. 16

Xem đáp án

Chọn D.

Câu 10:

Cho một hình đa diện. Trong các khẳng định sau, khẳng định nào sai?

A. Mỗi đỉnh là đỉnh chung của ít nhất ba cạnh.

B. Mỗi mặt có ít nhất ba cạnh.

C. Mỗi cạnh là cạnh chung của ít nhất ba mặt.

D. Mỗi đỉnh là đỉnh chung của ít nhất ba mặt.

Xem đáp án

Ta thấy các đáp án A, B, D đều đúng dựa vào khái niệm hình đa diện.

Chọn C.

Câu 11:

Gọi Đ là số các đỉnh, là số các mặt, là số các cạnh của một hình đa diện bất kỳ. mệnh đề nào sau đây là đúng?

A. $Đ > 4, M > 4, C > 6.$

B.

Đ > 5, M > 5, C > 7.

C.

Đ \geq 4, M \geq 4, C \geq 6.

D. $Đ \geq 5, M \geq 5, C \geq 7.$

Xem đáp án

Xét hình đa diện là hình tứ diện thì kết quả về quan hệ số đỉnh và số mặt thỏa mãn đáp án C. Chọn C.

Câu 12:

Một hình đa diện có các mặt là những tam giác. Gọi là tổng số mặt và là tổng số cạnh của đa diện đó. Mệnh đề nào sau đây đúng

A. $3 C = 2 M$ .

B. $C = M + 2$ .

C. $M \geq C$ .

D. $3 M = 2 C$ .

Xem đáp án

Vì mỗi mặt là những tam giác nên có tổng số cạnh là Mỗi cạnh là cạnh chung của đúng hai mặt nên ta có hệ thức Chọn D.

Câu 13:

Hình đa diện nào dưới đây không có tâm đối xứng?

Media VietJack

A. Tứ diện đều

Media VietJack

B. Bát diện đều.

Media VietJack

C. Hình lập phương.

Media VietJack

D. Lăng trụ lục giác đều

Xem đáp án

Chọn A.

Câu 14:

Gọi

n_{1}, n_{2}, n_{3}

lần lượt là số trục đối xứng của khối tứ diện đều, khối chóp tứ giác đều và khối lập phương. Mệnh đề nào sau đây là đúng?

A.

n_{1} = 0, n_{2} = 0, n_{3} = 6.

B.

n_{1} = 0, n_{2} = 1, n_{3} = 9.

C.

n_{1} = 3, n_{2} = 1, n_{3} = 9.

D.

n_{1} = 0, n_{2} = 1, n_{3} = 3.

Xem đáp án

Khối tứ diện đều có 3 trục đối xứng (đi qua trung điểm của các cặp cạnh đối diện). Khối chóp tứ giác đều có 1 trục đối xứng (đi qua đỉnh và tâm của mặt tứ giác). Khối lập phương có 9 trục đối xứng (Loại 1: đi qua tâm của các mặt đối diện ; Loại 2: đi qua trung điểm các cặp cạnh đối diện). Chọn C.

Câu 15:

Hình chóp tứ giác đều có bao nhiêu mặt phẳng đối xứng?

A. 4 mặt phẳng.

B. 1 mặt phẳng.

C. 2 mặt phẳng.

D. 3 mặt phẳng.

Xem đáp án

Hình chóp tứ giác đều có 4 mặt phẳng đối xứng bao gồm:

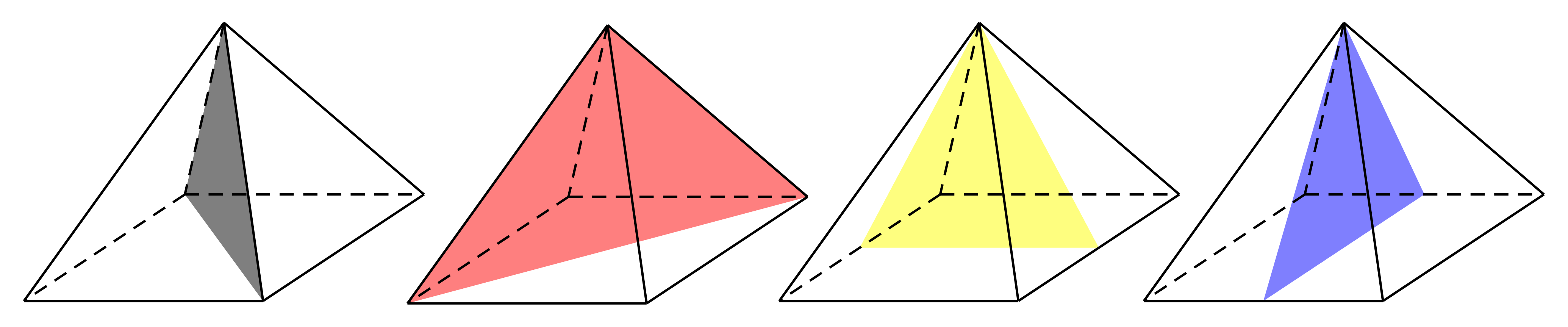
= 2 mặt phẳng đi qua đỉnh hình chóp và chứa đường trung bình của đáy.

= 2 mặt phẳng đi qua đỉnh hình chóp và chứa đường chéo của đáy.

Chọn A.

Câu 16:

Số mặt phẳng đối xứng của hình tứ diện đều là:

A. 4 mặt phẳng.

B. 6 mặt phẳng.

C. 8 mặt phẳng.

D. 10 mặt phẳng

Xem đáp án

Các mặt phẳng đối xứng của hình tứ diện đều là các mặt phẳng chứa một cạnh và qua trung điểm cạnh đối diện.

Vậy hình tứ diện đều có 6 mặt phẳng đối xứng. Chọn B.

Câu 17:

Hình lăng trụ tam giác đều có bao nhiêu mặt phẳng đối xứng ?

A. 4 mặt phẳng.

B. 1 mặt phẳng.

C. 2 mặt phẳng.

D. 3 mặt phẳng.

Xem đáp án

Hình lăng trụ tam giác đều có mặt phẳng đối xứng (hình vẽ bên dưới).

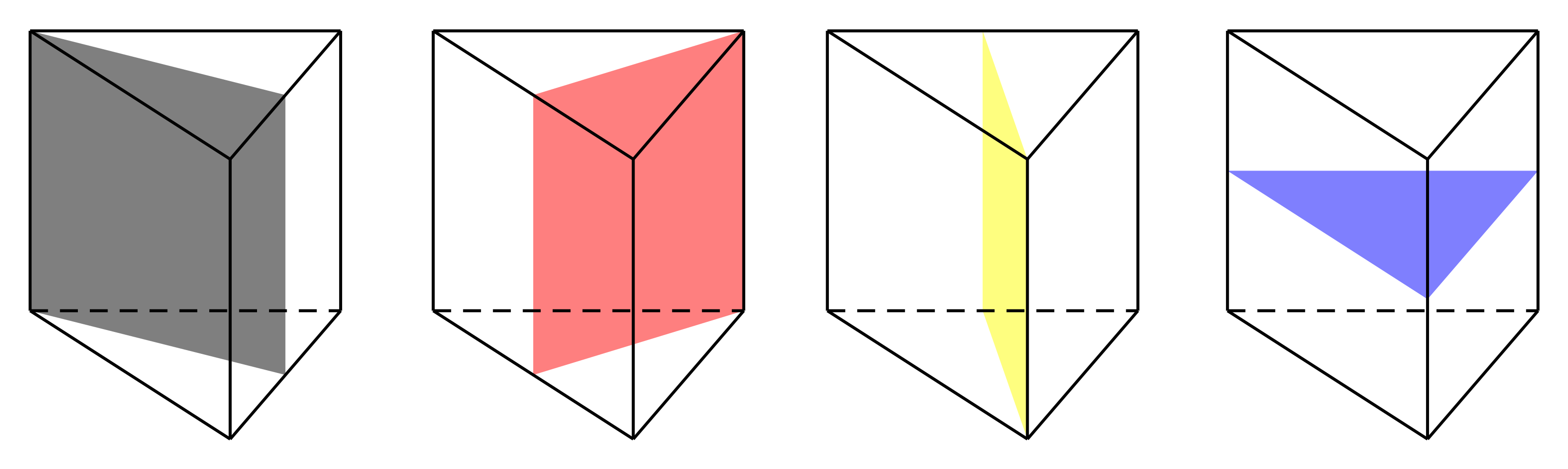
Chọn A.

Câu 18:

Hình hộp chữ nhật có ba kích thước đôi một khác nhau có bao nhiêu mặt phẳng đối xứng?

A. 4 mặt phẳng.

B. 6 mặt phẳng.

C. 9 mặt phẳng.

D. 3 mặt phẳng.

Xem đáp án

Hình hộp chữ nhật (không là hình lập phương) có các mặt phẳng đối xứng là các mặt các mặt phẳng trung trực của các cặp cạnh đối.

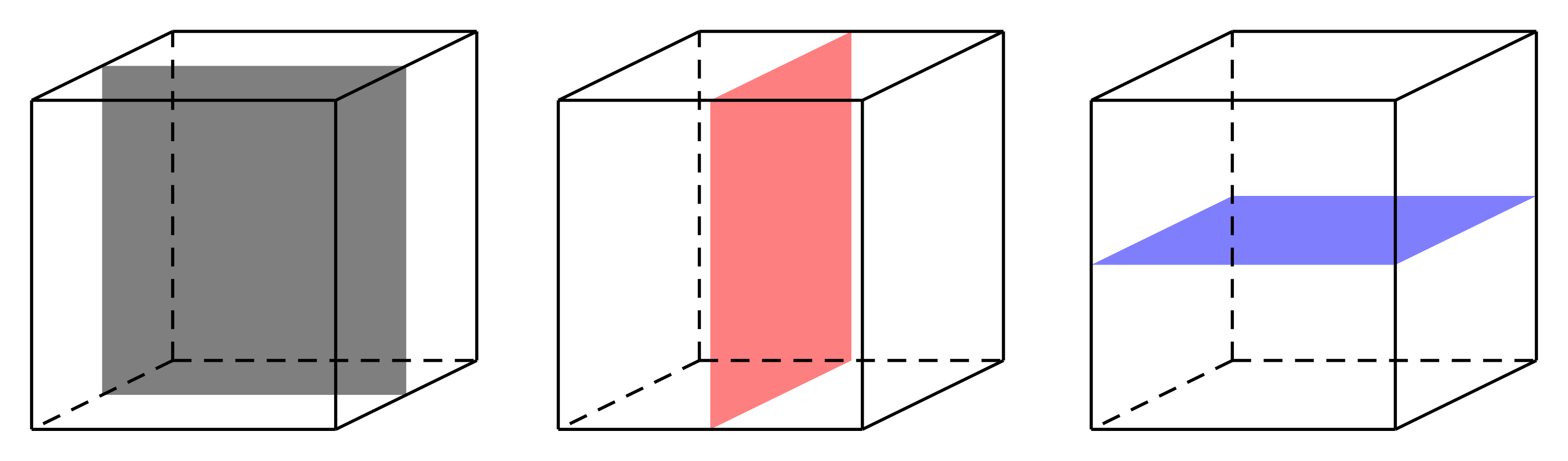
Chọn D.

Câu 19:

Một hình hộp đứng có đáy là hình thoi (không phải là hình vuông) có bao nhiêu mặt phẳng đối xứng?

A. 4 mặt phẳng.

B. 1 mặt phẳng.

C. 2 mặt phẳng.

D. 3 mặt phẳng.

Xem đáp án

Hình hộp đứng có đáy là hình thoi (không phải là hình chữ nhật) có 3 mặt phẳng đối xứng bao gồm:

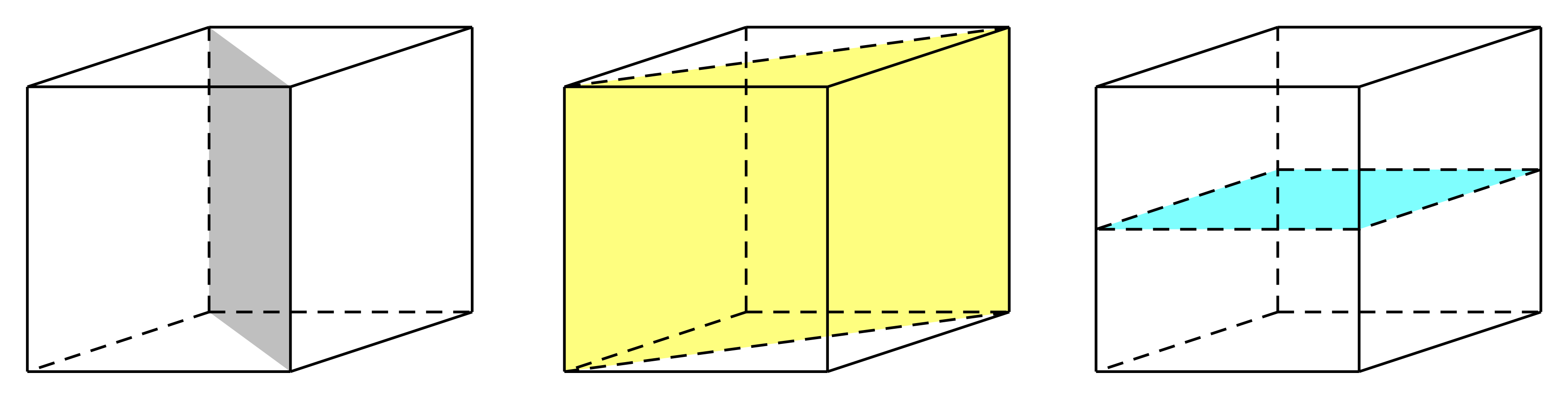
= 2 mặt phẳng chứa đường chéo của đáy và vuông góc với đáy.

= Một mặt phẳng là mặt phẳng trung trực của cạnh bên.

Chọn D.

Câu 20:

Hình lập phương có tất cả bao nhiêu mặt phẳng đối xứng?

A. 8 mặt phẳng.

B. 9 mặt phẳng.

C. 10 mặt phẳng.

D. 12 mặt phẳng.

Xem đáp án

Có 9 mặt đối xứng (như hình vẽ sau). Chọn B.

Câu 21:

Số mặt phẳng đối xứng của hình bát diện đều là:

A. 4 mặt phẳng.

B. 9 mặt phẳng.

C. 6 mặt phẳng.

D. 12 mặt phẳng

Xem đáp án

Gọi bát diện đều ABCDEF. Có 9 mặt phẳng đối xứng, bao gồm: 3 mặt phẳng (ABCD), (BEDF) , (AECF) và 6 mặt phẳng mà mỗi mặt phẳng là mặt phẳng trung trực của hai cạnh song song (chẳng hạn AB và CD).

Chọn B.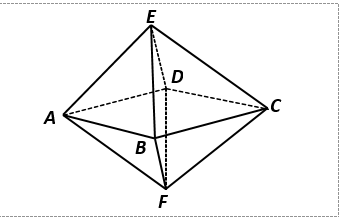

Câu 22:

Có tất cả bao nhiêu mặt phẳng cách đều bốn đỉnh của một tứ diện?

A. 1 mặt phẳng.

B. 4 mặt phẳng.

C. 7 mặt phẳng.

D. Có vô số mặt

Xem đáp án

Có loại mặt phẳng thỏa mãn đề bài là:

= Loại 1: Mặt phẳng qua trung điểm của cạnh bên có chung đỉnh. Có 4 mặt phẳng thỏa mãn loại này (vì có 4 đỉnh)

Nhận xét. Loại này ta thấy có 1 điểm nằm khác phía với 3 điểm còn lại.

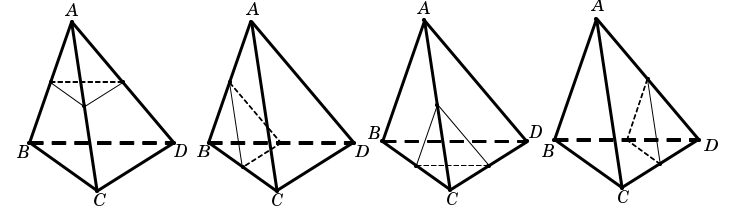
= Loại 2: Mặt phẳng qua trung điểm của cạnh ( cạnh này thuộc cặp cạnh, mỗi cặp cạnh là chéo nhau). Có mặt phẳng như thế.

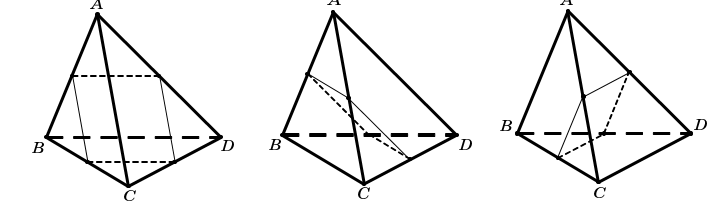
Nhận xét. Loại này ta thấy có 2 điểm nằm khác phía với 2 điểm còn lại.

Chọn C.

Câu 23:

Mặt phẳng $(A B^{'} C^{'})$ chia khối lăng trụ $A B C . A^{'} B^{'} C^{'}$ thành các khối đa diện nào ?

A. Một khối chóp tam giác và một khối chóp tứ giác.

B. Hai khối chóp tam giác.

C. Một khối chóp tam giác và một khối chóp ngũ giác.

D. Hai khối chóp tứ giác.

Xem đáp án

Dựa vào hình vẽ, ta thấy mặt phẳng $(A B^{'} C^{'})$ chia khối lăng trụ $A B C . A^{'} B^{'} C^{'}$ thành khối chóp tam giác $A . A^{'} B^{'} C^{'}$ và khối chóp tứ giác $A . B C C^{'} B^{'} .$

Chọn A.

Câu 24:

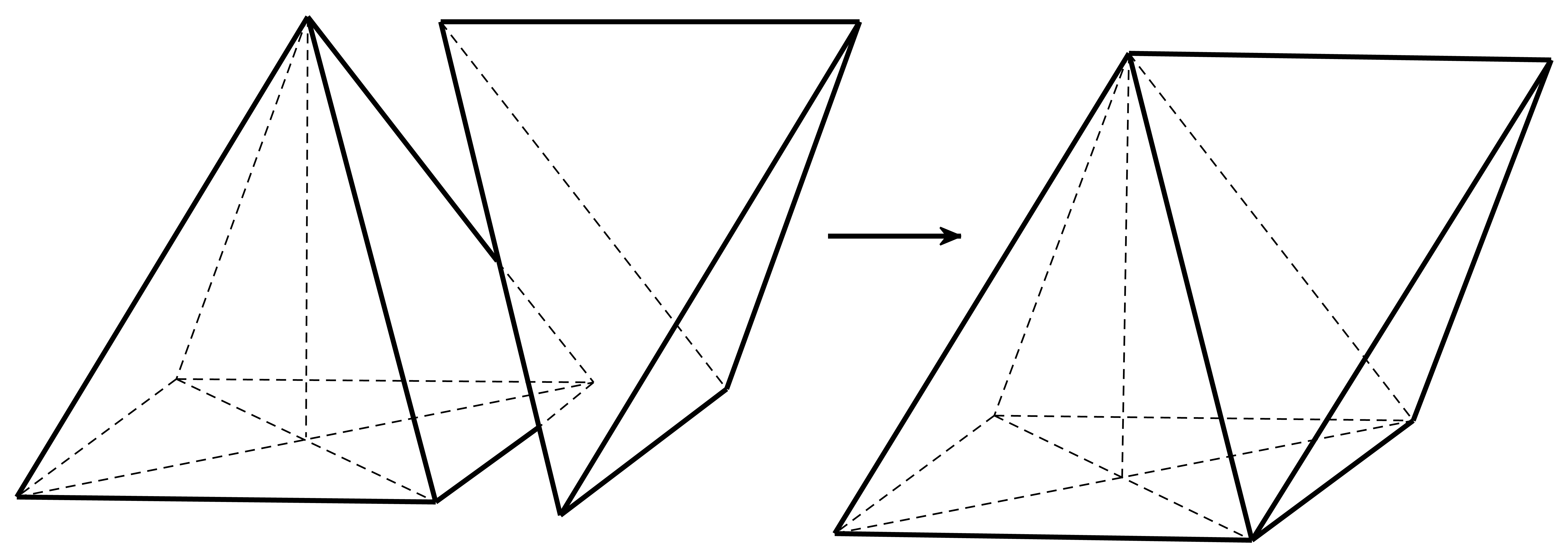
Lắp ghép hai khối đa diện $(H_{1}), (H_{2})$ để tạo thành khối đa diện (H), trong đó $(H_{1})$ là khối chóp tứ giác đều có tất cả các cạnh bằng a, $(H_{2})$ là khối tứ diện đều cạnh a sao cho một mặt của $(H_{1})$ trùng với một mặt của $(H_{2})$ như hình vẽ. Hỏi khối da diện (H) có tất cả bao nhiêu mặt?

A. 5

B. 7

C. 8

D.9

Xem đáp án

Khối đa diện có đúng 5 mặt. Chọn A.

Sai lầm hay gặp: Khối chóp tứ giác đều có 5 mặt. Khối tứ diện đều có 4 mặt.

Ghép hai hình lại như hình vẽ ta được khối đa diện (H) có 8 mặt

Câu 25:

Có thể chia một hình lập phương thành bao nhiêu khối tứ diện bằng nhau?

A. 2

B. 4

C. 6

D. 8

Xem đáp án

Lần lượt dùng mặt phẳng $(B D D^{'} B^{'})$ ta chia thành hai khối lập phương thành hai khối lăng trụ $A B D . A^{'} B^{'} D^{'}$ và $B C D . B^{'} C^{'} D^{'}$ .

= Với khối $A B D . A^{'} B^{'} D^{'}$ ta lần lượt dùng các mặt phẳng $(A B^{'} D^{'})$ và $(A B^{'} D)$ chia thành ba khối tứ diện bằng nhau.

= Tương tự với khối $B C D . B^{'} C^{'} D^{'}$ .

Vậy có tất cả 6 khối tứ diện bằng nhau. Chọn C.