Trắc nghiệm Toán 12 Chân trời sáng tạo Bài 2. Giá trị lớn nhất và giá trị nhỏ nhất của hàm số có đáp án
Trắc nghiệm Toán 12 Chân trời sáng tạo Bài 2. Giá trị lớn nhất và giá trị nhỏ nhất của hàm số có đáp án
-
102 lượt thi
-
20 câu hỏi
-
60 phút
Danh sách câu hỏi
Câu 1:
I. Nhận biết
Cho hàm số \[f\left( x \right)\] có đồ thị như hình bên. Giá trị lớn nhất của hàm số \[f\left( x \right)\] trên đoạn \[\left[ { - 3;2} \right]\] đạt tại \(x\) bằng
![Cho hàm số f ( x ) có đồ thị như hình bên. Giá trị lớn nhất của hàm số f ( x ) trên đoạn [ − 3 ; 2 ] đạt tại x bằng (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2024/10/blobid0-1729040580.png)
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Dựa vào đồ thị hàm số ta có \(\mathop {\max }\limits_{\left[ { - 3;2} \right]} f\left( x \right) = f\left( { - 3} \right) = 4\).
Câu 2:
Cho hàm số \[f\left( x \right)\] xác định, liên tục trên \(\mathbb{R}\) và có bảng biến thiên sau:
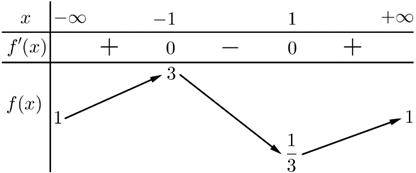
Giá trị nhỏ nhất của hàm số bằng :
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Dựa vào bảng biến thiên \(\mathop {\min }\limits_\mathbb{R} f\left( x \right) = f\left( 1 \right) = \frac{1}{3}\).
Câu 3:
Cho hàm số \(y = f\left( x \right)\) liên tục trên đoạn \(\left[ { - 2;2} \right]\) và có đồ thị trên đoạn \(\left[ { - 2;2} \right]\) như sau:
![Cho hàm số y = f ( x ) liên tục trên đoạn [ − 2 ; 2 ] và có đồ thị trên đoạn [ − 2 ; 2 ] như sau: Tìm giá trị lớn nhất của hàm số y = f ( x ) trên đoạn [ − 2 ; 2 ] . (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2024/10/blobid0-1729040628.png)
Tìm giá trị lớn nhất của hàm số \(y = f\left( x \right)\) trên đoạn \(\left[ { - 2;2} \right]\).
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
Dựa vào đồ thị ta có \(\mathop {\max }\limits_{\left[ { - 2;2} \right]} f\left( x \right) = 3\).
Câu 4:
Cho hàm số \(y = f\left( x \right)\) có bảng biến thiên như sau:
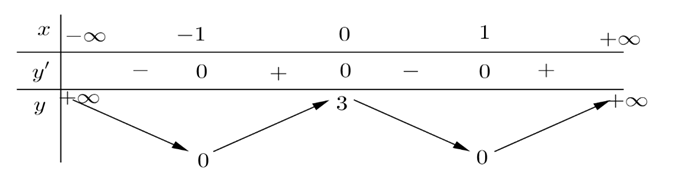
Khẳng định nào sau đây đúng?
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
Dựa vào bảng biến thiên ta có hàm số có GTNN bằng 0.
Câu 5:
Cho hàm số \(y = f(x)\) liên tục trên đoạn \(\left[ { - 1;3} \right]\) và có bảng biến thiên như sau
![Cho hàm số y = f ( x ) liên tục trên đoạn [ − 1 ; 3 ] và có bảng biến thiên như sau Giá trị lớn nhất của hàm số y = f ( x ) trên đoạn [ − 1 ; 3 ] bằng (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2024/10/blobid0-1729040661.png)
Giá trị lớn nhất của hàm số \(y = f(x)\) trên đoạn \(\left[ { - 1;3} \right]\) bằng
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
Dựa vào bảng biến thiên ta có giá trị lớn nhất của hàm số \(y = f(x)\) trên đoạn \(\left[ { - 1;3} \right]\) bằng \(f\left( 0 \right)\).
Câu 6:
II. Thông hiểu
Cho hàm số \[y = f(x)\] liên tục trên đoạn \[\left[ { - 3;1} \right]\]và có đồ thị như hình vẽ. Gọi \[M\] và \[m\]lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số đã cho trên đoạn \[\left[ { - 3;1} \right]\]. Giá trị của \[M - m\] bằng
![Cho hàm số y = f ( x ) liên tục trên đoạn [ − 3 ; 1 ] và có đồ thị như hình vẽ. Gọi M và m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số đã cho trên đoạn [ − 3 ; 1 ] . Giá trị của M − m bằng (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2024/10/blobid0-1729040708.png)
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: A
\(M = \mathop {\max }\limits_{\left[ { - 3;1} \right]} f\left( x \right) = 5;m = \mathop {\min }\limits_{\left[ { - 3;1} \right]} f\left( x \right) = - 1\). Do đó M – m = 5 + 1 = 6.
Câu 7:
Tìm giá trị lớn nhất \(M\)và giá trị nhỏ nhất \(m\)của hàm số \(y = {x^4} - 8{x^2} + 3\) trên đoạn \(\left[ { - 1;1} \right]\) .
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
Ta có y' = 4x3 – 16x; y' = 0 x = 0 (vì chỉ tìm x (−1; 1)).
Có y(0) = 3; y(1) = −4; y(−1) = −4.
Do đó M = 3 và m = −4.
Câu 8:
Giá trị lớn nhất và nhỏ nhất của hàm số \[y = {x^3}\; - 12x + 1\] trên đoạn \[\left[ { - 2;{\rm{ }}3} \right]\] lần lượt là :
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
Ta có y' = 3x2 – 12 = 0 x = 2 hoặc x = −2.
Ta có y(−2) = 17; y (2) = −15; y(3) = −8.
Vậy giá trị nhỏ nhất của hàm số là −15 và giá trị lớn nhất của hàm số là 17.
Câu 9:
Tìm giá trị lớn nhất của hàm số \(f\left( x \right) = \frac{{x - 2}}{{x + 1}}\) trên đoạn \(\left[ {0;\,2} \right]\).
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
Xét trên đoạn \(\left[ {0;\,2} \right]\), ta có \(f'\left( x \right) = \frac{3}{{{{\left( {x + 1} \right)}^2}}} > 0\).
Suy ra \(GTLN:\,\,\mathop {\max }\limits_{{\rm{[}}0;\,2]} \,f(x) = f(2) = 0\).
Câu 10:
Tìm giá trị nhỏ nhất của hàm số \[y = {x^4} - 2{x^2} + 3\] trên đoạn \[\left[ { - 3;\,2} \right]\].
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
Ta có: \[y' = 4{x^3} - 4x = 0 \Leftrightarrow \left[ \begin{array}{l}x = 0\\x = \pm 1\end{array} \right.\].
\[y\left( { - 3} \right) = 66;\,y\left( 2 \right) = 11;\,\,y\left( 0 \right) = 3;\,\,y\left( 1 \right) = 2;\,\,y\left( { - 1} \right) = 2\].
\[ \Rightarrow {y_{\min }} = 2\].
Câu 11:
Cho hàm số \(f\left( x \right) = \frac{{{x^2} - 4x + 7}}{{x - 1}}\). Gọi \(M,\;m\) lần lượt là giá trị lớn nhất và nhỏ nhất của hàm số trên đoạn \[\left[ {2;4} \right]\]. Tính \(M + m\) ?
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
Có \(f'\left( x \right) = \frac{{\left( {2x - 4} \right)\left( {x - 1} \right) - \left( {{x^2} - 4x + 7} \right)}}{{{{\left( {x - 1} \right)}^2}}}\)\( = \frac{{{x^2} - 2x - 3}}{{{{\left( {x - 1} \right)}^2}}}\);
\(f'\left( x \right) = 0 \Leftrightarrow \frac{{{x^2} - 2x - 3}}{{{{\left( {x - 1} \right)}^2}}} = 0 \Leftrightarrow \left[ \begin{array}{l}x = 3\\x = - 1\end{array} \right.\).
Vì x ∈ [2; 4] nên chọn x = 3.
Ta có y(2) = 3; y(3) = 2; \(y\left( 4 \right) = \frac{7}{3}\).
Do đó M = 3 và m = 2 suy ra M + m = 5.
Câu 12:
Giá trị lớn nhất của hàm số \[f\left( x \right) = - {x^4} + 2{x^2} + 3\] trên khoảng \[\left( { - \infty ;\,2} \right)\] bằng
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
Ta có f'(x) = −4x3 + 4x; f'(x) = 0 x = −1 hoặc x = 0 hoặc x = 1.
Ta có \[\mathop {\lim }\limits_{x \to - \infty } f\left( x \right) = \mathop {\lim }\limits_{x \to - \infty } \left( { - {x^4} + 2{x^2} + 3} \right) = - \infty \]; \[\mathop {\lim }\limits_{x \to {2^ - }} f\left( x \right) = \mathop {\lim }\limits_{x \to {2^ - }} \left( { - {x^4} + 2{x^2} + 3} \right) = - 5\].
Ta có bảng biến thiên
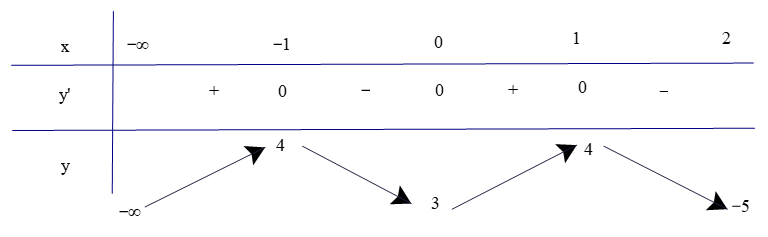
Vậy giá trị lớn nhất của hàm số là 4.
Câu 13:
Cho hàm số \(f\left( x \right)\) liên tục trên \(\left[ { - 1;5} \right]\) và có đồ thị như sau
![Cho hàm số f ( x ) liên tục trên [ − 1 ; 5 ] và có đồ thị như sau Tổng giá trị lớn nhất và giá trị nhỏ nhất của hàm số f ( x ) trên đoạn [ − 1 ; 5 ] bằng (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2024/10/blobid0-1729040859.png)
Tổng giá trị lớn nhất và giá trị nhỏ nhất của hàm số \(f\left( x \right)\) trên đoạn \(\left[ { - 1;5} \right]\)bằng
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
Dựa vào đồ thị hàm số ta có \[\mathop {\max }\limits_{\left[ { - 1;5} \right]} f\left( x \right) = 3;\mathop {\min }\limits_{\left[ { - 1;5} \right]} f\left( x \right) = - 2\]. Do đó tổng bằng 1.
Câu 14:
Gọi m là giá trị nhỏ nhất của hàm số \(y = x + \frac{4}{x}\) trên khoảng (0; +∞). Tìm m
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
Có \(y' = 1 - \frac{4}{{{x^2}}}\); \(y' = 0 \Leftrightarrow x = 2\)(vì x > 0).
Bảng biến thiên
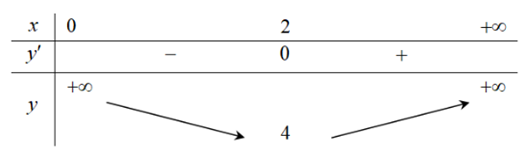
Dựa vào bảng biến thiên ta có m = 4.
Câu 15:
Giá trị nhỏ nhất của hàm số \(y = \sqrt {4 - x} + \sqrt 3 \) trên tập xác định của nó là
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
Ta có D = (−∞; 4].
Có \(y' = \frac{{ - 1}}{{2\sqrt {4 - x} }} < 0,\forall x \in D\).
Bảng biến thiên
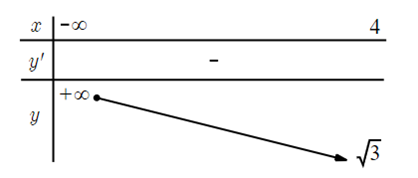
Dựa vào bảng biến thiên ta có giá trị nhỏ nhất của hàm số là \(\sqrt 3 \).
Câu 16:
III. Vận dụng
Cho hàm số \(y = \frac{{x + m}}{{x - 2}}\) thỏa mãn \(\mathop {\min }\limits_{\left[ {3;5} \right]} y = 4\). Mệnh đề nào dưới đây đúng
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
Hàm số \(y = \frac{{x + m}}{{x - 2}}\) xác định và liên tục trên \(\left[ {3;5} \right]\). Ta có \(y' = \frac{{ - 2 - m}}{{{{\left( {x - 2} \right)}^2}}}\).
+ Xét \( - 2 - m > 0 \Leftrightarrow m < - 2\,\,\left( * \right)\).
Khi đó hàm số đồng biến trên \(\left[ {3;5} \right]\).
Suy ra \(\mathop {\min }\limits_{\left[ {3;5} \right]} y = y\left( 3 \right) = 3 + m\). Do đó \(3 + m = 4 \Leftrightarrow m = 1\)( không thỏa \(\left( * \right)\)).
+ Xét \( - 2 - m < 0 \Leftrightarrow m > - 2\,\,\,\left( {**} \right)\).</>
Khi đó hàm số nghịch biến trện \(\left[ {3;5} \right]\).
Suy ra \(\mathop {\min }\limits_{\left[ {3;5} \right]} y = y\left( 5 \right) = \frac{{5 + m}}{3}\). Do đó \(\frac{{5 + m}}{3} = 4 \Leftrightarrow m = 7\)( thỏa \(\left( {**} \right)\)).
Vậy \(m = 7 > 5\).
Câu 17:
Tích giá trị lớn nhất và giá trị nhỏ nhất của hàm số \(y = x + \sqrt {4 - {x^2}} \).
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Điều kiện: −2 ≤ x ≤ 2.
Có \(y' = 1 - \frac{x}{{\sqrt {4 - {x^2}} }}\);
\(y' = 0 \Leftrightarrow 1 - \frac{x}{{\sqrt {4 - {x^2}} }} = 0\)\( \Leftrightarrow x = \sqrt {4 - {x^2}} \)\( \Leftrightarrow \left\{ \begin{array}{l}x \ge 0\\{x^2} = 4 - {x^2}\end{array} \right.\)\( \Leftrightarrow x = \sqrt 2 \).
Có y(−2) = −2; y(2) = 2; \(y\left( {\sqrt 2 } \right) = 2\sqrt 2 \).
Vậy \(\mathop {\min }\limits_{\left[ { - 2;2} \right]} y = - 2;\mathop {\max }\limits_{\left[ { - 2;2} \right]} y = 2\sqrt 2 \). Do đó tích của giá trị lớn nhất và giá trị nhỏ nhất là \( - 4\sqrt 2 \).
Câu 18:
Một chất điểm chuyển động theo quy luật S = 6t2 – t3, vận tốc v(m/s) của chuyển động đạt giá trị lớn nhất tại thời điểm t(s) bằng
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
Vận tốc của chuyển động là v(t) = s' = 12t – 3t2, t > 0.
Có v'(t) = −6t + 12; v'(t) = 0 t = 2.
Bảng biến thiên
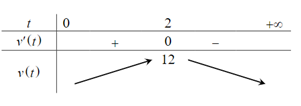
Dựa vào bảng biến thiên ta thấy vận tốc v(m/s) của chuyển động đạt giá trị lớn nhất tại thời điểm t = 2.
Câu 19:
Một vật chuyển động theo quy luật \(s = - \frac{1}{3}{t^3} + 6{t^2}\) với t (giây) là khoảng thời gian tính từ khi vật bắt đầu chuyển động và s (mét) là quãng đường vật di chuyển được trong khoảng thời gian đó. Hỏi trong khoảng thời gian 9 giây kể từ khi bắt đầu chuyển động, vận tốc lớn nhất của vật đạt được bằng bao nhiêu?
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
Ta có v = s' = −t2 + 12t; v' = −2t + 12; v' = 0 t = 6.
Bảng biến thiên
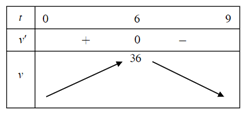
Từ bảng biến thiên, ta thấy vận tốc lớn nhất của vật là 36 m/s.
Câu 20:
Công suất P (đơn vị W) của một mạch điện được cung cấp bởi một nguồn pin 12V được cho bởi công thức P = 12I – 0,5I2 với I (đơn vị A) là cường độ dòng điện. Tìm công suất tối đa của mạch điện.
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
Xét hàm số P = 12I – 0,5I2 với I ≥ 0.
Có P' = 12 – I; P' = 0 I = 12.
Bảng biến thiên
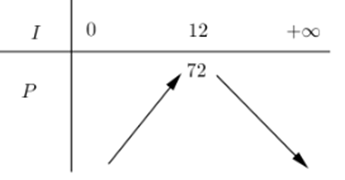
Vậy công suất tối đa của mạch điện là 72 (W) đạt được khi cường độ dòng điện là 12 (A).
