Trắc nghiệm Toán 12 Lũy thừa- Hàm số lũy thừa có đáp án (Mới nhất)
-
1331 lượt thi
-
15 câu hỏi
-
50 phút
Danh sách câu hỏi
Câu 1:
 Xem đáp án
Xem đáp án
Áp dụng lý thuyết ![]() Lũy thừa với số mũ không nguyên thì cơ số phải dương
Lũy thừa với số mũ không nguyên thì cơ số phải dương![]() .
.
Do đó hàm số xác định khi . Chọn D.
Câu 2:
Tìm tập xác định D của hàm số .
 Xem đáp án
Xem đáp án
Áp dụng lý thuyết "Lũy thừa với số mũ nguyên âm thì cơ số phải khác 0".
Do đó hàm số đã cho xác định khi Chọn B.
Câu 3:
Tìm tập xác định D của hàm số .
 Xem đáp án
Xem đáp án
Áp dụng lý thuyết ![]() Lũy thừa với số mũ không nguyên thì cơ số phải dương
Lũy thừa với số mũ không nguyên thì cơ số phải dương![]() .
.
Do đó hàm số đã cho xác định khi
. Chọn B.
Câu 7:
Rút gọn biểu thức với
 Xem đáp án
Xem đáp án
Cách CASIO. Chọn ví dụ như chẳng hạn.
Tính giá trị rồi lưu vào A
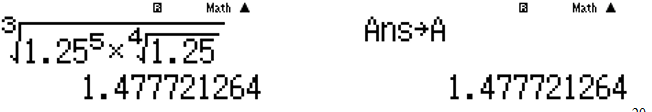
Tiếp theo ta tính hiệu, ví dụ như đáp án A ta cần tính . Nếu màn hình máy tính xuất hiện kết quả bằng 0 thì chứng tỏ đáp án A đúng.
Đáp số chính là B. Chọn B.
Câu 13:
Tìm tất cả các giá trị của a thỏa mãn .
 Xem đáp án
Xem đáp án
Ta có , kết hợp với . Suy ra hàm số đặc trưng đồng biến cơ số . Chọn A.
Câu 14:
Một người lần đầu gửi vào ngân hàng 100 triệu đồng với kì hạn 3 tháng, lãi suất 2% một quý. Biết rằng nếu không rút tiền ra khỏi ngân hàng thì cứ sau mỗi quý số tiền lãi sẽ được nhập vào gốc để tính lãi cho quý tiếp theo. Sau đúng 6 tháng, người đó gửi thêm 100 triệu đồng với kỳ hạn và lãi suất như trước đó. Tổng số tiền người đó nhận được 1 năm sau khi gửi tiền (cả vốn lẫn lãi) gần nhất với kết quả nào sau đây?
 Xem đáp án
Xem đáp án
Số tiền nhận về sau 1 năm của 100 triệu gửi trước là triệu.
Số tiền nhận về sau 6 tháng của 100 triệu gửi sau là triệu.
Vậy tổng số tiền là triệu.Chọn C.
Câu 15:
Bác An đem gửi tổng số tiền 320 triệu đồng ở hai loại kỳ hạn khác nhau. Bác gửi 140 triệu đồng theo kỳ hạn ba tháng với lãi suất 2,1% một quý. Số tiền còn lại bác An gửi theo kỳ hạn một tháng với lãi suất 0,73% một tháng. Biết rằng nếu không rút tiền ra khỏi ngân hàng thì cứ sau mỗi kỳ hạn số tiền lãi sẽ được nhập vào gốc để tính lãi cho kỳ hạn tiếp theo. Sau 15 tháng kể từ ngày gửi bác An đi rút tiền. Tính gần đúng đến hàng đơn vị tổng số tiền lãi thu được của bác An.
 Xem đáp án
Xem đáp án
Số tiền nhận về sau 15 tháng của 140 triệu gửi trước là triệu.
Số tiền nhận về sau 15 tháng của 180 triệu gửi sau là triệu.
Suy ra tổng số tiền cả vốn lẫn lãi mà bác An thu được là
triệu.
Suy ra số tiền lãi: đồng. Chọn D.
