20 câu trắc nghiệm Toán 12 Kết nối tri thức Bài 18. Xác suất có điều kiện có đáp án
20 câu trắc nghiệm Toán 12 Kết nối tri thức Bài 18. Xác suất có điều kiện có đáp án
-
112 lượt thi
-
20 câu hỏi
-
60 phút
Danh sách câu hỏi
Câu 1:
I. Nhận biết
Cho hai biến cố \(A\) và \(B\) bất kì, với \(P\left( B \right) > 0\). Chọn khẳng định sai trong các khẳng định dưới đây:
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
Câu 2:
Cho hai biến cố \(A\) và \(B\) là hai biến cố độc lập và \(P\left( A \right) > 0,P\left( B \right) > 0\). Chọn khẳng định sai trong các khẳng định dưới đây.
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Câu 3:
Cho hai biến cố \(A\) và \(B\) là hai biến cố độc lập, với \(P\left( A \right) = 0,2024\), \(P\left( B \right) = 0,2025\). Tính \(P\left( {A|B} \right)\).
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
Do \(A\) và \(B\) là hai biến cố độc lập, nên ta có:
\(P\left( {A|B} \right) = \frac{{P\left( {AB} \right)}}{{P\left( B \right)}} = \frac{{P\left( A \right).P\left( B \right)}}{{P\left( B \right)}} = P\left( A \right)\),
Suy ra \(P\left( {A|B} \right) = P\left( A \right) = 0,2024.\)
Câu 4:
Cho hai biến cố \(A\) và \(B\) là hai biến cố độc lập, với \(P\left( A \right) = 0,24\), \(P\left( B \right) = 0,25\). Tính \(P\left( {B|\overline A } \right)\).
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
Ta có: \(P\left( {B|\overline A } \right) = P\left( B \right) = 0,25.\)
Câu 5:
Cho hai biến cố \(A\) và \(B\) là hai biến cố độc lập, với \(P\left( A \right) = 0,6\), \(P\left( B \right) = 0,7,\) \(P\left( {A \cap B} \right) = 0,3\). Tính \(P\left( {A|B} \right)\).
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
Ta có: \(P\left( {A|B} \right) = \frac{{P\left( {A \cap B} \right)}}{{P\left( B \right)}} = \frac{{0,3}}{{0,7}} = \frac{3}{7}.\)
Câu 6:
II. Thông hiểu
Cho hai biến cố \(A\) và \(B\) với \(P\left( A \right) = 0,8\), \(P\left( B \right) = 0,65\), \(P\left( {A \cap \overline B } \right) = 0,55\). Tính \(P\left( {A \cap B} \right)\).
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
Ta có: \(P\left( {A \cap B} \right) + P\left( {A \cap \overline B } \right) = P\left( A \right)\)
\(P\left( {A \cap B} \right) = P\left( A \right) - P\left( {A \cap \overline B } \right) = 0,8 - 0,55 = 0,25.\)
Câu 7:
Một hộp chứa 4 quả bóng được đánh số từ 1 đến 4. An lấy ngẫu nhiên một quả bóng, bỏ ra ngoài, rồi lấy tiếp một quả bóng nữa. Xét các biến cố:
A: “Quả bóng lấy ra lần đầu có số chẵn”.
B: “Quả bóng lấy ra lần đầu có số lẻ”.
Tính xác suất có điều kiện \(P\left( {A|B} \right).\)
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Xác suất để quả bóng đầu tiên là số chẵn là: \(P\left( A \right) = \frac{2}{4} = \frac{1}{2}.\)
Xác suất để quả bóng đầu tiên có số lẻ là: \(P\left( B \right) = \frac{2}{4} = \frac{1}{2}.\)
Khi đã lấy được một quả bóng lẻ (là 1 hoặc 3), chúng ta có 3 quả còn lại trong hộp và trong đó có 2 quả đánh số chẵn.
Do đó, P(A | B) = \(\frac{2}{3}.\)
Câu 8:
Một hộp kín đựng 20 tấm thẻ giống nhau được đánh số từ 1 đến 20. Một người rút ngẫu nhiên ra một tấm thẻ từ trong hộp. Người đó được thông báo rằng thẻ rút ra mang số chẵn. Tính xác suất để người đó rút được thẻ số 10.
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
Theo đề bài, hộp có 20 tấm thẻ được đánh số từ 1 đến 20 nên có 10 tấm thẻ mang số chẵn trong hộp.
Biết rằng thẻ rút ra là số chẵn, xác suất để người đó rút ra được thẻ số 10 là \(\frac{1}{{10}} = 0,1.\)
Câu 9:
Một công ty xây dựng đấu thầu hai dự án độc lập. Khả năng thắng thầu của các dự án 1 là 0,6 và dự án 2 là 0,7. Tính xác suất để công ty thắng thầu đúng 1 dự án.
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Gọi A là biến cố: “Thắng thầu dự án 1”,
Gọi B là biến cố: “Thắng thầu dự án 2”.
Theo đề bài, P(A) = 0,6 nên \(P\left( {\overline A } \right) = 0,4\); P(B) = 0,7 nên \(P\left( {\overline B } \right) = 0,3\) với hai biến cố A, B độc lập.
Gọi C là biến cố “thắng thầu đúng 1 dự án”.
P(C) = \(P\left( A \right).P\left( {\overline B } \right) + P\left( {\overline A } \right).P\left( B \right)\) = 0,6.0,3 + 0,4.0,7 = 0,46.
Câu 10:
Cho hai biến cố A và B, với \(P\left( A \right) = 0,6\), \(P\left( B \right) = 0,7\), \(P\left( {A \cap B} \right) = 0,3\). Tính \(P\left( {\overline A \cap B} \right).\)
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Ta có: \(P\left( {\overline A \cap B} \right) = P\left( {\overline A |B} \right).P\left( B \right)\)
Mà \(P\left( {\overline A |B} \right) = 1 - P\left( {A|B} \right) = 1 - \frac{{P\left( {A \cap B} \right)}}{{P\left( B \right)}} = 1 - \frac{{0,3}}{{0,7}} = \frac{4}{7}.\)
Do đó, \(P\left( {\overline A \cap B} \right) = P\left( {\overline A |B} \right).P\left( B \right) = \frac{4}{7}.0,7 = 0,4 = \frac{2}{5}.\)
Câu 11:
Gieo lần lượt hai con xúc xắc cân đối và đồng chất. Tính xác suất để tổng số chấm xuất hiện trên hai con xúc xắc bằng 6. Biết rằng con xúc xắc thứ nhất xuất hiện mặt 4 chấm.
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
Gọi A là biến cố “Con xúc xắc thứ nhất xuất hiện mặt 4 chấm”
Gọi B là biến cố “Tổng số chấm xuất hiện trên 2 con xúc xắc bằng 6”.
Khi con xúc xắc thứ nhất đã xuất hiện mặt 4 chấm thì lần thứ hai xuất hiện mặt 2 chấm.
Do đó chỉ có 1 trường hợp thỏa mãn.
Vậy P = \(\frac{1}{6}.\)
Câu 12:
Trong một hợp có 4 viên bi: 2 viên màu đỏ, 1 viên màu xanh và 1 viên màu vàng. Bạn rút ra 2 viên bi liên tiếp mà không thay thế. Tính xác suất để viên bi đầu tiên là xanh và viên thứ hai là đỏ.
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Xác suất để viên bi đầu tiên là màu xanh là \(\frac{1}{4}.\)
Xác suất để viên bi thứ hai là mãu đỏ là \(\frac{2}{3}.\)
Suy ra xác suất để viên bi đầu tiên là xanh và viên bi thứ hai là đỏ là: \(\frac{1}{4}.\frac{2}{3} = \frac{1}{6}.\)
Câu 13:
Gieo hai con xúc xắc cân đối, đồng chất. Tính xác suất để tổng số chấm xuất hiện trên hai con xúc xắc lớn hơn 10, biết rằng có ít nhất một con đã ra mặt 5 chấm.
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
Theo đề bài, khi gieo hai con xúc sắc thì tổng số chấm thu được trên hai con xúc xắc lớn hơn 10, tức là tổng của chúng bằng 11 hoặc 12.
Gọi A là biến cố: “Có ít nhất một con xúc xắc xuất hiện mặt 5 chấm”.
B là biến cố: “Tổng số chấm xuất hiện trên hai con xúc xắc lớn hơn 10”.
Ta có: \(P\left( A \right)\)= 1 – \(P\left( {\overline A } \right)\) = 1 – \({\left( {\frac{5}{6}} \right)^2} = \frac{{11}}{{36}}.\)
Biến cố B có các trường hợp: (4; 6), (6; 4), (5; 5), (5; 6), (6; 5), (6; 6).
Biến cố A ∩ B có 3 trường hợp xảy ra: (5; 6), (6; 5).
Do đó P(AB) = \(\frac{2}{{36}}.\)
Vậy P(B | A) = \(\frac{{P\left( {AB} \right)}}{{P\left( A \right)}} = \frac{2}{{36}}:\frac{{11}}{{36}} = \frac{2}{{11}}.\)
Câu 14:
Một hộp chứa 8 bi trắng, 2 bi đỏ. Lần lượt lấy từng viên bi. Giả sử lần đầu tiên bốc được bi trắng. Xác định xác suất lần thứ hai bốc được bi đỏ.
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
Gọi A là biến cố “Lần một bốc được bi trắng”.
B là biến cố “Lần thứ hai bốc được bi đỏ”.
Xác suất để lần hai bốc được bi đỏ biết lần một bốc được bi trắng là P(B | A).
Ta có: P(A) = \(\frac{{C_8^1}}{{C_{10}^1}} = \frac{4}{5}\); P(AB) = \(\frac{{C_8^1}}{{C_{10}^1}}.\frac{{C_2^1}}{{C_9^1}} = \frac{8}{{45}}.\)
Do đó, P(B | A) = \(\frac{{P\left( {A \cap B} \right)}}{{P\left( A \right)}} = \frac{8}{{45}}:\frac{4}{5} = \frac{2}{9}.\)
Câu 15:
Cho hai biến cố \(A\) và \(B\) là hai biến cố độc lập, với \(P\left( A \right) = 0,7\), \(P\left( {\overline B } \right) = 0,6.\) Khi đó:
a) \(P\left( {A|B} \right) = 0,6.\)
b) \(P\left( {B|\overline A } \right) = 0,4.\)
c) \(P\left( {\overline A |B} \right) = 0,45.\)
d) \(P\left( {\overline B |\overline A } \right) = 0,6.\)
Số mệnh đề đúng trong các mệnh đề trên là
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Theo đề, ta có: \(P\left( A \right) = 0,7\) nên \(P\left( {\overline A } \right) = 1 - P\left( A \right) = 1 - 0,7 = 0,3.\)
\(P\left( {\overline B } \right) = 0,6\) nên \(P\left( {\overline B } \right) = 1 - P\left( B \right) = 0,4\).
a) Do A và B độc lập nên P(A | B) = P(A) = 0,7 ≠ 0,6.
Do đó ý a sai.
b) Do A và B độc lập nên A và \(\overline B \) độc lập, B và \(\overline A \) độc lập, \(\overline B \) và \(\overline A \) độc lập.
Có A và \(\overline B \) độc lập nên \(P\left( {B|\overline A } \right) = P\left( B \right) = 0,4.\)
Do đõ ý b đúng.
c) Do B và \(\overline A \) độc lập nên \(P\left( {\overline A |B} \right) = P\left( {\overline A } \right) = 0,3.\)
Do đó ý c đúng.
d) Do \(\overline B \) và \(\overline A \) độc lập nên \(P\left( {\overline B |\overline A } \right) = P\left( {\overline B } \right) = 0,6.\)
Do đó, ý d đúng.
Câu 16:
III. Vận dụng
Lớp 12A có 30 học sinh, trong đó có 17 bạn nữ còn lại là nam. Có 3 bạn tên Hiền, trong đó có 1 bạn nữ bà 2 bạn nam. Thầy giáo gọi ngẫu nhiên một bạn lên bảng, khi đó:
a) Xác suất để có tên hiền là \(\frac{1}{{10}}.\)
b) Xác suất để có tên Hiền, biết bạn đó là nữ là \(\frac{3}{{17}}.\)
c) Xác suất để có tên Hiền, biết bạn đó là nam là \(\frac{2}{{13}}.\)
d) Nếu thầy giáo gọi 1 bạn có tên Hiền lên bảng thì xác suất để bạn đó là nam là \(\frac{3}{{17}}.\)
Số mệnh đề đúng trong các mệnh đề trên là
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
Gọi A là biến cố: “Học sinh được gọi lên bảng tên là Hiền”
Gọi B là biến cố: “Học sinh được chọn mang giới tính nữ”.
a) Xác suất để học sinh được gọi tên là Hiền là: P(A) = \(\frac{3}{{30}} = \frac{1}{{10}}.\)
Vậy ý a đúng.
b) Xác suất để thầy giáo gọi bạn đó lên bảng tên Hiền và với điều kiện bạn đó là nữ là
P(A | B).
Ta có: P(B) = \(\frac{{17}}{{30}}\), P(AB) = \(\frac{1}{{30}}\).
Do đó, P(A | B) = \(\frac{{P\left( {A \cap B} \right)}}{{P\left( B \right)}} = \frac{1}{{30}}:\frac{{17}}{{30}} = \frac{1}{{17}}\).
Vậy ý b sai.
c) Gọi C là biến cố “Học sinh được chọn mang giới tính nam”.
Xác suất thầy giáo gọi bạn đó lên bảng có tên Hiền, với điều kiện bạn đó là nam là
P(A | C).
Ta có: P(C) = \(\frac{{13}}{{30}}\), P(A ∩ C) = \(\frac{2}{{30}}\). Do đó: P(A | C) = \(\frac{{P\left( {A \cap C} \right)}}{{P\left( C \right)}} = \frac{2}{{30}}:\frac{{13}}{{30}} = \frac{2}{{13}}.\)
Do đó, ý c đúng.
d) Nếu thầy giáo gọi một bạn có tên Hiền lên bảng thì xác suất bạn đó là nam là
P(C | A) = \(\frac{{P\left( {A \cap C} \right)}}{{P\left( A \right)}} = \frac{2}{{30}}:\frac{3}{{30}} = \frac{2}{3}.\)
Vậy ý d sai.
Câu 17:
Lớp 10A có 35 học sinh, mỗi học sinh đều giỏi ít nhất một trong hai môn toán hoặc Văn. Biết rằng có 23 học sinh giỏi Toán và có 20 học sinh giỏi môn Văn. Chọn ngẫu nhiên một học sinh của lớp 10A. Khi đó:
a) Xác suất để học sinh được chọn giỏi Toán biết rằng học sinh đó cũng giỏi Văn là \(\frac{2}{5}.\)
b) Xác suất để học sinh được chọn giỏi môn Văn biết rằng học sinh đó cũng giỏi môn Toán bằng \(\frac{8}{{23}}.\)
c) Xác suất để học sinh được chọn không giỏi môn Toán biết rằng học sinh đó giỏi môn Văn bằng \(\frac{{15}}{{23}}.\)
d) Xác suất để học sinh được chọn không giỏi môn Văn biết rằng học sinh đó giỏi môn Toán bằng \(\frac{3}{5}.\)
Số mệnh đề đúng trong các mệnh đề trên là:
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
Gọi A là biến cố: “Học sinh được chọn giỏi môn Toán”
B là biến cố: “Học sinh được chọn giỏi môn Văn”
Suy ra \(\overline A \) là biến cố “Học sinh được chọn không giỏi môn Toán”
\(\overline B \) là biến cố “Học sinh được chọn không giỏi môn Văn”.
Số học sinh giỏi cả hai môn là: 23 + 20 – 35 =8.
a) Trong 23 học sinh giỏi Toán, chỉ có đúng 8 học sinh giỏi văn nên xác suất để học sinh được chọn giỏi môn Toán biết rằng học sinh đó giỏi môn Văn là
P(A | B) = \(\frac{8}{{20}} = \frac{2}{5}.\)
Do đó, ý a đúng.
b) Trong số 20 học sinh giỏi Văn, có đúng 8 học sinh giỏi Toán nên xác suất để học sinh được chọn giỏi môn Văn biết rằng học sinh đó cũng giỏi môn Toán là
P(B | A) = \(\frac{8}{{23}}.\)
Do đó, ý b đúng.
c) Trong số 20 học sinh giỏi Văn, có đúng 8 học sinh giỏi cả Văn và Toán, nên số học sinh giỏi Văn mà không giỏi Toán là 12.
Xác suất để học sinh được chọn “không giỏi môn Toán biết rằng học sinh đó giỏi môn Văn” là: P(\(\overline A \) | B) = \(\frac{{12}}{{20}} = \frac{3}{5}.\)
Do đó, ý c sai.
d) Trong số 23 học sinh giỏi Toán, có đúng 8 học sinh giỏi cả Toán và Văn nên số học sinh không giỏi Văn mà giỏi Toán là 23 – 8 = 15.
Xác suất để học sinh được chọn “không giỏi môn Văn biết rằng học sinh đó giỏi môn Toán” là P(\(\overline B \) | A) = \(\frac{{15}}{{23}}.\)
Do đó, y d sai.
Câu 18:
Một công ty truyền thông đấu thầu 2 dự án. Khả năng thắng thầu của dự án 1 là 0,5 và dự án 2 là 0,6. Khả năng thắng thầu của 2 dự án là 0,4. Gọi \(A,B\) lần lượt là biến cố thắng thầu của dự án 1 và dự án 2.
a) \(A\) và \(B\) là hai biến cố độc lập.
b) Xác suất công ty thắng thầu đúng 1 dự án là 0,3.
c) Biết công ty thắng thầu dự án 1, xác suất để công ty thắng thầu dự án 2 là 0,4.
d) Biết công ty không thắng thầu dự án 2, xác suất để công ty thắng thầu dự án là 0,8.
Số mệnh đề sai trong các mệnh đề trên là:
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
a) Theo đề, ta có: P(A) = 0,5\( \Rightarrow P\left( {\overline A } \right) = 0,5\); P(B) = 0,6 \( \Rightarrow P\left( {\overline B } \right) = 0,4\);
P(A ∩ B) = 0,4.
Nhận thấy 0,4 ≠ 0,5.0,6 hay P(A∩B) ≠ P(A).P(B).
Do đó nên A và B là hai biến cố không độc lập.
b) Gọi C là biến cố “thắng thầu đúng 1 dự án”.
\(P\left( C \right) = P\left( {A \cap \overline B } \right) + P\left( {\overline A \cap B} \right)\)
\( = P\left( A \right) - P\left( {A \cap B} \right) + P\left( B \right) - P\left( {A \cap B} \right)\)
\( = P\left( A \right) + P\left( B \right) - 2P\left( {A \cap B} \right)\)
= 0,5 + 0,6 – 2.0,4 = 0,3.
Do đó, ý b đúng.
c) Gọi D là biến cố “thắng dự án 2 biết thắng dự án 1”.
P(D) = P(B | A) = \(\frac{{P\left( {B \cap A} \right)}}{{P\left( A \right)}} = \frac{{0,4}}{{0,5}} = 0,8.\)
Do đó, ý c là sai.
d) Gọi E là biến cố “thắng dự án 2 biết không thắng dự án 1”.
P(E) = \(P\left( {B|\overline A } \right) = \frac{{P\left( {B \cap \overline A } \right)}}{{P\left( {\overline A } \right)}} = \frac{{P\left( B \right) - P\left( {A \cap B} \right)}}{{P\left( {\overline A } \right)}} = \frac{{0,6 - 0,4}}{{0,5}} = 0,4.\)
Do đó, ý d sai.
Câu 19:
Hộp thứ nhất có 4 viên bi xanh và 6 viên bi đỏ. Hộp thứ hai có 5 viên bi xanh và 4 viên bi đỏ. Các viên bi có cùng kích thước và khối lượng. Lấy ra ngẫu nhiên 1 viên bi từ hộp thứ nhất chuyển sang hộp thứ hai. Sau đó lại lấy ra ngẫu nhiên một viên bi từ hộp thứ hai. Tính xác suất của biến cố C: “Hai viên bi lấy ra khác màu”.
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
Gọi A là biến cố “Viên bi lấy ra từ hộp thứ nhất có màu xanh”.
Gọi B là biến cố “Viên bi lấy ra từ hộp thứ hai có màu đỏ”.
Ta có: P(A) = \(\frac{4}{{10}} = 0,4\); \(P\left( {\overline A } \right) = 1 - P\left( A \right) = 1 - 0,4 = 0,6.\)
P(B | A) = \(\frac{4}{{10}} = 0,4\); \(P\left( {\overline B |A} \right) = 1 - P\left( {B|A} \right) = 1 - 0,4 = 0,6.\)
\(P\left( {B|\overline A } \right) = 1 - P\left( {\overline B |\overline A } \right) = 1 - P\left( {B|\overline A } \right) = 1 - 0,5 = 0,5.\)
Ta có sơ đồ cây:
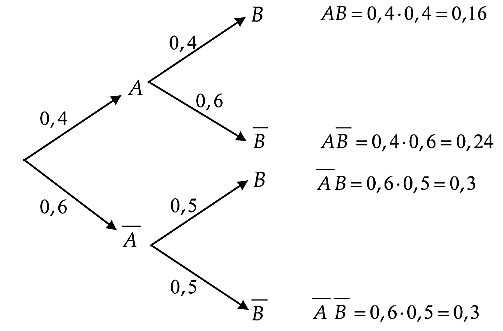
Dựa vào sơ đồ cây, ta có: P(C) = P(AB) + P(A ∩ B) = 0,16 + 0,3 = 0,46.
Câu 20:
Trong một túi có một số viên kẹo cùng loại, chỉ khác màu, trong đó có 6 viên kẹo màu cam, còn lại là kẹo màu vàng. Hà lấy ngẫu nhiên 1 viên kéo trong túi, không trả lại. Sau đó, Hà lại lấy ngẫu nhiên thêm một viên kẹo khác từ trong túi. Biết rằng xác suất để Hà lấy được cả hai viên kẹo màu cam là \(\frac{1}{3}.\) Hỏi ban đầu trong túi có bao nhiêu viên kẹo?
 Xem đáp án
Xem đáp án
Đáp án đúng là: 10
Gọi A là biến cố “Hà lấy được viên kẹo màu cam ở lần thứ nhất”
B là biến cố “Hà lấy được viên kẹo màu cam ở lần thứ hai”.
Ta có: xác suất Hà lấy được cả hai viên kẹo màu cam là \(\frac{1}{3}\), suy ra P(AB) = \(\frac{1}{3}\).
Gọi n là số viên kẹo ban đầu trong túi \(\left( {n \in {N^ * },n \ne 1} \right).\)
P(A) = \(\frac{6}{n}\); P(B | A) = \(\frac{5}{{n - 1}}\).
Theo công thức nhân xác suất, ta có:
P(AB) = P(A).P(A | B)
\( \Leftrightarrow \frac{6}{n}.\frac{5}{{n - 1}} = \frac{{30}}{{{n^2} - n}} = \frac{1}{3}\).
\( \Leftrightarrow {n^2} - n = 90 \Leftrightarrow {n^2} - n - 90 = 0\)\( \Leftrightarrow \left[ \begin{array}{l}n = - 9\\n = 10.\end{array} \right.\)
Do \(n \in {N^ * }\) nên \(n = 10\) thỏa mãn.
Vậy ban đầu trong túi có 10 viên kẹo.
