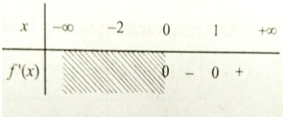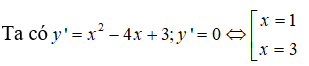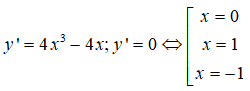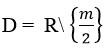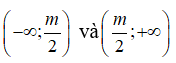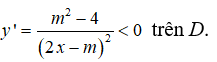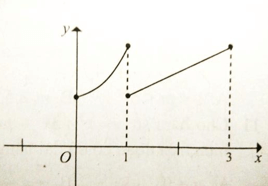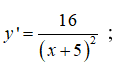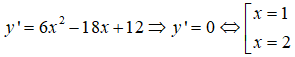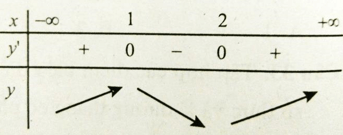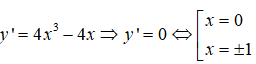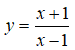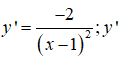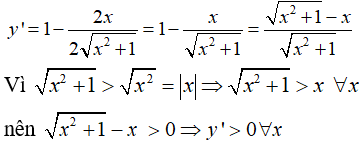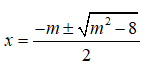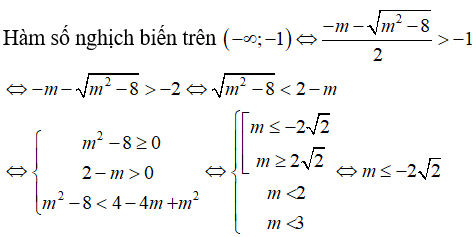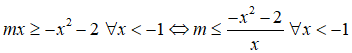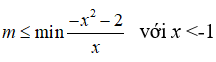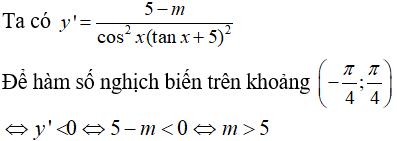21 câu trắc nghiệm: Sự đồng biến nghịch biến của hàm số có đáp án
-
10097 lượt thi
-
21 câu hỏi
-
50 phút
Danh sách câu hỏi
Câu 1:
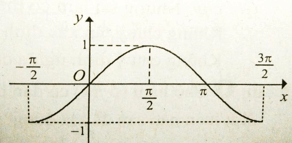
Cho đồ thị hàm số y = sin x với như hình vẽ.
Tìm khoảng đồng biến của hàm số y = sin x với
 Xem đáp án
Xem đáp án
Trên khoảng đồ thị hàm số đi lên từ trái sang phải.
Trên khoảng đồ thị hàm số đi xuống từ trái sang phải.
Do đó hàm số đồng biến trên khoảng
Chọn đáp án A.
Câu 2:
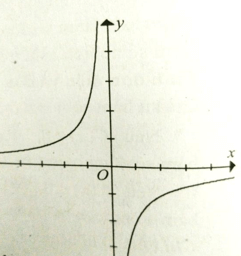
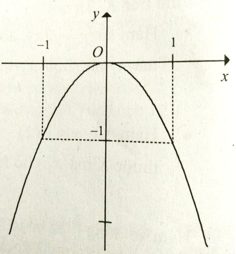
Cho đồ thị hàm số như hình vẽ. Hàm số nghịch biến trên khoảng:
 Xem đáp án
Xem đáp án
Trên khoảng (0; +∞) đồ thị hàm số đi xuống từ trái sang phải.
Do đó hàm số nghịch biến trên khoảng (0;+∞)
Chọn đáp án C.
Câu 3:
Cho đồ thị hàm số như hình vẽ. Hàm số đồng biến trên
 Xem đáp án
Xem đáp án
Đồ thị hàm số đi lên từ trái sang phải trên hai khoảng (-∞;0) và (0;+∞)
Chọn đáp án D.
Ghi chú. Những sai lầm có thể gặp trong quá trình làm bài:
- Không chú ý tập xác định nên chọn đáp án C.
- Không chú ý định nghĩa của hàm đồng biến nên chọn đáp án B.
Câu 4:
Cho hàm số f(x) có đạo hàm
Kết luận nào sau đây là đúng?
 Xem đáp án
Xem đáp án
Điều kiện: x > 0
Bảng xét dấu :
Vậy f(x) đồng biến trên khoảng (1;+∞) và nghịch biến trên khoảng (0;1).
Chọn đáp án D.
Câu 5:
Khoảng nghịch biến của hàm số là:
 Xem đáp án
Xem đáp án
TXĐ: D = R
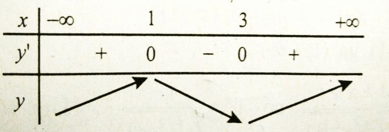
Bảng xét dấu y’ :
Vậy hàm số nghịch biến trên khoảng (1;3).
Chọn đáp án A.
Câu 6:
Cho hàm số . Kết luận nào sau đây đúng?
 Xem đáp án
Xem đáp án
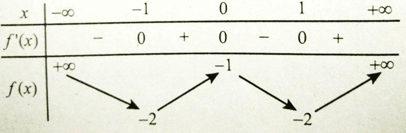
Bảng xét dấu y’:
Từ đó ta có: Hàm số đồng biến trên các khoảng (-1; 0) và (1; +∞) , nghịch biến trên các khoảng (-∞; -1) và (0; 1) . Chọn đáp án D.
Câu 7:
Cho hàm số y = sin2x - 2x. Hàm số này
 Xem đáp án
Xem đáp án
Tập xác định D = R
Ta có : y' = 2.cos2x - 2 = 2(cos2x - 1) ≤ 0; ∀ x
(vì -1 ≤ cos2x ≤ 1)
Vậy hàm số luôn nghịch biến trên R
Chọn đáp án D.
Câu 9:
Tìm m để hàm số luôn nghịch biến trên khoảng xác định.
 Xem đáp án
Xem đáp án
Tập xác định
Hàm số nghịch biến trên từng khoảng
khi và chỉ khi
Suy ra hay -2 < m < 2. Chọn đáp án C.
Câu 10:
Cho hàm số , tìm tất cả các giá trị của tham số m để hàm số nghịch biến trên khoảng (0; +∞)
 Xem đáp án
Xem đáp án
Ta có . Hàm số nghịch biến trên khoảng (0; +∞) nếu y' ≤ 0 trên khoảng (o; +∞)
Cách 1: Dùng định lí dấu tam thức bậc hai.
Xét phương trình . Ta có Δ' = 9(1 + m)
TH1: Δ' ≤ 0 => m ≤ -1 khi đó, nên hàm số nghịch biến trên R .
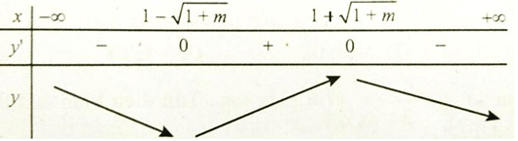
TH2: Δ' > 0 => m > -1; y' = 0 có hai nghiệm phân biệt là x = 1 ±√(1+m) .
Hàm số nghịch biến trên (0; +∞) <=> 1 + √(1+m) ≤ 0, vô lí.
Từ TH1 và TH2, ta có m ≤ -1
Cách 2: Dùng phương pháp biến thiên hàm số (cô lập tham số m).
Ta có: , ∀x > 0 <=>, ∀x > 0
Từ đó suy ra với x > 0
Mà
Suy ra: khi x= 1
Do đó 3m ≤ -3 hay m ≤ -1.
Chọn đáp án C.
Câu 11:
Cho đồ thị hàm số có dạng như hình vẽ.
Hàm số đồng biến trên:
 Xem đáp án
Xem đáp án
Chọn D
Trên khoảng (0; 1) đồ thị hàm số đi lên từ trái qua phải
Trên khoảng (1; 3) đồ thị hàm số đi lên từ trái qua phải
Đồ thị hàm số bị gián đoạn tại x = 1. Do đó hàm số đồng biến trên từng khoảng (0; 1) và (1; 3)
Câu 12:
Hỏi hàm số đồng biến trên khoảng nào?
 Xem đáp án
Xem đáp án
Chọn B
Hàm số xác định ∀x ≠ -5
y' xác định ∀x ≠ -5 và y' > 0
Vậy hàm số đồng biến trên các khoảng (-∞; -5) và (-5; +∞)
Câu 13:
Tìm khoảng đồng biến của hàm số
 Xem đáp án
Xem đáp án
Chọn B
Ta có
Bảng xét dấu đạo hàm:
Hàm số đồng biến trên các khoảng (-∞; 1) và (2; +∞)
Câu 14:
Khoảng nghịch biến của hàm số là:
 Xem đáp án
Xem đáp án
Chọn A
Ta có
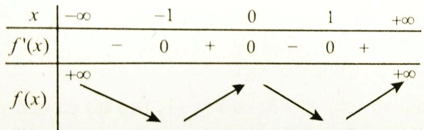
Bảng xét dấu đạo hàm
Hàm số nghịch biến trên các khoảng (-∞; -1) và (0; 1)
Câu 15:
Cho hàm số
Khẳng định nào sau đây là khẳng định đúng?
 Xem đáp án
Xem đáp án
Chọn B
Hàm số
xác định ∀x ≠ 1
Ta có:
xác định ∀x ≠ 1
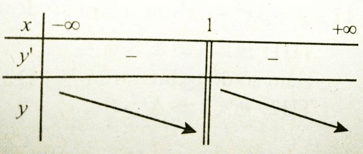
Bảng xét dấu đạo hàm
Hàm số nghịch biến trên các khoảng (-∞; 1) và (1; +∞)
Câu 18:
Cho hàm số Tìm điều kiện của tham số m để hàm số đồng biến trên R
 Xem đáp án
Xem đáp án
Chọn C
Hàm số đồng biến trên R ⇔ y' ≥ 0 ∀x ∈ R
Câu 19:
Cho hàm số
Tìm giá trị lớn nhất của tham số m để hàm số nghịch biến trên khoảng (-∞; -1).
 Xem đáp án
Xem đáp án
Chọn C
Ta có . Hàm số nghịch biến trên khoảng (-∞; - 1) nếu trên khoảng (-∞; -1)
Cách 1. Dùng định lí dấu của tam thức bậc hai. Ta có
TH1: => Δ ≤ 0.
Lại có, hệ số a= -1 < 0 nên y' ≤ 0 ∀ x
Hàm số nghịch biến trên R
TH2: 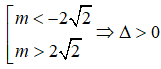
Từ TH1 và TH2, ta có
Cách 2. Dùng phương pháp biến thiên hàm số
Ta có
Từ đó suy ra
Do đó
Vậy giá trị lớn nhất của tham số m để hàm số nghịch biến trên khoảng (-∞; -1) là
Câu 21:
Cho hàm số Tìm các giá trị của m để hàm số đồng biến trên đoạn có độ dài bằng 1.
 Xem đáp án
Xem đáp án
. Hàm số đồng biến nếu y' ≥ 0. Ta có Δ' = 9 - 3m
TH1: m ≥ 3 => Δ' ≤ 0 .
Hàm số đồng biến trên R. Do đó m ≥ 3 không thỏa mãn yêu cầu đề bài
TH2: m < 3 => Δ' > 0 .
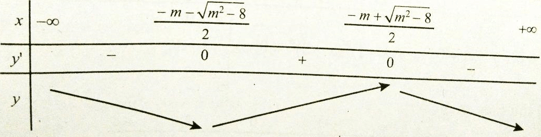
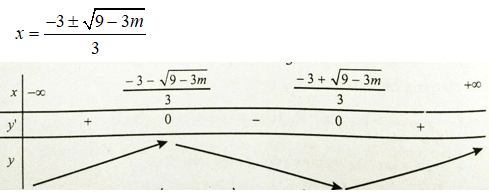
y’ có hai nghiệm phân biệt là
Từ bảng biến thiên, ta thấy không tồn tại m để hàm số đồng biến trên đoạn có độ dài bằng 1.
Từ TH1 và TH2, không tồn tại m thỏa mãn.
Chọn D