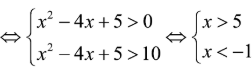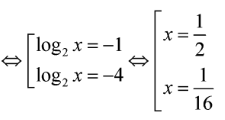256 Bài tập Hàm số mũ và Logarit cực hay có lời giải chi tiết (P5)
-
5797 lượt thi
-
53 câu hỏi
-
40 phút
Danh sách câu hỏi
Câu 1:
Đầu mỗi tháng chị Tâm gửi vào ngân hàng 3.000.000 đồng theo hình thức lãi kép với lãi suất là 0,6% một tháng. Biết rằng ngân hàng chỉ tất toán vào cuối tháng và lãi suất ngân hàng không thay đổi trong thời gian chị Tâm gửi tiền. Hỏi sau ít nhất bao nhiêu tháng kể từ khi bắt đầu gửi thì chị Tâm có được số tiền cả lãi và gốc không ít hơn 50.000.000 đồng ?
 Xem đáp án
Xem đáp án
Chọn A.
Phương pháp:
Sử dụng công thức lãi kép, số tiền gửi vào đầu hàng tháng trong đó:
M : số tiền gửi vào đều đặn đầu mỗi tháng.
r : lãi suất.
n : thời gian gửi.
A : số tiền nhận được sau n thời gian gửi.
Cách giải:
Giả sử sau n tháng người đó nhận được không ít hơn 50 000 000 đồng ta có:
![]()
![]()
![]()
Vậy sau ít nhất 16 tháng kể từ khi bắt đầu gửi thì chị Tâm có được số tiền cả lãi và gốc không ít hơn 50.000.000 đồng.
Câu 2:
Số nghiệm nguyên dương của bất phương trình là
 Xem đáp án
Xem đáp án
Chọn D.
Phương pháp:
Cách giải:
Vậy nghiệm nguyên dương của phương trình là
Câu 3:
Tìm tập xác định D của hàm số
 Xem đáp án
Xem đáp án
Chọn B.
Phương pháp:
Hàm số xác định
Cách giải:
Hàm số xác định
Vậy
Câu 4:
Gọi S là tập hợp tất cả các nghiệm nguyên dương của phương trình Số tập con của S bằng
 Xem đáp án
Xem đáp án
Chọn C.
Phương pháp:
Cách giải:
![]()
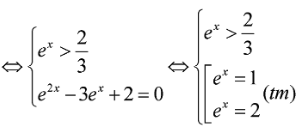
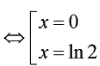
S là tập hợp tất cả các nghiệm nguyên dương của phương trình
Số tập con của S bằng 1, chính là tập hợp
Câu 5:
Biết rằng nếu thỏa mãn thì trong đó Tổng a+b bằng
 Xem đáp án
Xem đáp án
Chọn B.
Phương pháp:
+) Sử dụng công thức
tìm
+) Chặn khoảng giá trị của a , tìm thỏa mãn, từ đó tìm b và tính a + b.
Cách giải:
Theo đề bài ta có:
![]()
![]()
Ta có:
![]()
![]()
Vậy
Câu 6:
Với a là số thực dương bất kì, mệnh đề nào dưới đây đúng?
 Xem đáp án
Xem đáp án
Chọn C.
Phương pháp:
Sử dụng công thức
Cách giải:
Mệnh đề đúng là
Câu 7:
Tổng các nghiệm của phương trình trên đoạn [0;20] bằng
 Xem đáp án
Xem đáp án
Chọn C.
Cách giải:
ĐK:
Đặt
Ta có:
Xét hàm số
Hàm số đồng biến trên R.
Phương trình (*) có nhiều nhất 1 nghiệm
Ta thấy
nên là nghiệm duy nhất của (*)
![]()
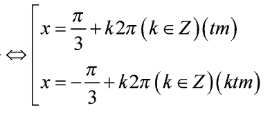
Mà
Tổng các nghiệm là
Câu 8:
Cho a,b là các số thực dương, a khác 1 . Khi đó bằng:
 Xem đáp án
Xem đáp án
Chọn C.
Phương pháp:
Sử dụng công thức:
Cách giải:
Câu 9:
Tổng tất cả các nghiệm của phương trình là:
 Xem đáp án
Xem đáp án
Chọn D.
Phương pháp:
Nhận xét nên đặt Sử dụng định lí Vi-ét.
Cách giải:
Ta có:
Đặt
Khi đó phương trình trở thành
Có Phương trình ẩn t có 2 nghiệm t1, t2 phân biệt
⇒ Phương trình ban đầu có 2 nghiệm x1, x2 phân biệt.
Ta có: ![]()
![]()
Câu 10:
Bất phương trình tương đương với bất phương trình nào sau đây?
 Xem đáp án
Xem đáp án
Chọn D.
Phương pháp:
Sử dụng phương pháp logarit 2 vế của bất phương trình
Cách giải:
![]()
![]()
Câu 11:
Tập nghiệm của phương trình là:
 Xem đáp án
Xem đáp án
Chọn B.
Phương pháp:
+)
+) Sử dụng công thức
Cách giải:
Vậy tập nghiệm của phương trình là
Câu 12:
Cho số thực a∈(0;1) . Đồ thị hàm số là hình vẽ nào dưới đây?
 Xem đáp án
Xem đáp án
Chọn C.
Phương pháp:
Dựa vào tính đồng biến, nghịch biến, TXĐ của các hàm số.
Cách giải:
Hàm số có TXĐ nên loại đáp án A và D.
Do a∈(0;1) nên hàm số nghịch biến trên (0;+∞).
Câu 13:
Áp suất không khí P (đo bằng milimet thủy ngân, kí hiệu là mmHg) suy giảm mũ so với độ cao x (so với mặt nước biển) (đo bằng mét) theo công thức trong đó là áp suất ở mực nước biển ( x = 0), i là hệ số suy giảm. Biết rằng ở độ cao 1000m thì áp suất của không khí là 672,71 mmHg . Hỏi áp suất không khí ở độ cao 3343m là bao nhiêu (làm tròn đến hàng phần trăm)?
 Xem đáp án
Xem đáp án
Chọn D.
Phương pháp:
+) Dựa vào dữ kiện ở độ cao 1000m thì áp suất của không khí là 672,71 mmHg tính i .
+) Tính áp suất không khí ở độ cao 3343m.
Cách giải:
Ở độ cao 1000m thì áp suất của không khí là 672,71 mmHg nên ta có:
Áp suất không khí ở độ cao 3343m là
Câu 15:
Cho số thực x thỏa mãn ( a,b,c là các số thực dương). Hãy biểu diễn x theo a, b, c.
 Xem đáp án
Xem đáp án
Phương pháp
Thu gọn vế trái, biến đổi đẳng thức về dạng
Cách giải:
Ta có:
Vậy
Chọn D.
Câu 16:
Một kĩ sư được nhận lương khởi điểm là 8.000.000 đồng/tháng. Cứ sau 2 năm lương mỗi tháng của kĩ sư đó được tăng thêm 10% so với mức lương hiện tại. Tính tổng số tiền T (đồng) kĩ sư đó nhận được sau 6 năm làm việc.
 Xem đáp án
Xem đáp án
Phương pháp
- Chia thành các giai đoạn 2 năm và tính lương nhận được của người đó trong khoảng thời gian đó.
- Cộng các kết quả ta được đáp án.
Cách giải:
+ Hai năm đầu : người đó nhận được triệu đồng.
+ Hai năm tiếp: người đó nhận được triệu đồng.
+ Hai năm cuối : người đó nhận được
triệu đồng.
Vậy sau 6 năm người đó đã nhận được 192 + 211,2 + 232,32 =635,52 triệu đồng hay 635.520.000 đồng.
Chọn A.
Câu 17:
Cho a số thực dương khác 1.
Tính
 Xem đáp án
Xem đáp án
Phương pháp:
Sử dụng công thức với
Cách giải:
Ta có:
Chọn A.
Câu 18:
Tập xác định của hàm số là
 Xem đáp án
Xem đáp án
Phương pháp:
Hàm số với không là số nguyên có điều kiện xác định
Cách giải:
Do Hàm số xác định
Suy ra TXĐ: D = (0;2).
Chọn B.
Câu 19:
Biết rằng phương trình có hai nghiệm thực Tích bằng
 Xem đáp án
Xem đáp án
Phương pháp
Sử dụng công thức
Đặt ẩn phụ rồi biến đổi để dử dụng hệ thức Vi-et.
Cách giải:
Ta có
Đặt ta có phương trình
Nhận thấy
Nên phương trình có hai nghiệm phân biệt t1; t2. Theo hệ thức Vi-ét ta có t1 + t2 = 1
Suy ra
Chọn D.
Chú ý: Phân biệt tích các nghiệm x, nhiều học sinh kết luận nhầm tích các nghiệm t.
Câu 20:
Biết bất phương trình có tập nghiệm là đoạn [a;b]. Tính b – a.
 Xem đáp án
Xem đáp án
Phương pháp:
Sử dụng phương pháp đưa về cùng cơ số và phương pháp giải bất phương trình
khi 0 < a < 1.
Cách giải:
Ta có:
Vậy tập nghiệm là đoạn
Chọn B.
Câu 21:
Anh A vào làm ở công ty X với mức lương ban đầu là 10 triệu đồng / tháng. Nếu hoàn thành tốt nhiệm vụ thì cứ sau 6 tháng làm việc, mức lương của anh lại được tăng thêm 20%. Hỏi bắt đầu từ tháng thứ mấy kể từ khi vào làm ở công ty X, tiền lương mỗi tháng của anh A nhiều hơn 20 triệu đồng ( biết rằng trong suốt thời gain làm ở công ty X anh A luôn hoàn thành nhiệm vụ)?
 Xem đáp án
Xem đáp án
Phương pháp:
Sử dụng công thức lãi kép với A là số tiền ban đầu, N là số kì hạn, r là lãi suất và T là số tiền có được sau N kì hạn.
Cách giải:
Gọi N là số lần tăng lương của anh A đến khi lương nhiều hơn 20 triệu. khi đó :
Vậy sau 4 lần tăng lương hay sau 4.6 = 24 tháng thì đến tháng thứ 25 anh A sẽ có mức lương trên 20 triệu.
Chọn B.
Câu 22:
Có bao nhiêu giá trị nguyên của tham số m để tập nghiệm của bất phương trình chứa đúng hai số nguyên?
 Xem đáp án
Xem đáp án
Phương pháp:
Sử dụng công thức với và với a > 1.
Đưa về dạng từ đó lập BBT và vẽ đồ thị của hàm số để tìm m.
Cách giải:
ĐK:
Ta có
![]()
![]()
![]()
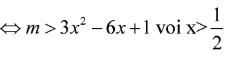
Xét hàm số với
Ta có
Đồ thị:
Quan sát đồ thị ta thấy, để bất phương trình có tập nghiệm chỉ chứa hai giá trị nguyên thì tập nghiệm của bất phương trình phải là với
Đường thẳng y = m phải cắt đồ thị hàm số tại duy nhất 1 điểm có hoành độ thỏa mãn
Vậy hay có 9 giá trị nguyên của m thỏa mãn bài toán.
Chọn D.
Câu 23:
Hàm số có tập xác định là D = R khi
 Xem đáp án
Xem đáp án
Cách giải:
ĐKXĐ:
Hàm số có tậ xác định là
Xét hàm số có
Bảng biến thiên:
Dựa vào BBT, ta có:
Chọn: C
Câu 24:
Tìm tập nghiệm S của phương trình
 Xem đáp án
Xem đáp án
Cách giải:
Ta có:
![]()
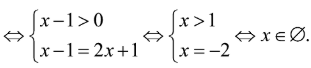
Tập nghiệm của phương trình đã cho là:
Chọn: B
Câu 25:
Với giá trị nào của x thì hàm số đạt giá trị lớn nhất?
 Xem đáp án
Xem đáp án
Cách giải:
đạt giá trị lớn nhất khi và chỉ khi đạt giá trị lớn nhất.
Ta có:
khi và chỉ khi
Vậy, hàm số đạt giá trị lớn nhất tại
Chọn: A
Câu 26:
Phương trình tiếp tuyến của đồ thị hàm số y=x ln x tại điểm có hoành độ bằng e là:
 Xem đáp án
Xem đáp án
Phương pháp:
Phương trình tiếp tuyến của đồ thị hàm số tại điểm là:
Cách giải:
Phương trình tiếp tuyến đó là:
Chọn D.
Câu 27:
Hỏi phương trình có tất cả bao nhiêu nghiệm thực?
 Xem đáp án
Xem đáp án
Phương pháp:
Chia cả hai vế cho
Sử dụng tính đơn điệu của hàm số để đánh giá nghiệm.
Cách giải:
Ta có: ![]()
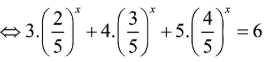 (*)
(*)
Nhận xét: nghịch biến trên R Phương trình (*) có nhiều nhất một nghiệm.
Mà và
Phương trình (*) có nghiệm thuộc khoảng (1;2) và là nghiệm duy nhất của phương trình (*).
Chọn: B
Câu 28:
Tập nghiệm của phương trình là:
 Xem đáp án
Xem đáp án
Phương pháp:
Đưa về phương trình logarit dạng:
Cách giải:
ĐKXĐ:
![]()
![]()
Vậy, tập nghiệm của phương trình là: S = {1}.
Chọn B.
Chú ý:
Chú ý điều kiện xác định của hàm số logarit.
Câu 29:
Cho a,b>0 , biểu thức bằng biểu thức nào sau đây?
 Xem đáp án
Xem đáp án
Phương pháp:
Sử dụng các công thức:
![]()
![]() (giả sử các biểu thức có nghĩa).
(giả sử các biểu thức có nghĩa).
Cách giải:
Chọn: D
Câu 30:
Phương trình có nghiệm nguyên dương là a.
Tính giá trị biểu thức
 Xem đáp án
Xem đáp án
Phương pháp:
Đưa về phương trình mũ.
Cách giải:
ĐKXĐ:
Ta có:
Nghiệm nguyên dương của phương trình là a = 3.
Chọn B.
Câu 33:
Đầu mỗi tháng, chị B gửi vào ngân hàng 3 triệu đồng theo hình thức lãi kép với lãi suất 0,6% một tháng và lãi suất không thay đổi suốt quá trình gửi tiền. Hỏi sau bao nhiêu tháng chị B có một số tiền cả gốc và lãi nhiều hơn 150 triệu đồng?
 Xem đáp án
Xem đáp án
Chọn B
Gọi số tiền người đó gửi hàng tháng là triệu
+ Đầu tháng 1: người đó có a.
Cuối tháng 1: người đó có:
+ Đầu tháng 2: người đó có:
Cuối tháng 2 người đó có:
+ Đầu tháng 3: người đó có:
Cuối tháng 3: người đó có
…
+ Đến cuối tháng thứ n người đó có:
Ta cần tính tổng:
Áp dụng công thức cấp số nhân với công bội là 1,06 ta được
Vậy sau 43 tháng người đó thu được số tiền thỏa mãn yêu cầu của bài toán
Câu 38:
Cho các số thực a. Giá trị của biểu thức bằng giá trị của biểu thức nào trong các biểu thức sau đây?
 Xem đáp án
Xem đáp án
Chọn A
Câu 40:
Số nghiệm của phương trình là
 Xem đáp án
Xem đáp án
Chọn đáp án B
Đk : x > -3
Đặt , phương trình đã cho trở thành
Dễ thấy hàm số nghịch biến trên và nên phương trình (1) có nghiệm duy nhất t = 1.
Với t = 1, ta có
Vậy phương trình có nghiệm duy nhất x = 2
Câu 41:
Cho a, b là các số dương tùy ý, khi đó ln (a + ab) bằng
 Xem đáp án
Xem đáp án
Phương pháp
Sử dụng công thức loga(bc) = loga b + loga c (0 < a ≠ 1; b, c > 0 )
Cách giải:
Ta có ln( a + ab ) = ln( a (1 + b )) = lna + ln(1 + b )
Chọn B.
Câu 42:
Bất phương trình có tập nghiệm là (a; b). Khi đó giá trị của b - a là
 Xem đáp án
Xem đáp án
Phương pháp
Đưa về giải bất phương trình có cơ số 0 < a < 1 :
Cách giải:
Ta có
Tập nghiệm của bất phương trình S = (-1; 3) ⇒ a = -1; b = 3 nên b - a = 4.
Chọn A.
Chú ý :
Một số em không đổi dấu bất phương trình dẫn đến không ra đáp án.
Câu 43:
Giá trị của biểu thức bằng
 Xem đáp án
Xem đáp án
Phương pháp
Sử dụng công thức
Cách giải:
Ta có
Chọn B.
Câu 44:
Tập xác định của hàm số là
 Xem đáp án
Xem đáp án
Phương pháp:
Hàm số xác định nếu f (x) xác định và f (x) > 0 .
Cách giải:
Hàm số xác định nếu
Vậy TXĐ : D = (-∞; 0) ∪ (2; +∞).
Chọn A.
Câu 45:
Tích tất cả các nghiệm của phương trình là
 Xem đáp án
Xem đáp án
Phương pháp:
Sử dụng với 0 < a ≠ 1; b > 0.
Sử dụng hệ thức Vi-ét để tính tích các nghiệm.
Cách giải:
Ta có
![]()
![]()
Nhận thấy nên phương trình có hai nghiệm phân biệt trái dấu x1; x2.
Theo hệ thức Vi-et ta có
![]()
Chọn C.
Câu 46:
Phương trình có hai nghiệm là a và a/b (với a,b ∈ N* và a/b là phân số tối giản). Giá trị của b là
 Xem đáp án
Xem đáp án
Phương pháp:
- Biến đổi phương trình về dạng f (u) = f (v) với u, v là các biểu thức ẩn x .
- Sử dụng phương pháp hàm đặc trưng, xét hàm y = f (t) suy ra mối quan hệ u, v.
Cách giải:
Điều kiện:
Khi đó ![]()
![]()
Xét hàm với t > 0 có
Do đó hàm số y = f(t) đồng biến trên (0; +∞).
Phương trình (*) là
Vậy phương trình có nghiệm 2 và nên a = 2, b = 3.
Chọn D.
Câu 47:
Cho phương trình . Tìm tất cả các giá trị nguyên của tham số m
để phương trình đã cho có hai nghiệm phân biệt x1 < x2 thỏa mãn x2 – 81x1 < 0
 Xem đáp án
Xem đáp án
Phương pháp:
+ Tìm ĐK.
+ Đặt từ đó đưa về phương trình bậc hai ẩn t.
+ Biến đổi yêu cầu bài toán để sử dụng được hệ thức Vi-ét.
Cách giải:
Đk: x > 0
Đặt ta có phương trình t2 - 4t + m - 3 = 0 (*)
Để phương trình đã cho có hai nghiệm phân biệt x1 < x2 thì phương trình (*) có hai nghiệm phân biệt
t1 < t2
Hay Δ' = 22 - (m - 3) = 7 - m > 0 ⇔ m < 7
Theo hệ thức Vi-et ta có
Ta có
Khi đó ![]()
![]()
Suy ra ![]()
![]()
Từ đó 3 < m < 7 mà m ∈ Z nên m ∈ {4; 5; 6}.
Vậy có 3 giá trị của m thỏa mãn đề bài.
Chọn C.
Câu 48:
Nghiệm của phương trình là
 Xem đáp án
Xem đáp án
Đáp án D.
? Cách 1:
Đk: nên loại phương án A và B.
Thay nghiệm ở hai phương án còn lại vào phương trình, nhận thấy nghiệm ở phương án D thỏa mãn. Vậy chọn D.
? Cách 2: Giải tự luận
Đk:
PT (tm(*)). Chọn D.
Câu 49:
Tổng tất cả các nghiệm của phương trình bằng
 Xem đáp án
Xem đáp án
Chọn B
TXĐ: .
.
Hàm số đồng biến trên
. (*)
Xét trên . Ta có
đồng biến trên
.
(*) .
Do m là số nguyên dương nên .
Câu 50:
Có bao nhiêu giá trị nguyên của tham số m để hàm số ) xác định với mọi x thuộc i?
 Xem đáp án
Xem đáp án
Chọn C
Điều kiện: .
Hàm số xác định trên
.
.
Kết hợp nên suy ra .
Vậy có 2020 số nguyên m thỏa yêu cầu bài toán.
Câu 51:
Một người thả một lượng bèo chiếm 2% diện tích mặt hồ. Giả sử tỉ lệ tăng trưởng của bèo hàng ngày là 20%. Hỏi sau ít nhất bao nhiêu ngày thì bèo phủ kín mặt hồ?
 Xem đáp án
Xem đáp án
Chọn A
Gọi S là diện tích mặt hồ Lượng bèo ban đầu trên mặt hồ sẽ là .
Sau n ngày thì lượng bèo tăng trưởng phủ kín mặt hồ nên
.
Vậy ít nhất 22 ngày thì bèo phủ kín mặt hồ.