30 câu hỏi trắc nghiệm thuộc Bài tập Cực trị hàm số cơ bản, nâng cao có lời giải (P3)

Câu 1:

Hàm số $y = x^{3} - 3 x + 1$ đạt cực đại tại $x$ bằng

A. 2

B. 1

C. 0

D. -1

Xem đáp án

Chọn D

Lập bảng biến thiên

$\Rightarrow$ Hàm số đạt cực đại tại x = -1

Câu 2:

Tìm giá trị cực đại $y_{C Đ}$ của hàm số $y = - x^{4} + 2 x^{2} - 5$

A. -4

B. -5

C. -2

D. -6

Xem đáp án

Chọn A

Lập bảng biến thiên . Suy ra $y_{C Đ} = - 4$

Câu 3:

Hàm số $y = \frac{1}{3} x^{3} - 2 x^{2} + 4 x - 1$ có bao nhiêu điểm cực trị?

A. 1

B. 0

C. 2

D. 3

Xem đáp án

Chọn B

Phương pháp tự luận

Hàm số không có cực trị

Câu 4:

Cho hàm số $y = x^{3} - 3 x^{2} + 2$ . Khẳng định nào sau đây đúng

A. Hàm số có cực đại, cực tiểu

B. Hàm số không có cực trị

C. Hàm số có cực đại , không có cực tiểu

D. Hàm số có cực tiểu không có cực đại

Xem đáp án

Chọn A

Phương pháp tự luận

Vậy hàm số đạt CĐ tại x = 0, CT tại x = 2.

Câu 5:

Cho hàm số $y = f (x)$ có bảng biến thiên như sau

Khi đó hàm số đã cho có

A. Một điểm cực đại, một điểm cực tiểu

B. Một điểm cực đại , hai điểm cực tiểu

C.1 điểm cực đại, không có điểm cực tiểu

D.2 điểm cực đại , 1 điểm cực tiểu

Xem đáp án

Chọn A

Câu 6:

Tìm tất cả các giá trị thực của $m$ để hàm số $y = m x^{4} - (m + 1) x^{2} + 2 m - 1$ có 3 điểm cực trị ?

B. m < -1

C. -1 < m <0

D. m > -1.

Xem đáp án

Chọn A

[Phương pháp tự luận]:

$y^{'} = 4 m x^{3} - 2 (m + 1) x = 0$

Hàm số có 3 điểm cực trị

[Phương pháp trắc nghiệm] :

Đồ thị hàm số $y = a x^{4} + b x^{2} + c$ có 3 cực trị khi và chỉ khi a và b trái dấu , tức là : ab < 0

Câu 7:

Tìm tất cả các giá trị thực của $m$ để hàm số $y = x^{3} - 2 x^{2} + (m + 3) x - 1$ không có cực trị?

A. $m \geq - \frac{8}{3}$ .

B. $m > - \frac{5}{3}$ .

C. $m \geq - \frac{5}{3}$ .

D. $m \leq - \frac{8}{3}$ .

Xem đáp án

Chọn C

[Phương pháp tự luận]

$y^{'} = 3 x^{2} - 4 x + m + 3$

Hàm số không có cực trị

Câu 8:

Tìm tất cả các giá trị thực của tham số $m$ để hàm số $y = \frac{1}{3} x^{3} - m x^{2} + (m + 1) x - 1$ đạt cực đại tại $x = - 2$ ?

A. Không tồn tại m

B. -1

C. 2

D. 3

Xem đáp án

Chọn A

Phương pháp tự luận

$\Leftrightarrow m = - 1$

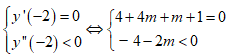
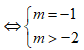
Câu 9:

Cho hàm số $y = f (x)$ liên tục trên R có bảng biến thiên

Trong các khẳng định sau, khẳng định nào là đúng?

A. Hàm số nghịch biến trên khoảng (1;3).

B. Hàm số đạt cực tiểu tại x = 3.

C. Hàm số có giá trị cực tiểu là $- \frac{1}{3}$

D. Hàm số không có cực trị

Xem đáp án

Chọn C

Câu 10:

Tìm tất cả các giá trị thực của tham số $m$ để hàm số $y = \frac{m}{3} x^{3} + 2 x^{2} + m x + 1$ có 2 điểm cực trị thỏa mãn $x_{C Đ} < x_{C T}$ .

A. m < 2

B. -2 < m < 0

C. -2 < m <2

D. 0 < m < 2.

Xem đáp án

Chọn D

[Phương pháp trắc nghiệm]

Để hàm số bậc 3 có 2 cực trị: $b^{2} - 3 a c > 0$

Để $x_{C Đ} < x_{C T} \Leftrightarrow a > 0$

Vậy ta có: $\{\begin{cases} 4 - m^{2} > 0 \\ \frac{m}{3} > 0 \end{cases} \Leftrightarrow 0 < m < 2$

Câu 11:

Tìm tất cả các giá trị thực của tham số m để hàm số: $y = \frac{1}{3} x^{3} + m x^{2} + (m + 6) x + m$ có cực đại và cực tiểu

A. -2 < m < 3

D. $- 2 \leq m \leq 3$ .

Xem đáp án

Chọn B

$y^{'} = x^{2} + 2 m x + m + 6$

Hàm số có cực đại và cực tiểu $\Leftrightarrow y^{'} = 0$ có hai nghiệm phân biệt

Câu 12:

Tìm tất các giá trị thực của tham số m để hàm số $y = (m + 2) x^{3} + 3 x^{2} + m x - 6$ có 2 cực trị ?

A. $m \in (- 3; 1) / \{- 2\}$ .

B. $m \in (- 3; 1)$ .

C. $m \in (- \infty; - 3) \cup (1; + \infty)$ .

D. $m \in [- 3; 1]$ .

Xem đáp án

Chọn A

Hàm số có 2 cực trị $\Leftrightarrow y^{'} = 0$ có hai nghiệm phân biệt.

Câu 13:

Tìm tất các giá trị thực của tham số m để hàm số $y = \frac{1}{3} x^{3} + (m + 3) x^{2} + 4 (m + 3) x + m^{3} - m$ đạt cực trị tại $x_{1}, x_{2}$ thỏa mãn $- 1 < x_{1} < x_{2}$

A. $- \frac{7}{2} < m < - 2$ .

B. $- 3 < m < 1$ .

D. $- \frac{7}{2} < m < - 3$ .

Xem đáp án

Chọn A

Hàm số có 2 cực trị $\Leftrightarrow y^{'} = 0$ có hai nghiệm phân biệt $x_{1}, x_{2}$ thỏa mãn: $- 1 < x_{1} < x_{2}$

Câu 14:

Tìm tất cả các giá trị thực của tham số m để hàm số $y = \frac{1}{3} x^{3} + (m^{2} - m + 2) x^{2} + (3 m^{2} + 1) x$ đạt cực tiểu tại $x = - 2$

B. $m = 3$ .

C. . $m = 1$

Xem đáp án

Chọn B

Hàm số đạt cực tiểu tại x = -2 khi

$\Leftrightarrow m = 3$

Câu 15:

Tìm các giá trị của tham số m để hàm số: $y = \frac{1}{3} m x^{3} - (m - 1) x^{2} + 3 (m - 2) x + \frac{1}{6}$ đạt cực trị tại $x_{1}, x_{2}$ thỏa mãn $x_{1} + 2 x_{2} = 1$

A. $1 - \frac{\sqrt{6}}{2} < m < 1 + \frac{\sqrt{6}}{2}$ .

C. $m \in (1 - \frac{\sqrt{6}}{2}; 1 + \frac{\sqrt{6}}{2}) \ \{0\}$ .

D. $m = 2$ .

Xem đáp án

Chọn B

$y^{'} = m x^{2} - 2 (m - 1) x + 3 (m - 2)$

Yêu cầu của bài toán $\Leftrightarrow y^{'} = 0$ có hai nghiệm phân biệt $x_{1}, x_{2}$ thỏa mãn: $x_{1} + 2 x_{2} = 1$

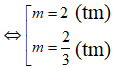
Câu 16:

Tìm các giá trị của tham số m để hàm số $y = m x^{4} + (m - 1) x^{2} + m$ chỉ có đúng một cực trị

A. $0 < m \leq 1$ .

D. $0 \leq m \leq 1$ .

Xem đáp án

Chọn C

Trường hợp 1: m = 0

Ta có hàm số: $y = - x^{2}$ , hàm số này có 1 cực trị.

Vậy m = 0 thỏa mãn.

Trường hợp 2: m ≠ 0

$y^{'} = 4 m x^{3} + 2 (m - 1) x$

Hàm số có đúng 1 cực trị.

Kết hợp TH1 và TH2

Câu 17:

Tìm các giá trị của tham số m để hàm số $y = m x^{4} + (m^{2} - 4 m + 3) x^{2} + 2 m - 1$ có ba điểm cực trị

A. $m \in (- \infty; 0)$ .

B. $m \in (0; 1) \cup (3; + \infty)$ .

C. $m \in (- \infty; 0) \cup (1; 3)$ .

D. $m \in (1; 3)$ .

Xem đáp án

Chọn C

Hàm số có 3 cực trị

Cách 2: Phương pháp trắc nghiệm

Với $m \neq 0$ hàm số là hàm trùng phương.

Hàm trùng phương có 3 cực trị $\Leftrightarrow a b < 0 \Leftrightarrow m (m - 1) (m - 3) < 0$

Lập bảng xét dấu ta được: $m \in (- \infty; 0) \cup (1; 3)$

Câu 18:

Tìm các giá trị của tham số m để đồ thị hàm số: $y = x^{4} - 2 m^{2} x^{2} + 1$ có ba điểm cực trị là ba đỉnh của một tam giác vuông cân

A. m = -1.

B. m ≠ 0.

C. m = 1.

D. $m = \pm 1$ .

Xem đáp án

Chọn D

Hàm số có 3 điểm cực trị $\Leftrightarrow m \neq 0$

Khi đó 3 điểm cực trị của đồ thị hàm số là

Do tính chất đối xứng, ta có $∆ A B C$ cân tại đỉnh A

Vậy $∆ A B C$ chỉ có thể vuông cân tại đỉnh A

Kết hợp điều kiện ta có: $m = \pm 1$ ( thỏa mãn).

Lưu ý: có thể sử dụng công thức $\frac{b^{3}}{8 a} + 1 = 0$ .

Câu 19:

Tìm các giá trị của tham số m để đồ thị hàm số: $y = x^{4} - 2 (m + 1) x^{2} + m^{2}$ có ba điểm cực trị là ba đỉnh của một tam giác vuông cân

A. Không tồn tại m

B. m = 0.

D. m = -1.

Xem đáp án

Chọn B

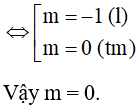
Câu 20:

Tìm các giá trị của tham số m để đồ thị hàm số: $y = x^{4} - 2 m x^{2} + 2 m + m^{4}$ có ba điểm cực trị là ba đỉnh của một tam giác đều

A. Không tồn tại m

C. $m = \sqrt[3]{3}$ .

D. $m = \pm \sqrt{3}$ .

Xem đáp án

Chọn C

Hàm số có 3 cực trị $\Leftrightarrow m > 0$

Khi đó 3 điểm cực trị của đồ thị hàm số là

Do tính chất đối xứng, ta có $∆ A B C$ cân tại đỉnh A

Vậy $∆ A B C$ đều chỉ cần AB = BC

Kết hợp điều kiện ta có $m = \sqrt[3]{3}$ (thỏa mãn)

Lưu ý: có thể sử dụng công thức $\frac{b^{3}}{8 a} + 3 = 0$

$\frac{{(- 2 m)}^{3}}{8} + 3 = 0 \Leftrightarrow m^{3} = 3 m \Leftrightarrow m = \sqrt[3]{3}$

Câu 21:

Khoảng cách giữa 2 điểm cực trị của đồ thị hàm số $y = x^{3} - 3 x$ là

A. $4 \sqrt{5}$

B. 2

C.2 $\sqrt{5}$

D. 4

Xem đáp án

Chọn C

Ta có: $y = x^{3} - 3 x$

$y' = 3 x^{2} - 3 = 0 \Leftrightarrow x = \pm 1$

Các điểm cực trị: $A (1; - 2); B (- 1; 2)$

Nên ta có $A B = 2 \sqrt{5}$

Câu 22:

Cho hàm số $y = \frac{1}{4} x^{4} - 2 x^{2} + 3$ có đồ thị là $(C)$ . Diện tích tam giác có các đỉnh là các điểm cực trị của đồ thị $(C)$ là:

A. m = 8.

B. m = 16

C. m = 32

D. m = 4

Xem đáp án

Chọn A

Ta có: $y = \frac{1}{4} x^{4} - 2 x^{2} + 3$

Các điểm cực trị: $A (- 2; - 1); B (0; 3); C (2; - 1)$

Các điểm cực trị tạo thành tam giác cân tại B $H (0; - 1)$ là trung điểm của AC

Nên $S_{∆ A B C} = \frac{1}{2} B H . A C = 8$

Câu 23:

Tìm tất cả các giá trị của tham số m để hàm số $y = \frac{1}{3} x^{3} - m x^{2} + (2 m - 1) x - 3$ có cực trị.

A. m ≠ 1.

B. $\forall m$

C. $m \leq 1$

D. $m \geq 1$

Xem đáp án

Chọn A

Câu 24:

Tìm tất cả các giá trị thực của tham số m để hàm số $y = m x^{4} + (m^{2} - 9) x^{2} + 10$ có 3 điểm cực trị

B. m < -3

C. $0 < m \leq 3$

Xem đáp án

Chọn A

Để hàm số có ba cực trị thì trước hết hàm số phải là hàm số trùng phương tức m ≠ 0

Ta có:

Hàm số có 3 cực trị khi và chỉ khi $y^{'}$ có 3 nghiệm phân biệt

$\Leftrightarrow \frac{m^{2} - 9}{2 m} < 0$

Vậy các giá trị cần tìm của m là m < - 3 hoặc 0 < m < 3.

Câu 25:

Tìm tất cả các giá trị thực của tham số m để hàm số $y = (m + 1) x^{4} - m x^{2} + \frac{3}{2}$ chỉ có cực tiểu mà không có cực đại

A. $m < - 1$

B. $- 1 < m \leq 0$

C. $m > 1$

D. $- 1 \leq m < 0$

Xem đáp án

Chọn B

Hàm trùng phương chỉ có 1 cực trị và cực trị đó là CT

$\Leftrightarrow \{\begin{cases} a > 0 \\ b \geq 0 \end{cases} \Leftrightarrow \{\begin{cases} m + 1 > 0 \\ - m \geq 0 \end{cases}$ $\Leftrightarrow - 1 < m \leq 0$

Câu 26:

Tìm tất cả các giá trị thực của tham số m để hàm số $y = x^{3} - 3 m x^{2} + (m - 1) x + 2$ có cực đại, cực tiểu và các điểm cực trị của đồ thị hàm số có hoành độ dương

A. $0 \leq m \leq 1$

B. $m \geq 1$

C. $m \geq 0$

D. $m > 1$

Xem đáp án

Chọn D

Ta có $y^{'} = 3 x^{2} - 6 m x + m - 1$

Hàm số có cực đại, cực tiểu khi và chỉ khi PT $y^{'} = 0$ có hai nghiệm phân biệt

Điều này tương đương

Hai điểm cực trị có hoành độ dương

Vậy các giá trị cần tìm của m là m >1

Câu 27:

Tìm tất cả các giá trị thực của tham số m để đồ thị của hàm số $y = - x^{3} + 3 m x + 1$ có 2 điểm cực trị A,B sao cho tam giác OAB vuông tại O( với O là gốc tọa độ ).

A. $m = \frac{3}{2}$

B. $m = - \frac{1}{3}$

C. $m = 1$

D. $m = \frac{1}{2}$

Xem đáp án

Chọn D

Ta có $y^{'} = - 3 x^{2} + 3 m$

$y^{'} = 0 \Leftrightarrow x^{2} - m = 0$ (*)

Đồ thị hàm số (1) có 2 điểm cực trị

$\Leftrightarrow P T (*)$ có 2 nghiệm phân biệt $\Leftrightarrow m > 0 (* *)$

Khi đó 2 điểm cực trị

Tam giác OAB vuông tại O

$V ậ y m = \frac{1}{2}$

Câu 28:

Tìm tất cả các giá trị của tham số m để đồ thị hàm số $y = x^{3} - 3 (m + 1) x^{2} + 12 m x - 3 m + 4 (C)$ có hai điểm cực trị là A và B sao cho hai điểm này cùng với điểm $C (- 1; - \frac{9}{2})$ lập thành tam giác nhận gốc tọa độ O làm trọng tâm

A. $m = \frac{1}{2}$

B. $m = - 2$

C. $m = 2$

D. $m = - \frac{1}{2}$

Xem đáp án

Chọn D

$T a c ó y^{'} = 3 x^{2} - 6 (m + 1) x + 12 m$

Hàm số có hai cực trị $\Leftrightarrow y^{'} = 0$ có hai nghiệm phân biệt

$\Leftrightarrow 9 m^{2} + 18 m + 9 - 36 m > 0$

$A (2; 9 m), B (2 m; - 4 m^{3} + 12 m^{2} - 3 m + 4)$

ABC nhận O làm trọng tâm

Câu 29:

Tìm tất cả các giá trị thực của tham số m để đồ thị hàm số $y = \frac{2}{3} x^{3} - m x^{2} - 2 (3 m^{2} - 1) x + \frac{2}{3}$ có hai điểm cực trị có hoành độ $x_{1}, x_{2}$ sao cho $x_{1} x_{2} + 2 (x_{1} + x_{2}) = 1$

A. $m = 0$

B. $m = - \frac{2}{3}$

C. $m = \frac{2}{3}$

D. $m = - \frac{1}{2}$

Xem đáp án

Chọn C

Ta có: $y^{'} = 2 x^{2} - 2 m x - 2 (3 m^{2} - 1)$

$g (x) = x^{2} - m x - 3 m^{2} + 1$ là tam thức bậc hai có $∆ = 13 m^{2} - 4$

Do đó hàm số có hai điểm cực trị khi và chỉ khi $y^{'}$ có hai nghiệm phân biệt

$\Leftrightarrow g (x)$ có hai nghiệm phân biệt

$x_{1}; x_{2}$ là các nghiệm của g(x) nên theo định lý Vi-ét, ta có

Đối chiếu với điều kiện (1), ta thấy chỉ $m = \frac{2}{3}$ thỏa mãn yêu cầu bài toán

Câu 30:

Gọi $x_{1}, x_{2}$ là hai điểm cực trị của hàm số $y = x^{3} - 3 m x^{2} + 3 (m^{2} - 1) x - m^{3} + m$ . Tìm tất cả các giá trị của tham số thực m để : ${x_{1}}^{2} + {x_{2}}^{2} - x_{1} x_{2} = 7$

A. $m = \pm \sqrt{2}$ .

B. $m = \pm 2$ .

C. $m = 0$ .

D. $m = \pm 1$ .

Xem đáp án

Chọn B

[Phương pháp tự luận]

$y^{'} = 3 x^{2} - 6 m x + 3 (m^{2} - 1)$

Hàm số luôn luôn có cực trị với moi m

Theo định lí Viet

$\{\begin{cases} x_{1} + x_{2} = 2 m \\ x_{1} . x_{2} = m^{2} - 1 \end{cases}$

${x_{1}}^{2} + {x_{2}}^{2} - x_{1} x_{2} = 7$

$\Leftrightarrow {(2 m)}^{2} - 3 (m^{2} - 1) = 7$

$\Leftrightarrow m = \pm 2$