19 câu hỏi trắc nghiệm thuộc Chuyên đề Toán 12 Bài 1: Khái niệm số phức có đáp án

Câu 1:

Phần ảo của số phức z = -7 + 6i bằng

A. -6

B. 6i

C. 6

D. -6i

Xem đáp án

Chọn C.

Phần ảo của số phức z là 6.

Câu 2:

Số phức có phần thực bằng 1 và phần ảo bằng 3 là

A. -1 - 3i

B. 1 + 3i

C. -1 + 3i

D. 1 - 3i

Xem đáp án

Chọn B.

Số phức có phần thực bằng 1 và phần ảo bằng 3 là z = 1 + 3i

Câu 3:

Cho số phức z = 3 - 2i. Tổng phần thực và phần ảo của số phức z bằng

A. 5

B. -1

C. -5

D. 1

Xem đáp án

Chọn D.

Số phức z = 3 - 2i có phần thực bằng 3 và phần ảo bằng -2

Vậy tổng phần thực và phần ảo của số phức z bằng 1

Câu 4:

Số phức liên hợp của số phức z = -1 + 3i là

A. 1 - 3i

B. 1 + 3i

C. -1 + 3i

D. -1 - 3i

Xem đáp án

Chọn D.

Số phức liên hợp của số phức

z = - 1 + 3 i

là

\bar{z} = - 1 - 3 i

Câu 5:

Cho số phức

\bar{z} = 3 + 4 i

. Phần thực và phần ảo của số phức z là

A. Phần thực là -4 và phần ảo là 3i

B. Phần thực 3 là và phần ảo là -4

C. Phần thực là -4 và phần ảo là 3

D. Phần thực là 3 và phần ảo là -4i

Xem đáp án

Chọn B.

Số phức

\bar{z} = 3 + 4 i

, suy ra số phức

z = \bar{z} = 3 - 4 i

có phần thực là 3 và phần ảo là -4

Câu 6:

Môđun của số phức z = 3 + 4i là

A. 7

B. 5

C. 3

D. $\sqrt{7}$

Xem đáp án

Chọn B.

Ta có $z = 3 + 4 i \Rightarrow |z| = \sqrt{3^{2} + 4^{2}} = 5$

Câu 7:

Cho số phức z = -12 + 5i. Môđun của số phức

\bar{z}

bằng

A. 13

B. 119

C. 17

D. -7

Xem đáp án

Chọn A.

Ta có: $|\bar{z}| = |z| = \sqrt{{(- 12)}^{2} + 5^{2}} = \sqrt{169} = 13$

Câu 8:

Trong mặt phẳng tọa độ Oxy, cho điểm M(-3,4) là điểm biểu diễn của số phức z. Môđun số phức z bằng

A. 1

B. 25

C. $\sqrt{7}$

D. 5

Xem đáp án

Chọn D.

Cách 1: Ta có: Điểm M(-3;4) là điểm biểu diễn của số phức z, nên z = -3 + 4i.

Suy ra, $|z| = \sqrt{{(- 3)}^{2} + 4^{2}} = 5$

Cách 2: Ta có

|z| = O M = \sqrt{{(- 3)}^{2} + 4^{2}} = 5

Câu 9:

Trong hình vẽ bên, điểm P biểu diễn số phức z₁, điểm Q biểu diễn số phức z₂ . Mệnh đề nào dưới đây đúng?

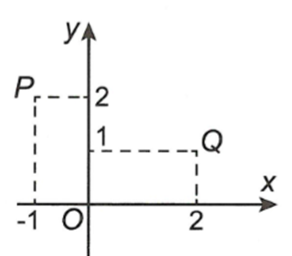
Trong hình vẽ bên, điểm P biểu diễn số phức z1, điểm Q biểu diễn số phức z2 . Mệnh đề nào dưới đây đúng? (ảnh 1)

A. $z_{1} = \bar{z_{2}}$

B. $|z_{1}| = |z_{2}| = 5$

C. $|z_{1}| = |z_{2}| = \sqrt{5}$

D. $z_{1} = - z_{2}$

Xem đáp án

Chọn C.

Ta có

z_{1} = - 1 + 2 i, z_{2} = 2 + i

\Rightarrow \{\begin{cases} |z_{1}| = \sqrt{{(- 1)}^{2} + 2^{2}} = \sqrt{5} \\ |z_{2}| = \sqrt{2^{2} + 1^{2}} = \sqrt{5} \end{cases} \Rightarrow |z_{1}| = |z_{2}| = \sqrt{5}

Câu 10:

Tìm các số thực x và y thỏa mãn điều kiện (2x + 1) + (3y - 2)i = (x + 2) + (y + 4)i

A. $\{\begin{cases} x = 1 \\ y = - 3 \end{cases}$

B. $\{\begin{cases} x = - 1 \\ y = 3 \end{cases}$

C. $\{\begin{cases} x = - 1 \\ y = - 3 \end{cases}$

D. $\{\begin{cases} x = 1 \\ y = 3 \end{cases}$

Xem đáp án

Chọn D.

Ta có $(2 x + 1) + (3 y - 2) i = (x + 2) + (y + 4) i \Leftrightarrow \{\begin{cases} 2 x + 1 = x + 2 \\ 3 y - 2 = y + 4 \end{cases} \Leftrightarrow \{\begin{cases} x = 1 \\ y = 3 \end{cases}$

Câu 11:

Biết rằng có duy nhất một cặp số thực (x;y) thỏa mãn (x + y) + (x - y)i = 5 + 3i. Giá trị của S = x + 2y là

A. S = 5

B. S = 4

C. S = 6

D. S = 3

Xem đáp án

Chọn C.

Ta có $(x + y) + (x - y) i = 5 + 3 i \Leftrightarrow \{\begin{cases} x + y = 5 \\ x - y = 3 \end{cases} \Leftrightarrow \{\begin{cases} x = 4 \\ y = 1 \end{cases}$

Vậy

S = x + 2 y = 6

Câu 12:

Có tất cả bao nhiêu cặp số thực (x;y) để hai số phức $z_{1} = 9 y^{2} - 4 - 10 x i^{5}, x_{2} = 8 y^{2} + 20 i^{11}$ là hai số phức liên hợp của nhau?

A. 1

B. 2

C. 3

D. 4

Xem đáp án

Chọn B.

Ta có

$z_{1} = \bar{z_{2}} \Leftrightarrow 9 y^{2} - 4 - 10 x i^{5} = 8 y^{2} - 20 i^{11} \Leftrightarrow 9 y^{2} - 4 - 10 x i = 8 y^{2} + 20 i$

$\Leftrightarrow \{\begin{cases} 9 y^{2} - 4 = 8 y^{2} \\ - 10 x = 20 \end{cases} \Leftrightarrow \{\begin{cases} x = - 2 \\ y = \pm 2 \end{cases}$

Vậy có hai cặp số thỏa mãn:

(- 2; - 2); (- 2; 2)

Câu 13:

Trong mặt phẳng Oxy, điểm nào sau đây biểu diễn số phức z = 2 + i?

A. M(2;0)

B. N(2;1)

C. P(2;-1)

D. Q(1;2)

Xem đáp án

Chọn B.

Điểm biểu diễn số phức z = 2 + 1 là N(2;1)

Câu 14:

Điểm nào trong hình vẽ dưới đây là điểm biểu diễn số phức z = -1 + 2i?

A. N

B. P

C. M

D. Q

Xem đáp án

Chọn D

Điểm biểu diễn cho số phức z = -1 + 2i là Q(-1;2)

Câu 15:

Cho z = -1 - 2i. Điểm nào trong hình vẽ bên là điểm biểu diễn số phức

\bar{z}

?

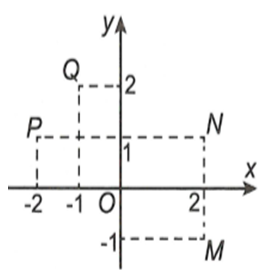
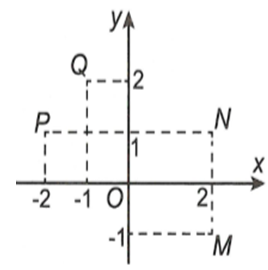
Cho z = -1 - 2i. Điểm nào trong hình vẽ bên là điểm biểu diễn số phức z (ảnh 1)

A. N

B. M

C. P

D. Q

Xem đáp án

Chọn D

Ta có

\bar{z} = - 1 + 2 i

nên điểm biểu diễn số phức

\bar{z}

là Q(-1;2)

Câu 16:

Cho hai điểm M, N trong mặt phẳng phức như hình bên. Gọi P là điểm sao cho OMPN là hình bình hành. Điểm P biểu thị cho số phức nào trong các số phức sau?

A. z = 4 - 3i

B. z = 4 + 3i

C. z = -2 + i

D. z = 2 - i

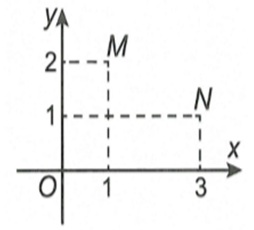
Xem đáp án

Chọn B

Cách 1: Giả sử $P (x; y)$ . Ta có: $\vec{M P} = (x - 1; y - 2); \vec{O N} = (3; 1) .$

Tứ giác OMPN là hình bình hành khi $\vec{M P} = \vec{O N} \Leftrightarrow \{\begin{cases} x - 1 = 3 \\ y - 2 = 1 \end{cases} \Leftrightarrow \{\begin{cases} x = 4 \\ y = 3 \end{cases} .$

Suy ra, P(4;3) là điểm biểu diễn số phức z = 4 + 3i

Cách 2: Ta có: $M (1; 2), N (3; 1) \Rightarrow I (2; \frac{3}{2})$ là trung điểm của đoạn thẳng MN

Tứ giác OMPN là hình bình hành nên I là trung điểm OP. Suy ra P(4;3), là điểm biểu diễn số phức z = 4 + 3i

Câu 17:

Các điểm A, B, C, D ở hình vẽ bên là các điểm biểu điểm biểu diễn cho các số phức

z_{1}, z_{2}, z_{3}, z_{4}

. Hỏi trong số đó có bao nhiêu số phức có môđun bằng 5

A. 1

B. 2

C. 3

D. 4

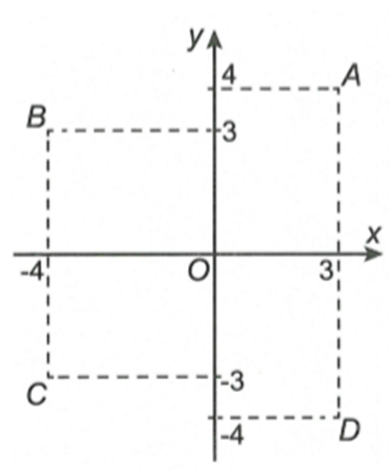
Xem đáp án

Chọn D

Ta có OA = OB = OC = OD = 5. Vậy, có bốn số phức có môđun bằng 5

Câu 18:

Gọi A, B, C lần lượt là các điểm biểu diễn của các số phức $z_{1} = 2,$ $z_{2} = 4 i,$ $z_{3} = 2 + 4 i$ trong mặt phẳng tọa độ Oxy. Diện tích tam giác ABC bằng

A. 8

B. 2

C. 6

D. 4

Xem đáp án

Chọn D.

Ta có $A (2; 0), B (0; 4), C (2; 4)$ suy ra $\vec{A C} = (0; 4); \vec{B C} = (2; 0) \Rightarrow \vec{A C} . \vec{B C} = 0.$

Do đó tam giác ABC là tam giác vuông tại C

Suy ra $S_{Δ A B C} = \frac{1}{2} C A . C B = \frac{1}{2} .4.2 = 4.$

Câu 19:

Tập hợp điểm biểu diễn các số phức z có phần ảo bằng 2 là

A. Đường thẳng có phương trình x = 2

B. Đường thẳng có phương trình x = -2

C. Đường thẳng có phương trình y = 2

D. Đường thẳng có phương trình y = -2

Xem đáp án

Chọn C.

Đặt $z = x + y i (x, y \in ℝ)$ . Số phức z có phần ảo bằng 2 khi y = 2

Vậy tập hợp điểm biểu diễn các số phức z có phần ảo bằng 2 là đường thẳng y = 2