Chuyên đề Toán 12 Bài 3: Ứng dụng của tích phân có đáp án
-
1116 lượt thi
-
23 câu hỏi
-
90 phút
Danh sách câu hỏi
Câu 1:
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Hoành độ giao điểm của \(\left( C \right)\) và trục hoành là nghiệm của phương trình:
\(\frac{{ - 3x - 1}}{{x - 1}} = 0 \Leftrightarrow x = - \frac{1}{3}\)
Do đó diện tích hình phẳng là
\(S = \left| {\int\limits_{ - \frac{1}{3}}^0 {\frac{{ - 3x - 1}}{{x - 1}}dx} } \right| = \left| {\int\limits_{ - \frac{1}{3}}^0 {\left( {3 + \frac{4}{{x - 1}}} \right)dx} } \right|\)
\( = \left( {3x + 4\ln \left| {x - 1} \right|} \right)\left| \begin{array}{l}^0\\_{ - \frac{1}{3}}\end{array} \right. = 4\ln \frac{4}{3} - 1\)
Câu 2:
 Xem đáp án
Xem đáp án
Ta có \(S = \int\limits_1^2 {\left| {{{\left( {x - 2} \right)}^2} - 1} \right|dx = } \int\limits_1^2 {\left| {{x^2} - 4x + 3} \right|dx} \)
Vì phương trình \({x^2} - 4x + 3\) không có nghiệm trên \(\left( {1;2} \right)\) nên \(S = \left| {\int\limits_1^2 {\left( {{x^2} - 4x + 3} \right)dx} } \right| = \frac{2}{3}\)
Chọn A.
Câu 3:
Gọi S là diện tích hình phẳng giới hạn bởi các đường \(y = f\left( x \right)\), trục hoành và hai đường thẳng \(x = - 3\), \(x = 2\) (như hình vẽ bên). Đặt \(a = \int\limits_{ - 3}^1 {f\left( x \right)dx} \), \(b = \int\limits_1^2 {f\left( x \right)dx} \).
Mệnh đề nào sau đây là đúng?
 Xem đáp án
Xem đáp án
Ta có \(S = \int\limits_{ - 3}^1 {\left| {f\left( x \right)} \right|dx} + \int\limits_1^2 {\left| {f\left( x \right)} \right|dx} = - \int\limits_{ - 3}^1 {f\left( x \right)dx} + \int\limits_1^2 {f\left( x \right)dx} = - a + b\)
Chọn D.
Câu 4:
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Ta có \(\ln x = 1 \Leftrightarrow x = e\).
Diện tích hình phẳng giới hạn bởi đồ thị các hàm số \(y = \ln x\), \(y = 1\) và đường thẳng \(x = 1\) là:
\(S = \int\limits_1^e {\left| {\ln x - 1} \right|dx} = \left| {\int\limits_1^e {\left( {\ln x - 1} \right)dx} } \right| = \left| {x\left( {\ln x - 1} \right)\left| \begin{array}{l}^e\\_1\end{array} \right. - \int\limits_1^e {dx} } \right| = \left| {1 - x\left| \begin{array}{l}^e\\_1\end{array} \right.} \right| = e - 2\)
Câu 5:
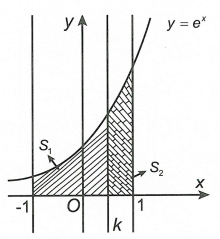
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Vì \({e^x} > 0\) với mọi \(x \in \mathbb{R}\) nên ta có
\({S_1} = \int\limits_{ - 1}^k {{e^x}dx} = {e^x}\left| \begin{array}{l}^k\\_{ - 1}\end{array} \right. = {e^k} - {e^{ - 1}}\) và \({S_2} = \int\limits_k^1 {{e^x}dx} = {e^x}\left| \begin{array}{l}^1\\_k\end{array} \right. = e - {e^k}\)
\({S_1} = {S_2} \Leftrightarrow {e^k} - {e^{ - 1}} = e - {e^k} \Leftrightarrow 2{e^k} = e + \frac{1}{e} \Leftrightarrow {e^k} = \frac{1}{2}\left( {e + \frac{1}{e}} \right)\)
\( \Leftrightarrow k = \ln \frac{1}{2}\left( {e + \frac{1}{e}} \right) = \ln \left( {e + \frac{1}{e}} \right) - \ln 2\)
Chọn C.
Chú ý: \({a^x} = b \Leftrightarrow x = {\log _a}b\)
Câu 6:
Cho hàm số \(y = f\left( x \right)\) có đồ thị trên \(\left[ { - 2;6} \right]\) như hình vẽ bên. Biết các miền A, B, \(x = 2\) có diện tích lần lượt là 32; 2; 3.
Tích phân \(\int\limits_{ - 2}^2 {\left[ {f\left( {2x + 2} \right) + 1} \right]dx} \) bằng
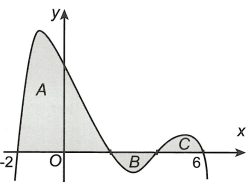
 Xem đáp án
Xem đáp án
Ta có \(\int\limits_{ - 2}^2 {\left[ {f\left( {2x + 2} \right) + 1} \right]dx} = \int\limits_{ - 2}^2 {f\left( {2x + 2} \right)dx} + 4\)
Xét \({I_1} = \int\limits_{ - 2}^2 {f\left( {2x + 2} \right)dx} \).
Đặt \(t = 2x + 2 \Rightarrow dt = 2dx \Rightarrow dx = \frac{{dt}}{2}\)
Đổi cận: \(x = - 2 \Rightarrow t = - 2\); \(x = 2 \Rightarrow t = 6\).
Suy ra \({I_1} = \frac{1}{2}\int\limits_{ - 2}^6 {f\left( t \right)dt} \).
Gọi \({x_1}\); \({x_2}\) là các hoành độ giao điểm của đồ thị hàm số \(y = f\left( x \right)\) với trực hoành \[\left( { - 2 < {x_1} < {x_2} < 6} \right)\] . Ta có
\[\begin{array}{l}{I_1} = \frac{1}{2}\left( {\int\limits_{ - 2}^{{x_1}} {f\left( t \right)df} + \int\limits_{{x_1}}^{{x_2}} {f\left( t \right)df} + \int\limits_{{x_2}}^6 {f\left( t \right)df} } \right) = \frac{1}{2}\left( {{S_A} - {S_B} + {S_C}} \right)\\ = \frac{1}{2}\left( {32 - 2 + 3} \right) = \frac{{33}}{2}\end{array}\]
Vậy \(\int\limits_{ - 2}^2 {\left[ {f\left( {2x + 2} \right) + 1} \right]dx} = {I_1} + 4 = \frac{{33}}{2} + 4 = \frac{{41}}{2}\)
Chọn D.
Câu 7:
Cho hàm số \(y = f\left( x \right)\) có đồ thị của hàm số \(y = f'\left( x \right)\) như hình bên.
Đặt \(g\left( x \right) = 2f\left( x \right) - {\left( {x + 1} \right)^2}\). Mệnh đề nào dưới đây đúng?
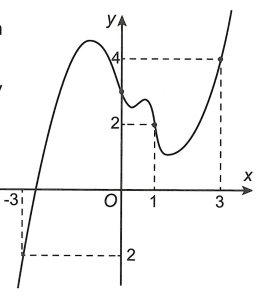
 Xem đáp án
Xem đáp án
Ta có \[g'\left( x \right) = 2f'\left( x \right) - 2\left( {x + 1} \right)\]
\[g'\left( x \right) = 0 \Leftrightarrow f'\left( x \right) = x + 1\]. Đây là phương trình hoành độ giao điểm của đồ thị hàm số \(f'\left( x \right)\) và đường thẳng d: \(y = x + 1\).
Dựa vào đồ thị ta thấy: \[g'\left( x \right) = 0 \Leftrightarrow f'\left( x \right) = x + 1 \Leftrightarrow \left[ \begin{array}{l}x = 1\\x = \pm 3\end{array} \right.\]
Bảng biến thiên:
|
x |
\( - \infty \) |
|
–3 |
|
1 |
|
3 |
|
\( + \infty \) |
|
\(g'\left( x \right)\) |
|
– |
0 |
+ |
0 |
– |
0 |
+ |
|
|
\(g\left( x \right)\) |
\( + \infty \) |

|
\(g\left( { - 3} \right)\) |
 |
\(g\left( 1 \right)\) |
 |
\(g\left( 3 \right)\) |
 |
\( + \infty \) |
Suy ra \(g\left( { - 3} \right) < g\left( 1 \right)\) và \(g\left( 3 \right) < g\left( 1 \right)\)
Gọi \({S_1}\), \({S_2}\) lần lượt là diện tích các hình phẳng giới hạn bởi đồ thị hàm số \(f'\left( x \right)\), đường thẳng d: \(y = x + 1\) trên các đoạn \(\left[ { - 3;1} \right]\) và \(\left[ {1;3} \right]\) ta có:
+) Trên đoạn \(\left[ { - 3;1} \right]\) ta có \(f'\left( x \right) \ge x + 1\) nên \({S_1} = \int\limits_{ - 3}^1 {\left| {g'\left( x \right)} \right|dx} = \frac{1}{2}\int\limits_{ - 3}^1 {\left[ {f'\left( x \right) - \left( {x + 1} \right)} \right]dx} \).
+) Trên đoạn \(\left[ {1;3} \right]\) ta có \(f'\left( x \right) \le x + 1\) nên \({S_2} = \int\limits_1^3 {\left| {g'\left( x \right)} \right|dx} = \frac{1}{2}\int\limits_1^3 {\left[ {\left( {x + 1} \right)f'\left( x \right)} \right]dx} \).
Dựa vào đồ thị ta thấy \({S_1} > {S_2}\) nên ta có:
\(g\left( x \right)\left| \begin{array}{l}^1\\_{ - 3}\end{array} \right. > - g\left( x \right)\left| \begin{array}{l}^3\\_1\end{array} \right. \Leftrightarrow g\left( 1 \right) - g\left( { - 3} \right) > - g\left( 3 \right) + g\left( 1 \right) \Leftrightarrow g\left( 3 \right) > g\left( { - 3} \right)\).
Vậy \(g\left( 1 \right) > g\left( 3 \right) > g\left( { - 3} \right)\).
Chọn D.
Câu 8:
Tính diện tích phần gạch chéo trên hình vẽ sau.
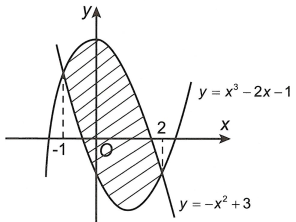
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Từ đồ thị ta thấy
\( - {x^2} + 3 \ge {x^2} - 2x - 1\) \(\forall x \in \left[ { - 1;2} \right]\)
Vậy diện tích phần hình phẳng gạch chéo trong hình vẽ là \(S = \int\limits_{ - 1}^2 {\left[ {\left( { - {x^2} + 3} \right) - \left( {{x^2} - 2x - 1} \right)} \right]dx} \)
\( = \int\limits_{ - 1}^2 {\left( { - 2{x^2} + 2x + 4} \right)dx} \)
\( = \left( {\frac{{ - 2}}{3}{x^3} + {x^2} + 4x} \right)\left| \begin{array}{l}^2\\_{ - 1}\end{array} \right.\)
\( = \frac{3}{2}\)Câu 9:
 Xem đáp án
Xem đáp án
Phương trình hoành độ giao điểm của hai đồ thị là
\({x^3} - 3x = x \Leftrightarrow {x^3} - 4x = 0 \Leftrightarrow \left[ \begin{array}{l}x = \pm 2\\x = 0\end{array} \right.\)
Vậy \(S = \left| {\int\limits_{ - 2}^0 {\left( {{x^3} - 4x} \right)dx} } \right| + \left| {\int\limits_0^2 {\left( {{x^3} - 4x} \right)dx} } \right| = 4 + 4 = 8\).
Chọn B.
Câu 10:
 Xem đáp án
Xem đáp án
Vì \(m > 0\) nên từ \(my = {x^2}\) ta suy \(y = \frac{{{x^2}}}{m} \ge 0\);
Từ \(mx = {y^2}\) nên \(x \ge 0\) và \(y = \sqrt {mx} \).
Xét phương trình \(\frac{{{x^2}}}{m} = \sqrt {mx} \Leftrightarrow {x^4} = {m^3}x \Leftrightarrow \left[ \begin{array}{l}x = 0\\x = m\end{array} \right.\)
Khi đó diện tích hình phẳng cần tìm là:
\(S = \int\limits_0^m {\left| {\sqrt {mx} - \frac{{{x^2}}}{m}} \right|dx} = \left| {\int\limits_0^m {\left( {\sqrt {mx} - \frac{{{x^2}}}{m}} \right)dx} } \right|\)
\( = \left| {\left( {\frac{{2\sqrt m }}{3}.x\sqrt x - \frac{{{x^3}}}{{3m}}} \right)\left| \begin{array}{l}^m\\_0\end{array} \right.} \right| = \left| {\frac{1}{3}{m^2}} \right| = \frac{1}{3}{m^2}\)
Yêu cầu bài toán \(S = 3 \Leftrightarrow \frac{1}{3}{m^2} = 3 \Leftrightarrow {m^2} = 9 \Leftrightarrow m = 3\) (vì \(m > 0\)).
Chọn C.
Câu 11:
Diện tích hình phẳng giới hạn bởi đồ thị của hai hàm \(y = {x^2}\) và \(y = \frac{{2x}}{{x - 1}}\) là \(S = a + b\ln 2\) với a, b là những số hữu tỷ. Giá trị của \(a + b\) là
 Xem đáp án
Xem đáp án
Phương trình hoành độ giao điểm của \(\left( {{C_1}} \right)\): \(y = {x^2}\) và \(\left( {{C_2}} \right)\): \(y = \frac{{2x}}{{x - 1}}\) là
\({x^2} = \frac{{2x}}{{x - 1}}\left( {x \ne 1} \right) \Rightarrow {x^3} - {x^2} - 2x = 0 \Leftrightarrow \left[ \begin{array}{l}x = 0\\x = - 1\\x = 2\end{array} \right.\)
Diện tích hình phẳng cần tìm là:
\(S = \int\limits_{ - 1}^0 {\left( {\frac{{2x}}{{x - 1}} - {x^2}} \right)dx} = \int\limits_{ - 1}^0 {\left( {2 + \frac{2}{{x - 1}} - {x^2}} \right)dx} = \left( {2x + 2\ln \left| {x - 1} \right| - \frac{{{x^3}}}{3}} \right)\left| \begin{array}{l}^0\\_{ - 1}\end{array} \right. = \frac{5}{3} - 2\ln 2\)
Suy ra \(a = \frac{5}{3}\) và \(b = - 2\)
Vậy \(a + b = - \frac{1}{3}\)
Chọn A.
Câu 12:
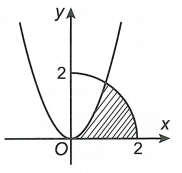
 Xem đáp án
Xem đáp án
Hướng dẫn giải
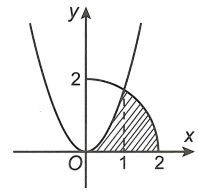
Phương trình hoành độ giao điểm của parabol \(y = \sqrt 3 {x^2}\) và cung tròn \(y = \sqrt {4 - {x^2}} \) (với \(0 \le x \le 2\)) lả \(\sqrt {4 - {x^2}} = \sqrt 3 {x^2} \Leftrightarrow 4 - {x^2} = 3{x^4} \Leftrightarrow x = 1\).
Diện tích của \(\left( H \right)\) là
\(S = \int\limits_0^1 {\sqrt 3 {x^2}dx} + \int\limits_1^2 {\sqrt {4 - {x^2}} dx} = \frac{{\sqrt 3 }}{3}{x^3}\left| \begin{array}{l}^1\\_0\end{array} \right. + I = \frac{{\sqrt 3 }}{3} + I\) với \(I = \int\limits_1^2 {\sqrt {4 - {x^2}} dx} \).
Đặt \(x = 2\sin t\), \(t \in \left[ { - \frac{\pi }{2};\frac{\pi }{2}} \right] \Rightarrow dx = 2\cos t.dt\)
Đổi cận \(x = 1 \Rightarrow t = \frac{\pi }{6}\), \(x = 2 \Rightarrow t = \frac{\pi }{2}\).
\(I = \int\limits_{\frac{\pi }{6}}^{\frac{\pi }{2}} {\sqrt {4 - 4{{\sin }^2}t} .2\cos t.dt} = \int\limits_{\frac{\pi }{6}}^{\frac{\pi }{2}} {4{{\cos }^2}t.dt} = \int\limits_{\frac{\pi }{6}}^{\frac{\pi }{2}} {2\left( {1 + \cos 2t} \right).dt} = \left( {2x + \sin 2t} \right)\left| \begin{array}{l}^{\frac{\pi }{2}}\\_{\frac{\pi }{6}}\end{array} \right.\)
\( = \frac{{2\pi }}{3} - \frac{{\sqrt 3 }}{2}\)
Vậy \(S = \frac{{\sqrt 3 }}{3} + I = \frac{{\sqrt 3 }}{3} + \frac{{2\pi }}{3} - \frac{{\sqrt 3 }}{2} = \frac{{4\pi - \sqrt 3 }}{6}\)
Chọn B.
Câu 13:
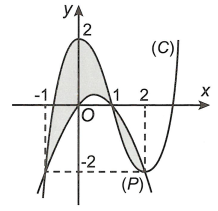
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Vì đồ thị hàm bậc ba và đồ thị hàm bậc hai cắt trục tung tại các điểm có tung độ lần lượt là \(y = 2\) và \(y = 0\) nên ta xét hai hàm số là \(y = a{x^3} + b{x^2} + cx + 2\), \(y = m{x^2} + nx\) (với a, \(m \ne 0\)).
Suy ra \(\left( C \right)\): \(y = f\left( x \right) = a{x^3} + b{x^2} + cx + 2\) và \(\left( P \right)\): \(y = g\left( x \right) = m{x^2} + nx\).
Phương trình hoành độ giao điểm của \(\left( C \right)\) và \(\left( P \right)\) là:
\(a{x^3} + b{x^2} + cx + 2 = m{x^2} + nx \Leftrightarrow \left( {a{x^3} + b{x^2} + cx + 2} \right) - \left( {m{x^2} + nx} \right) = 0\).
Đặt \(P\left( x \right) = \left( {a{x^3} + b{x^2} + cx + 2} \right) - \left( {m{x^2} + nx} \right)\).
Theo giả thiết, \(\left( C \right)\) và \(\left( P \right)\) cắt nhau tại các điểm có hoành độ lần lượt là \(x = - 1\), \(x = 1\), \(x = 2\) nên \(P\left( x \right) = a\left( {x + 1} \right)\left( {x - 1} \right)\left( {x - 2} \right)\).
Ta có \(P\left( 0 \right) = 2a\).
Mặt khác, ta có \(P\left( 0 \right) = f\left( 0 \right) - g\left( 0 \right) = 2 \Rightarrow a = 1\).
Vậy diện tích phần tô đậm là \(S = \int\limits_{ - 1}^2 {\left| {\left( {x + 1} \right)\left( {x - 1} \right)\left( {x - 2} \right)} \right|dx} = \frac{{37}}{{12}}\)
Chọn A.
Câu 14:
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Diện tích tam giác đều là \(S\left( x \right) = \frac{{\sqrt 3 {{\left( {2\sqrt {\cos 2x} } \right)}^2}}}{4} = \sqrt 3 \cos 2x\)
Thể tích vật thể là \(V = \int\limits_0^{\frac{\pi }{4}} {S\left( x \right)dx} = \int\limits_0^{\frac{\pi }{4}} {\sqrt 3 \cos 2xdx} = \frac{{\sqrt 3 }}{2}\sin 2x\left| \begin{array}{l}^{\frac{\pi }{4}}\\_0\end{array} \right. = \frac{{\sqrt 3 }}{2}\)
Chọn B.
Câu 15:
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Ta có \(V = \pi \int\limits_0^{\frac{\pi }{2}} {{y^2}dx} = \pi \int\limits_0^{\frac{\pi }{2}} {\left( {2 + \cos x} \right)dx} \)
\( = \pi \left( {2x + \sin x} \right)\left| \begin{array}{l}^{\frac{\pi }{2}}\\_0\end{array} \right. = \pi + \left( {\pi + 1} \right)\)
Câu 16:
 Xem đáp án
Xem đáp án
Thể tích của khối tròn xoay được tạo thành khi quay \(\left( H \right)\) được giới hạn bởi các đường \(y = {x^2} + 2\), \(y = 0\), \(x = 1\), \(x = 2\) xung quanh trục Ox là
\(V = \pi \int\limits_1^2 {{{\left( {{x^2} + 2} \right)}^2}dx} \)
Chọn C.
Câu 17:
 Xem đáp án
Xem đáp án
Thể tích của vật thể tròn xoay tạo thành khi hình phẳng \(\left( H \right)\) quay xung quanh trục Ox là
\(V = \pi \int\limits_1^2 {{{\left( {\frac{{\sqrt {2x - 1} }}{{2x + 1}}} \right)}^2}dx} = \pi \int\limits_1^2 {\frac{{2x - 1}}{{{{\left( {2x + 1} \right)}^2}}}dx} = \pi \int\limits_1^2 {\left[ {\frac{1}{{2x + 1}} - \frac{2}{{{{\left( {2x + 1} \right)}^2}}}} \right]dx} \)
\( = \pi \left( {\frac{1}{2}\ln \left( {2x + 1} \right) + \frac{1}{{2x + 1}}} \right)\left| \begin{array}{l}^2\\_1\end{array} \right. = \pi \left( {\frac{1}{2}\ln \frac{5}{3} - \frac{2}{{15}}} \right) = \pi \left( {\ln \frac{{\sqrt {15} }}{3} - \frac{2}{{15}}} \right)\)
Suy ra \(a = 15\), \(b = - \frac{2}{{15}}\)
Vậy \(a.b = - 2\).
Chọn D.
Câu 18:
 Xem đáp án
Xem đáp án
Hướng dẫn giải
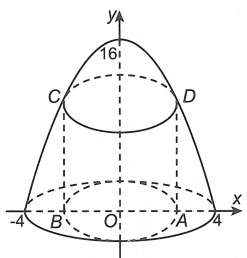
Ta có \(V = {V_y} = \pi \int\limits_0^{16} {\left( {16 - y} \right)dy} = 128\pi \)
Vì \(D \in \left( P \right)\) nên \(D\left( {a;16 - {a^2}} \right)\). Suy ra \(AD = 16 - {a^2}\).
Do đó khi xoay \(\left( {{H_1}} \right)\) quanh Oy ta được hình trụ tròn có bán kính \(R = a\) và chiều cao \(h = 16 - {a^2}\). Suy ra \({V_1} = \pi {a^2}\left( {16 - {a^2}} \right) = \pi \left( {16{a^2} - {a^4}} \right)\)
Xét hàm số \(f\left( x \right) = \pi \left( {16{a^2} - {a^4}} \right)\) trên \(\left[ {0;4} \right]\) ta thấy: \(f'\left( x \right) = \pi \left( {32x - 4{x^3}} \right)\)
\(f'\left( x \right) = 0 \Leftrightarrow \left[ \begin{array}{l}x = 0\\x = 2\sqrt 2 \\x = - 2\sqrt 2 \end{array} \right.\)
nên \(\mathop {\max }\limits_{\left[ {0;4} \right]} f\left( x \right) = f\left( {2\sqrt 2 } \right) = 64\pi \).
Vậy \(\max \left( {\frac{{{V_1}}}{V}} \right) = \frac{{64\pi }}{{128\pi }} = \frac{1}{2}\) khi \(a = 2\sqrt 2 \).
Chọn C.
Câu 19:
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Phương trình hoành độ giao điểm của đồ thị hàm số và trục hoành là \(2\left( {x - 1} \right){e^x} = 0 \Leftrightarrow x = 1\).
Thể tích của khối tròn xoay thu được khi quay hình \(\left( H \right)\) xung quanh trục Ox là:
\(V = \pi \int\limits_0^1 {{{\left[ {2\left( {x - 1} \right){e^x}} \right]}^2}dx} = 4\pi \int\limits_0^1 {{{\left( {x - 1} \right)}^2}{e^{2x}}dx} \)
Đặt \(\left\{ \begin{array}{l}u = {\left( {x - 1} \right)^2}\\dv = {e^{2x}}dx\end{array} \right. \Rightarrow \left\{ \begin{array}{l}du = 2\left( {x - 1} \right)dx\\v = \frac{{{e^{2x}}}}{2}\end{array} \right.\)
Suy ra \(V = 4\pi {\left( {x - 1} \right)^2}\frac{{{e^{2x}}}}{2}\left| \begin{array}{l}^1\\_0\end{array} \right. - 4\pi \int\limits_0^1 {\left( {x - 1} \right){e^{2x}}dx} = - 2\pi - 4\pi \int\limits_0^1 {\left( {x - 1} \right){e^{2x}}dx} \)
Gọi \({V_1} = 4\pi \int\limits_0^1 {\left( {x - 1} \right){e^{2x}}dx} \)
Đặt \(\left\{ \begin{array}{l}u = x - 1\\dv = {e^{2x}}dx\end{array} \right. \Rightarrow \left\{ \begin{array}{l}du = dx\\v = \frac{{{e^{2x}}}}{2}\end{array} \right.\)
Suy ra \({V_1} = 4\pi \left( {x - 1} \right)\frac{{{e^{2x}}}}{2}\left| \begin{array}{l}^1\\_0\end{array} \right. - 2\pi \int\limits_0^1 {{e^{2x}}dx} = 2\pi - \pi {e^{2x}}\left| \begin{array}{l}^1\\_0\end{array} \right. = 2\pi - \pi {e^2} + \pi = 3\pi - \pi {e^2}\)
\(V = - 2\pi - {V_1} = - 2\pi - \left( {3\pi - \pi {e^2}} \right) = \pi \left( {{e^2} - 5} \right)\)
Chọn D.
Câu 20:
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Tọa độ giao điểm của \(\left( {{C_1}} \right)\) và \(\left( {{C_2}} \right)\) là nghiệm của hệ phương trình
\(\left\{ \begin{array}{l}y = 2{x^2}\\{y^2} = 4x\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = y = 0\\x = 1;y = 2\end{array} \right.\)
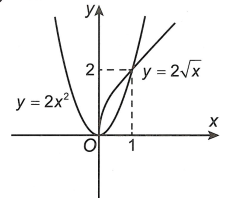
Với \(x \in \left[ {0;1} \right]\) thì \({y^2} = 4x \Leftrightarrow y = 2\sqrt x \) .
Vậy thể tích của khối tròn xoay cần tính là \(V = \pi \int\limits_0^1 {\left| {{{\left( {2{x^2}} \right)}^2} - {{\left( {2\sqrt x } \right)}^2}} \right|dx} \)
\( = \pi \int\limits_0^1 {\left( {4x - 4{x^2}} \right)dx} = \frac{{6\pi }}{5}\)
Chọn A.
Câu 21:
 Xem đáp án
Xem đáp án
Hướng dẫn giải
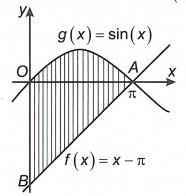
Xét phương trình hoành độ giao điểm của đồ thị các hàm số \(\left( {{C_1}} \right)\) và \(\left( {{C_2}} \right)\) là
\(x - \pi = \sin x \Leftrightarrow x - \pi - \sin x = 0\) \(\left( 1 \right)\).
Xét hàm số \(h\left( x \right) = x - \pi - \sin x \Rightarrow h'\left( x \right) = 1 - \cos x \ge 0\), \(\forall x \in \mathbb{R}\).
Suy ra \(h\left( x \right)\) đồng biến trên \(\mathbb{R}\) và \(x = \pi \) là một nghiệm của phương trình \(\left( 1 \right)\) nên \(x = \pi \) là nghiệm duy nhất của phương trình \(\left( 1 \right)\).
Do đó thể tích khối tròn xoay tạo thành khi quay \(\left( H \right)\) quanh trục hoành là thể tích của khối nón khỉ quay tam giác vuông OAB quanh trục hoành.
\(V = \frac{1}{3}.\pi .O{B^2}.OA = \frac{1}{3}.\pi .{\pi ^2}.\pi = \frac{1}{3}{\pi ^4} \Rightarrow p = \frac{1}{3}\)
Vậy \(24p = 24.\frac{1}{3} = 8\).
Chọn A.
Câu 22:
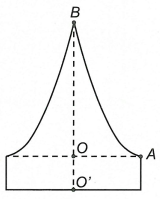
Để chuẩn bị cho đêm hội diễn văn nghệ chào đón năm mới, bạn An đã làm một chiếc mũ “cách điệu” cho ông già Noel có dáng một khối tròn xoay. Mặt cắt qua trục của chiếc mũ như hình vẽ bên. Biết rằng \(OO' = 5\,cm\), \(OA = 10\,cm\), \(OB = 20\,cm\), đường cong AB là một phần của parabol có đỉnh là điểm A. Thể tích của chiếc mũ bằng
 Xem đáp án
Xem đáp án
Ta gọi:
+) Thể tích của chiếc mũ là V.
+) Thể tích của khối trụ có bán kính đáy bằng \(OA = 10\,cm\)cm và đường cao \(OO' = 5\,cm\)là \({V_1}\).
+) Thể tích của vật thể tròn xoay khi quay hình phẳng giới hạn bởi đường cong AB và hai trục tọa độ quanh trục Oy là \({V_2}\).
Khi đó \({V_1} = {5.10^2}\pi = 500\pi \) và \(V = {V_1} + {V_2}\).
Chọn hệ trục tọa độ như hình vẽ.
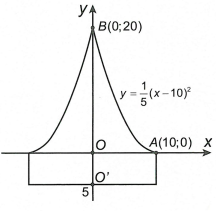
Do parabol có đỉnh A nên nó có phương trình dạng \(\left( P \right)\): \(y = a{\left( {x - 10} \right)^2}\).
Vì \(\left( P \right)\) qua điểm \(B\left( {0;20} \right)\) nên \(a = \frac{1}{5}\).
Do đó \(\left( P \right)\): \(y = \frac{1}{5}{\left( {x - 10} \right)^2}\). Từ đó suy ra \(x = 10 - \sqrt {5y} \)(do \(x < 10\) ).
Suy ra \({V_2} = \pi \int\limits_0^{20} {{{\left( {10 - \sqrt {5y} } \right)}^2}dy} = \pi \left( {3000 - \frac{{8000}}{3}} \right) = \frac{{1000}}{3}\pi \left( {c{m^3}} \right)\).
Vậy \(V = {V_1} + {V_2} = \frac{{1000}}{3}\pi + 500\pi = \frac{{2500}}{3}\pi \left( {c{m^3}} \right)\)
Chọn B.
Câu 23:
Gọi V là thể tích khối tròn xoay tạo thành khi quay hình phẳng giới hạn bởi các đường \(y = \sqrt x \), \(y = 0\) và \(x = 4\) quanh trục Ox. Đường thẳng \(x = a\)\(\left( {0 < a < 4} \right)\) cắt đồ thị hàm số \(y = \sqrt x \) tại M như hình vẽ bên dưới:

Gọi \({V_1}\) là thể tích khối tròn xoay tạo thành khi quay tam giác OMH quanh trục Ox. Biết rằng \(V = 2{V_1}\). Khi đó
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Ta có \(V = \pi \int\limits_0^4 {xdx} = \pi \frac{{{x^2}}}{2}\left| \begin{array}{l}^4\\_0\end{array} \right. = 8\pi \). Mà \(V = 2{V_1} \Rightarrow {V_1} = 4\pi \)
Gọi K là hình chiếu của M trên trục Ox.
Khi đó \(OK = a\), \(KH = 4 - a\), \(MK = \sqrt a \).
Khi xoay tam giác OMH quanh Ox ta được hai khối nón sinh bởi các tam giác OMK, MHK nên thể tích của khối tròn xoay đó là
\({V_1} = \frac{1}{3}.\pi .M{K^2}.OK + \frac{1}{3}.\pi .M{K^2}.KH = \frac{{4\pi a}}{3}\).
Từ \({V_1} = 4\pi \) suy ra \(\frac{{4\pi a}}{3} = 4\pi \Leftrightarrow a = 3\).
Chọn D.
