Trắc nghiệm Toán 12 Chân trời sáng tạo Bài 4. Khảo sát và vẽ đồ thị một số hàm số cơ bản có đáp án
Trắc nghiệm Toán 12 Chân trời sáng tạo Bài 4. Khảo sát và vẽ đồ thị một số hàm số cơ bản có đáp án
-
65 lượt thi
-
20 câu hỏi
-
60 phút
Danh sách câu hỏi
Câu 1:
I. Nhận biết
Đường cong trong hình bên là đồ thị của một hàm số trong bốn hàm số được liệt kê ở bốn phương án A, B, C, D dưới đây. Hỏi hàm số đó là hàm số nào?
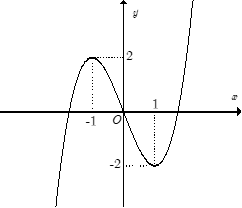
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
Đặc trưng của đồ thị là hàm bậc ba nên loại C, D.
Hình dáng đồ thị thể hiện a > 0 nên chỉ có A phù hợp.
Câu 2:
Đường cong trong hình vẽ bên là đồ thị hàm số nào dưới đây?
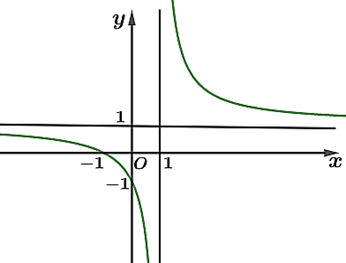
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Đồ thị đã cho là của hàm số nhất biến (bậc một trên bậc một) nên ta loại A, D.
Tiệm cận đứng của đồ thị là \(x = 1\), tiệm cận ngang của đồ thị là \(y = 1\). Loại B.
Câu 3:
Đường cong trong hình vẽ là đồ thị của hàm số nào dưới đây?
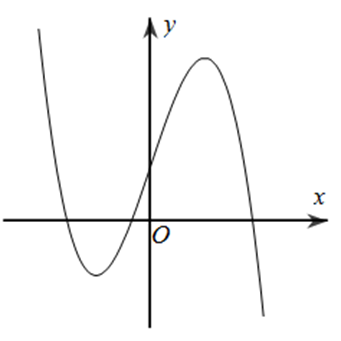
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
Đặc trưng của đồ thị là hàm bậc ba nên loại A, C.
Hình dáng đồ thị thể hiện a > 0 nên chỉ có B phù hợp.
Câu 4:
Tâm đối xứng của đồ thị hàm số \(y = {x^3} + 1\) là
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Tâm đối xứng của đồ thị hàm số là điểm có hoành độ là 0.
Thay x = 0 vào hàm số ta được y = 0.
Vậy tâm đối xứng của đồ thị hàm số là O(0; 0).
Câu 5:
Xác định tâm đối xứng của đồ thị hàm số sau
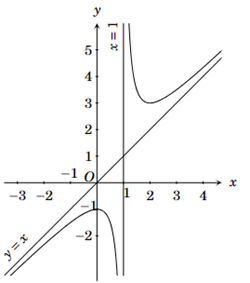
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
Đồ thị hàm số nhận \(B(1;\,\,1)\) giao điểm của hai đường tiệm cận làm tâm đối xứng.
Câu 6:
II. Thông hiểu
Cho hàm số y = f(x) = ax3 + bx2 + cx + d có bảng biến thiên sau:
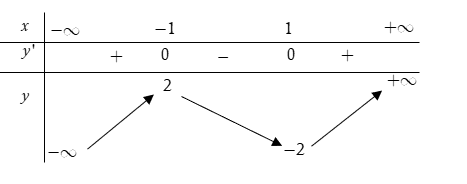
Đồ thị nào trong các phương án A, B, C, D thể hiện hàm số y = f(x)?
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: A
Dựa vào bảng biến thiên, ta thấy:
+) Khi x → +∞ thì y → +∞. Loại C và D.
+) Tọa độ các điểm cực trị là (−1; 2) và (1; −2) nên đáp án A là phù hợp.
Câu 7:
Trong bốn hàm số được liệt kê ở bốn phương án A, B, C, D dưới đây. Hàm số nào có bảng biến thiên như sau?
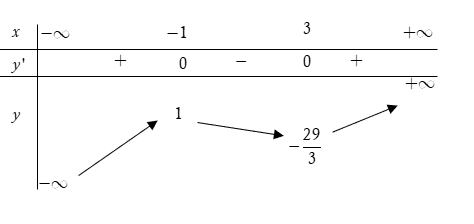
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
Dựa vào bảng biến thiên và các phương án lựa chọn, ta thấy:
Đây là dạng hàm số bậc 3 có hệ số a > 0. Loại A và D.
Mặt khác, đồ thị hàm số đi qua điểm (−1; 1) nên loại C.
Câu 8:
Biết rằng hàm số y = f(x) = ax3 + bx2 + cx + d (a ≠ 0) có đồ thị là một trong các dạng dưới đây:
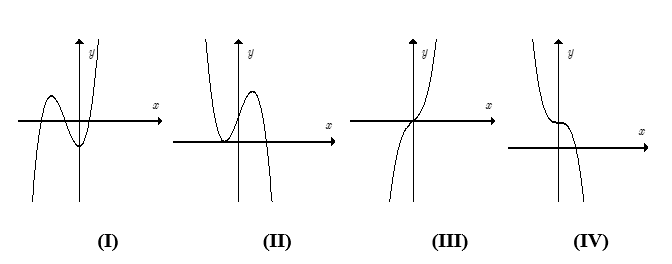
Mệnh đề nào sau đây là đúng?
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: C
Đồ thị (III) xảy ra khi a > 0 và f'(x) = 0 vô nghiệm hoặc có nghiệm kép.
Câu 9:
Bảng biến thiên trong hình dưới là đồ thị của một hàm số trong bốn hàm số được liệt kê ở bốn phương án A, B, C, D dưới đây. Hỏi hàm số đó là hàm số nào?
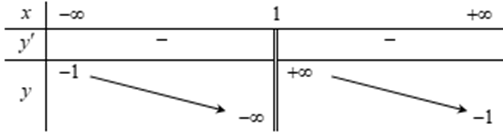
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Nhìn vào bảng biến thiên ta thấy ngay tiệm cận đứng \(x = 1\), tiệm cận ngang \(y = - 1\).
Suy ra loại đáp án A.
Nhìn vào bảng biến thiên, hàm số nghịch biến trên các khoảng \(\left( { - \infty ;1} \right)\) và \(\left( {1; + \infty } \right)\).
\(y = \frac{{ - x - 2}}{{x - 1}}\) có \(ad - bc = 3 > 0\). Loại đáp án B.
\(y = \frac{{ - x - 3}}{{x - 1}}\) có \(ad - bc = 4 > 0\). Loại đáp án D.
\(y = \frac{{ - x + 3}}{{x - 1}}\) có \(ad - bc = - 2 < 0\). </>
Chọn đáp án C.
Câu 10:
Hàm số \(y = \frac{{3x + 2}}{{x - 1}}\) có bảng biến thiên nào dưới đây. Chọn đáp án đúng?
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
Hàm số \(y = \frac{{3x + 2}}{{x - 1}}\) có tiệm cận đứng \(x = 1\) tiệm cận ngang \(y = 3\).
Câu 11:
Cho hàm số \[y = \frac{{ax - b}}{{x - 1}}\] có đồ thị như hình vẽ dưới đây:
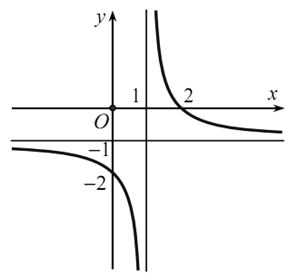
Khẳng định nào sau đây đúng?
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
Tiệm cận ngang của đồ thị hàm số là \[y = \frac{a}{1} = - 1 \Rightarrow a = - 1\].
Giao điểm của đồ thị hàm số với Oy là \(\left( {0\,;\,b} \right) \equiv \left( {0\,;\, - 2} \right) \Rightarrow b = - 2\).
Vậy \(b < a < 0\).
Câu 12:
Bảng biến thiên sau là của hàm số nào?
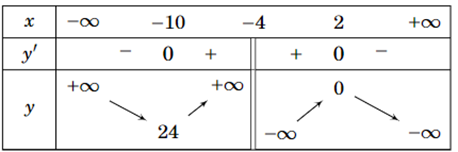
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
Dựa vào bảng biến thiên ta thấy đồ thị hàm số có tiệm cận đứng là x = −4.
Đồ thị hàm số đi qua hai điểm (−10; 24) và (2; 0) nên thay tọa độ 2 điểm vào các hàm số ta thấy đáp án B thỏa mãn.
Câu 13:
Bảng biến thiên sau là của đồ thị hàm số nào
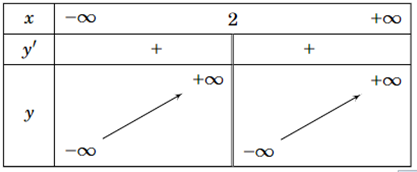
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
Dựa vào bảng biến thiên ta có đồ thị hàm số có tiệm cận đứng x = 2 và hàm số đồng biến trên khoảng (−∞; 2) và (2; +∞).
+) Xét hàm số\(y = \frac{{{x^2} - 3}}{{x - 2}}\) có \(y' = \frac{{2x\left( {x - 2} \right) - \left( {{x^2} - 3} \right)}}{{{{\left( {x - 2} \right)}^2}}} = \frac{{{x^2} - 4x + 3}}{{{{\left( {x - 2} \right)}^2}}}\). Loại.
+) Xét hàm số \(y = \frac{{{x^2} - 4x + 2}}{{x - 2}}\) có:
\(y' = \frac{{\left( {2x - 4} \right)\left( {x - 2} \right) - \left( {{x^2} - 4x + 2} \right)}}{{{{\left( {x - 2} \right)}^2}}} = \frac{{{x^2} - 4x + 6}}{{{{\left( {x - 2} \right)}^2}}} = \frac{{{{\left( {x - 2} \right)}^2} + 2}}{{{{\left( {x - 2} \right)}^2}}} > 0\). Chọn.
+) Xét hàm số \(y = \frac{{{x^2} - x}}{{x - 2}}\) có \(y' = \frac{{\left( {2x - 1} \right)\left( {x - 1} \right) - \left( {{x^2} - x} \right)}}{{{{\left( {x - 2} \right)}^2}}} = \frac{{{x^2} - 2x + 1}}{{{{\left( {x - 2} \right)}^2}}}\). Loại.
+) Xét hàm số \(y = \frac{{{x^2} - 4x + 5}}{{x - 2}}\) có:
\(y' = \frac{{\left( {2x - 4} \right)\left( {x - 2} \right) - \left( {{x^2} - 4x + 5} \right)}}{{{{\left( {x - 2} \right)}^2}}} = \frac{{{x^2} - 4x + 3}}{{{{\left( {x - 2} \right)}^2}}}\). Loại.
Câu 14:
Đồ thị hàm số ở hình sau là của hàm số nào
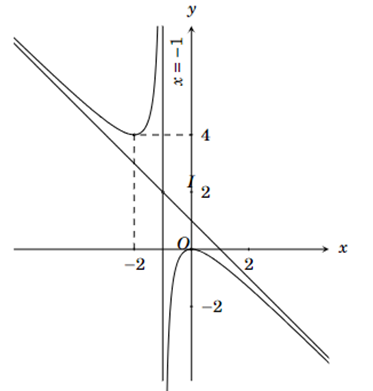
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
Dựa vào đồ thị hàm số ta thấy đồ thị hàm số có tiệm cận đứng x = −1 và đi qua O(0; 0) và (−2; 4).
Thay tọa độ O(0; 0) và (−2; 4) vào các hàm số ta thấy đáp án D thảo mãn.
Câu 15:
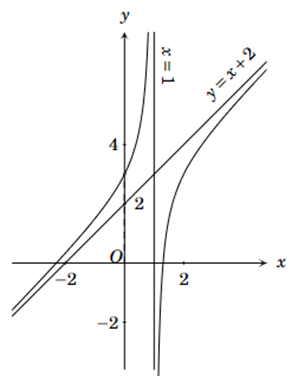
Đồ thị hàm số ở hình sau là của hàm số nào.
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
Dựa vào đồ thị hàm số ta thấy đồ thị hàm số có tiệm cận đứng là x = 1 và tiệm cận xiên là y = x + 2.
+) Xét hàm số \(y = \frac{{{x^2} + 3}}{{x - 1}} = x + 1 + \frac{4}{{x - 1}}\).
Đồ thị hàm số này có tiệm cận xiên là y = x + 1. Loại.
+) Xét hàm số \(y = \frac{{{x^2} + x - 3}}{{x - 1}} = x + 2 - \frac{1}{{x - 1}}\).
Đồ thị hàm số này nhận y = x + 2 làm tiệm cận xiên. Chọn.
+) Xét hàm số \(y = \frac{{{x^2} - 2x + 3}}{{ - x + 1}}\)\( = - x + 1 + \frac{2}{{ - x + 1}}\).
Đồ thị hàm số này nhận y = −x + 1 làm tiệm cận xiên. Loại.
+) Xét hàm số \(y = \frac{{{x^2} + 3}}{{ - x + 1}} = - x - 1 + \frac{4}{{ - x + 1}}\).
Đồ thị hàm số này nhận y = −x + 1 làm tiệm cận xiên. Loại.
Câu 16:
III. Vận dụng
Cho hàm số y = ax3 + bx2 + cx + d có đồ thị như hình vẽ bên dưới.
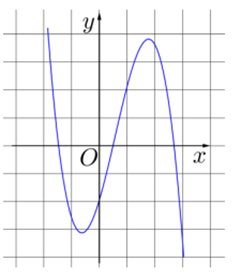
Mệnh đề nào dưới đây đúng?
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
Dựa vào dạng đồ thị ta có a < 0, d < 0.
Hàm số có hai điểm cực trị trái dấu nên a, c trái dấu suy ra c > 0.
Đồ thị hàm số có tâm đối xứng có hoành độ dương nên \( - \frac{b}{a} > 0 \Rightarrow b > 0\).
Câu 17:
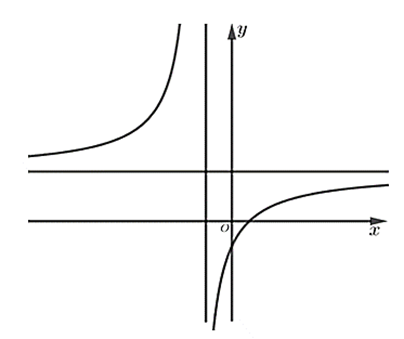
Cho hàm số \[y = \frac{{ax + b}}{{cx + d}}\] có đồ thị như trong hình bên dưới. Biết rằng \[a\] là số thực dương, hỏi trong các số \[b,\,\,c,\,\,d\] có tất cả bao nhiêu số dương?
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
Tiệm cận ngang của đồ thị nằm phía trên Ox nên \[y = \frac{a}{c} > 0\] mà \[a > 0 \Rightarrow c > 0\].
Tiệm cận đứng của đồ thị nằm bên trái Oy nên \[x = - \frac{d}{c} < 0 \Rightarrow \frac{d}{c} > 0\] mà \[c > 0 \Rightarrow d > 0\].
Giao điểm của đồ thị hàm số với Oy là \[\left( {0\,;\,\frac{b}{d}} \right)\] nằm dưới O nên \[\frac{b}{d} < 0\] mà \[d > 0 \Rightarrow b < 0\].
Vậy \[b < 0,\,\,c > 0,\,\,d > 0\].
Câu 18:
Trong một môi trường dinh dưỡng có 1000 vi khuẩn được cấy vào. Bằng thực nghiệm xác định được số lượng vi khuẩn tăng theo thời gian bởi qui luật \(N\left( t \right) = 1000 + \frac{{100t}}{{100 + {t^2}}}\) (con vi khuẩn), trong đó t là thời gian (đơn vị giây). Hãy xác định thời điểm sau khi thực hiện cấy vi khuẩn vào, số lượng vi khuẩn tăng lên lớn nhất là bao nhiêu?
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
Ta có tốc độ phát triển của đàn vi khuẩn tại thời điểm t là:
\(N'\left( t \right) = \frac{{{{100}^2} - 100{t^2}}}{{{{\left( {100 + {t^2}} \right)}^2}}}\left( {\forall t > 0} \right)\).
Xét N'(t) = 0 t2 = 100 t = 10 (vì t > 0).
Lập bảng biến thiên ta được
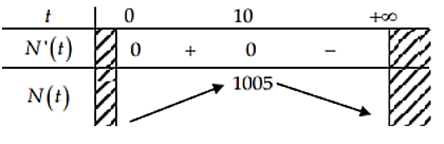
Dựa vào bảng biến thiên ta có maxN(t) = N(10) = 1005.
Câu 19:
Một người muốn xây một cái bể chứa nước, dạng một khối hộp chữ nhật không nắp có thể tích bằng \[288\,\,\,d{m^3}\]. Đáy bể là hình chữ nhật có chiều dài gấp đôi chiều rộng, giá thuê nhân công để xây bể là \[500\,000\] đồng/\({m^2}\). Nếu người đó biết xác định các kích thước của bể hợp lí thì chi phí thuê nhân công sẽ thấp nhất. Hỏi người đó trả chi phí thấp nhất để thuê nhân công xây dựng bể đó là bao nhiêu?
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
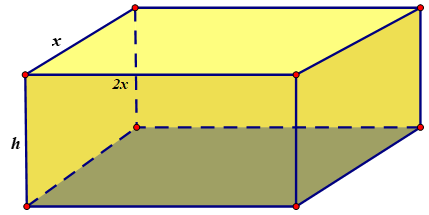
Gọi \(x\) chiều rộng của đáy bể \((x > 0)\).
Khi đó chiều dài của bể là \(2x.\)
Thể tích của bể: \(V = 288\,\,\,d{m^3} = 0,288\,\,\,{m^3}\) ,
mà \(V = x.2x.h \Rightarrow h = \frac{V}{{2{x^2}}} = \frac{{0,288}}{{2{x^2}}} = \frac{{0,144}}{{{x^2}}}\) .
Phần xây dựng của bể (trừ mặt trên của bể) có diện tích:
\(S = 2.hx + 2.h.2x + x.2x = 6hx + 2{x^2} = 6.\frac{{0,144}}{{{x^2}}}.x + 2{x^2} = \frac{{0,864}}{x} + 2{x^2}\).
Xét hàm số \(S(x) = \frac{{0,864}}{x} + 2{x^2}\,\,\,,x > 0.\)
Đạo hàm: \(y' = - \frac{{0,864}}{{{x^2}}} + 4x = \frac{{4{x^3} - 0,864}}{{{x^2}}};\,\,\,y' = 0 \Leftrightarrow 4{x^3} - 0,864 = 0 \Leftrightarrow x = \frac{3}{5} = 0,6\,\,\,m.\)
Bảng biến thiên:
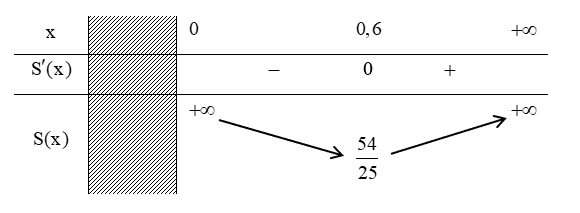
Vậy \({S_{Min}} = \frac{{54}}{{25}}\,\,\,{m^2} \Rightarrow \) Chi phí thấp nhất phải trả: \(\frac{{54}}{{25}}.500\,\,000 = 1\,\,080\,\,000\) đồng.
Câu 20:
Một tấm kẽm hình vuông \(ABCD\) có cạnh bằng \(30{\rm{ (cm)}}{\rm{.}}\) Người ta gập tấm kẽm theo hai cạnh \[EF\] và \(GH\) cho đến khi \(AD\) và \(BC\) trùng nhau như hình vẽ dưới đây để được một hình lăng trụ khuyết hai đáy. Giá trị của \(x\) để thể tích khối lăng trụ lớn nhất là
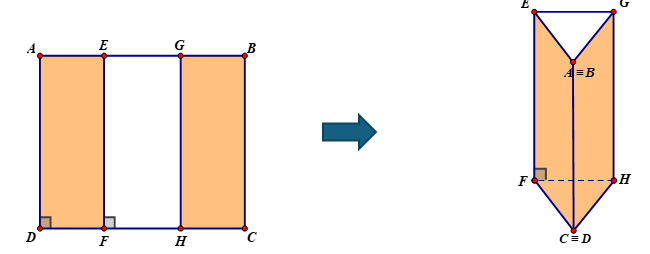
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
Gọi \(p\) là nửa chu vi tam giác \(DHF\).
Ta có: \(DF = CH = x,{\rm{ }}FH = 30 - 2x \Rightarrow p = 15.\)
Thể tích khối lăng trụ như hình vẽ là
\(V = {S_{\Delta FDH}}.EF = 30\sqrt {15(15 - x)(15 - x)(15 - 30 + 2x)} \)\( = 30\sqrt {15{{(15 - x)}^2}(2x - 15)} .\)
Xét hàm số \(f(x) = {(15 - x)^2}(2x - 15)\),\(x \in \left( {\frac{{15}}{2};15} \right)\).
\[f'(x) = - 2(15 - x)(2x - 15) + 2{(15 - x)^2} = - 2(15 - x)(3x - 30)\]; \(f'(x) = 0 \Leftrightarrow \left[ \begin{array}{l}x = 10\left( {TM} \right)\\x = 15\left( {KTM} \right)\end{array} \right.\).
Bảng biến thiên:
Dựa vào bảng biến thiên, ta thấy: \(\mathop {\max }\limits_{\left( {\frac{{15}}{2};15} \right)} f(x) = 125\) khi \(x = 10.\)
Do đó thể tích khối lăng trụ như hình vẽ lớn nhất: \({V_{\max }} = 750\sqrt 3 {\rm{ (c}}{{\rm{m}}^3}).\) Khi đó: \(x = 10{\rm{ (cm)}}{\rm{.}}\)
