Trắc nghiệm Toán 12 Kết nối tri thức Bài 13. Ứng dụng hình học của tích phân có đáp án
Trắc nghiệm Toán 12 Kết nối tri thức Bài 13. Ứng dụng hình học của tích phân có đáp án
-
57 lượt thi
-
20 câu hỏi
-
60 phút
Danh sách câu hỏi
Câu 1:
I. Nhận biết
Thể tích \[V\] của khối tròn xoay giới hạn bởi đồ thị hàm số \[y = f\left( x \right)\], trục \[Ox\] và hai đường thẳng \[x = a,x = b{\rm{ }}\left( {a < b} \right)\] khi quay quanh trục \[Ox\] là:
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
Câu 2:
Diện tích \[S\] của hình phẳng giới hạn bởi đồ thị hàm số \[y = f\left( x \right)\], trục \[Ox\] và hai đường thẳng \[x = a,x = b{\rm{ }}\left( {a < b} \right)\] được tính theo công thức
</>
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Câu 3:
Gọi \[S\] là diện tích hình phẳng giới hạn bởi các đường \[y = f\left( x \right)\], trục hoành và hai đường thẳng \[x = - 3,x = 2\]. Đặt \[a = \int\limits_{ - 3}^1 {f\left( x \right)dx} ,{\rm{ }}b = \int\limits_1^2 {f\left( x \right)dx.} \]
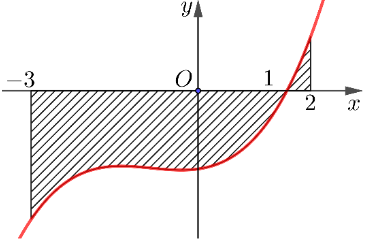
Mệnh đề nào dưới đây là đúng?
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
Ta có: \[S = \int\limits_{ - 3}^2 {\left| {f\left( x \right)} \right|dx = } \int\limits_{ - 3}^1 {\left| {f\left( x \right)} \right|dx} + \int\limits_1^2 {\left| {f\left( x \right)} \right|dx} \]
\[ = - \int\limits_{ - 3}^1 {f\left( x \right)dx} + \int\limits_1^2 {f\left( x \right)dx} \]\[ = b - a.\]
Câu 4:
Gọi \[S\] là diện tích hình phẳng giới hạn bởi các đường \[y = {3^x}\], \[y = 0,x = 0,x = 2.\]Mệnh đề nào dưới đây là đúng?
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
Ta có: \[S = \int\limits_0^2 {\left| {{3^x} - 0} \right|dx} = \int\limits_0^2 {{3^x}dx} .\]
Câu 5:
Cho hàm số \[y = f\left( x \right)\] liên tục trên \[\mathbb{R}.\] Gọi \[S\] là diện tích hình phẳng giới hạn bởi các đường \[y = f\left( x \right)\], \[y = 0,x = - 2,x = 3\] (như hình vẽ). Mệnh đề nào dưới đây là đúng?
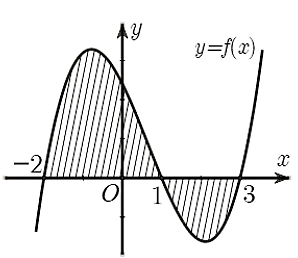
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
Ta có: \[S = \int\limits_{ - 2}^3 {\left| {f\left( x \right)} \right|dx = } \int\limits_{ - 2}^1 {\left| {f\left( x \right)} \right|dx} + \int\limits_1^3 {\left| {f\left( x \right)} \right|dx} \]
\[ = \int\limits_{ - 2}^1 {f\left( x \right)dx} - \int\limits_1^3 {f\left( x \right)dx} .\]
Câu 6:
II. Thông hiểu
Diện tích hình phẳng giới hạn bởi đồ thị hàm số \[y = {\left( {x - 2} \right)^2} - 1\], trục hoành và hai đường thẳng \[x = 1,x = 2\] bằng
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
Ta có: \[S = \int\limits_1^2 {\left| {{{\left( {x - 2} \right)}^2} - 1} \right|dx = } \int\limits_1^2 {\left| {{x^2} - 4x + 3} \right|dx} \]
Có \[{\left( {x - 2} \right)^2} - 1 < 0,\forall x \in \left[ {1;2} \right]\] nên \[S = \int\limits_1^2 {\left( { - {x^2} + 4x - 3} \right)dx} = \left. {\left( { - \frac{{{x^3}}}{3} + 2{x^2} - 3x} \right)} \right|_1^2 = \frac{2}{3}.\]
Câu 7:
Tính diện tích hình phẳng giới hạn bởi các đường \[y = {x^2} + 1,{\rm{ }}x = - 1,{\rm{ }}x = 2\] và trục hoành.
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
Ta có: \[S = \int\limits_{ - 1}^2 {\left| {{x^2} + 1} \right|dx = } \int\limits_{ - 1}^2 {\left( {{x^2} + 1} \right)dx} = \left. {\left( {\frac{{{x^3}}}{3} + x} \right)} \right|_{ - 1}^2 = 6.\]
Câu 8:
Cho hình phẳng D giới hạn bởi đường cong \[y = {x^2} + 1\], trục hoành và các đường thẳng \[x = 0,x = 3\]. Khối tròn xoay tạo thành khi quay D quanh trục hoành có thể tích V bằng
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
Ta có: \[V = \pi \int\limits_0^3 {{{\left( {{x^2} + 1} \right)}^2}dx} = \pi \int\limits_0^3 {\left( {{x^4} + 2{x^2} + 1} \right)dx} \]
\[ = \pi \left. {\left( {\frac{{{x^5}}}{5} + \frac{2}{3}{x^3} + x} \right)} \right|_0^3 = \frac{{348\pi }}{5}.\]
Câu 9:
Diện tích hình phẳng giới hạn bởi đồ thị các hàm số \[y = {x^3} - 6x,y = {x^2}\] (phần tô đậm trong hình sau) bằng:
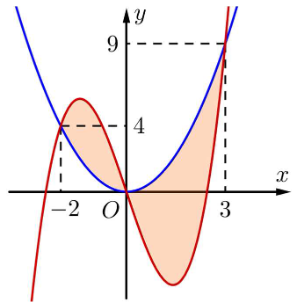
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
Ta có: \[S = \int\limits_{ - 2}^3 {\left| {{x^3} - 6x - {x^2}} \right|} dx = \int\limits_{ - 2}^0 {\left| {{x^3} - 6x - {x^2}} \right|} dx + \int\limits_0^3 {\left| {{x^3} - 6x - {x^2}} \right|} dx\]
\[ = \int\limits_{ - 2}^0 {\left( {{x^3} - 6x - {x^2}} \right)} dx - \int\limits_0^3 {\left( {{x^3} - 6x - {x^2}} \right)} dx\].
Câu 10:
Diện tích hình phẳng giới hạn bởi đồ thị các hàm số \[y = \ln x,{\rm{ }}y = 1\] và hai đường thẳng \[x = 1,x = e\] bằng
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
Ta có: \[S = \int\limits_1^e {\left| {\ln x - 1} \right|dx} = \int\limits_1^e { - \left( {\ln x - 1} \right)dx} \]
\[ = \int\limits_1^e {1dx - \int\limits_1^e {\ln xdx} } \]
Cho \[I = \int {\ln xdx} \], ta đặt: \[\left\{ \begin{array}{l}u = \ln x\\dv = dx\end{array} \right. \Rightarrow \left\{ \begin{array}{l}du = \frac{1}{x}dx\\v = x\end{array} \right.\]
Suy ra \[I = \int {\ln xdx} = x\ln x - \int {x.\frac{1}{x}dx = x\ln x - x} \]
Suy ra \[S = \left. x \right|_1^e - \left. {\left( {x\ln x - x} \right)} \right|_1^e = e - 2.\]
Câu 11:
Cho hình phẳng D giới hạn bởi đường cong \[y = {e^x}\], trục hoành và các đường thẳng \[x = 0,x = 1\]. Thể tích khối tròn xoay tạo thành khi quay D quanh trục hoành có thể tích V bằng
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
Ta có: \[V = \pi \int\limits_0^1 {{e^{2x}}dx} = \left. {\pi \frac{{{e^{2x}}}}{2}} \right|_0^1 = \frac{{\pi \left( {{e^2} - 1} \right)}}{2}\].
Câu 12:
Cho hình phẳng D giới hạn bởi đường cong \[y = \sqrt {2 + \cos x} \], trục hoành và các đường thẳng \[x = 0,x = \frac{\pi }{2}.\] Khối tròn xoay tạo thành khi D quay quanh trục hoành có thể tích V bằng:
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
Ta có: \[V = \pi \int\limits_0^{\frac{\pi }{2}} {{{\left( {\sqrt {2 + \cos x} } \right)}^2}dx = \pi } \int\limits_0^{\frac{\pi }{2}} {\left( {2 + \cos x} \right)dx} \]
\[ = \left. {\pi \left( {2x + \sin x} \right)} \right|_0^{^{\frac{\pi }{2}}} = \pi \left( {\pi + 1} \right).\]
Câu 13:
Cho hình (H) giới hạn bởi các đường \[y = {x^2},x = 1\] và trục hoành. Quay hình (H) quanh trục \[Ox\] ta được khối tròn xoay có thể tích là
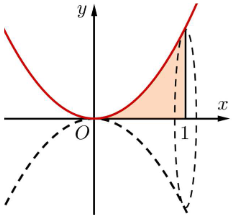
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
Xét phương trình hoành độ giao điểm \[{x^2} = 0 \Rightarrow x = 0\].
Ta có: \[V = \pi \int\limits_0^1 {{{\left( {{x^2}} \right)}^2}} dx = \left. {\pi \frac{{{x^5}}}{5}} \right|_0^1 = \frac{\pi }{5}.\]
Câu 14:
Cho hình phẳng (H) giới hạn bởi các đường \[y = {x^2} - 2x\], trục hoành, trục tung và đường thẳng \[x = 1.\] Tính thể tích V của khối tròn xoay khi quay (H) quanh trục \[Ox.\]
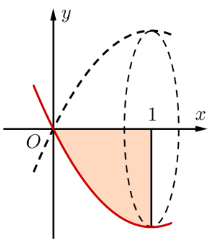
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
Ta có: \[V = \pi \int\limits_0^1 {{{\left( {{x^2} - 2x} \right)}^2}dx = } \pi \int\limits_0^1 {\left( {{x^4} - 4{x^3} + 4{x^2}} \right)dx} \]
\[ = \left. {\pi \left( {\frac{{{x^5}}}{5} - {x^4} + \frac{4}{3}{x^3}} \right)} \right|_0^1 = \frac{{8\pi }}{{15}}.\]
Câu 15:
Tính diện tích hình phẳng giới hạn bởi các đường \[y = {x^2}\], \[y = - \frac{1}{3}x + \frac{4}{3}\] và trục hoành như hình vẽ sau:
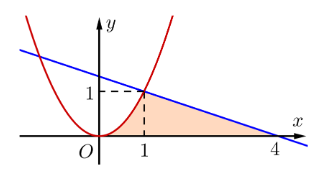
 Xem đáp án
Xem đáp án
Đáp án đúng là:
Diện tích hình phẳng giới hạn bởi đồ thị hàm số \[y = {x^2}\], \[y = - \frac{1}{3}x + \frac{4}{3}\], trục hoành như hình vẽ, ta có: \[S = \int\limits_0^1 {{x^2}dx + \int\limits_1^4 {\left( { - \frac{1}{3}x + \frac{4}{3}} \right)} } dx\]
\[ = \left. {\frac{{{x^3}}}{3}} \right|_0^1 + \left. {\left( { - \frac{1}{6}{x^2} + \frac{4}{3}x} \right)} \right|_1^4 = \frac{{11}}{6}\].
Câu 16:
III. Vận dụng
Một người chạy trong thời gian 1 giờ, vận tốc \[v\] (km/h) phụ thuộc vào thời gian t (h) có đồ thị là một phần parabol với đỉnh \[I\left( {\frac{1}{2};8} \right)\] và trục đối xứng song song với trục tung như hình bên. Tính quãng đường \[s\] người đó chạy được trong khoảng thời gian 45 phút, kể từ khi chạy?
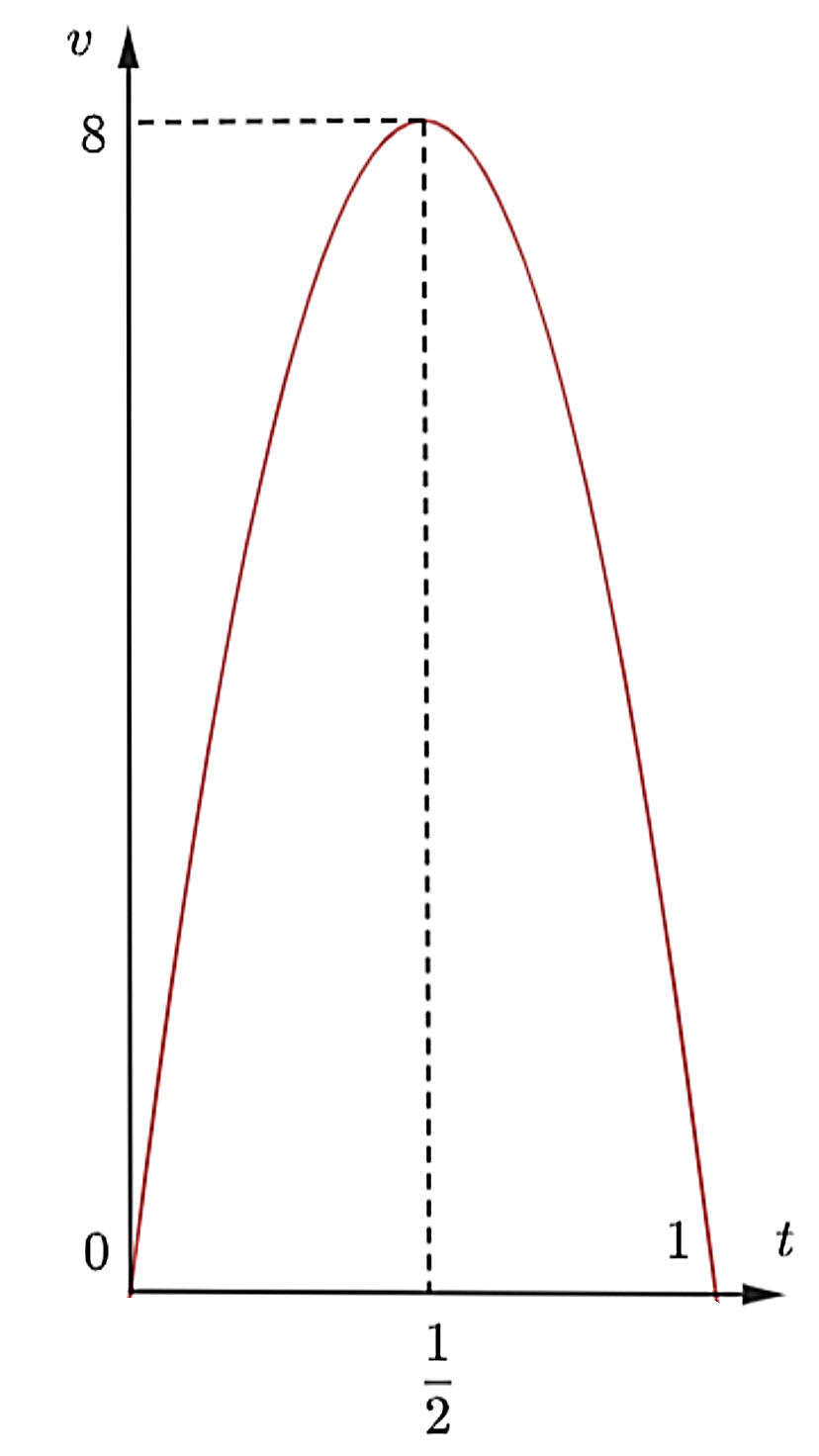
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Gọi parabol là \[\left( P \right):y = a{x^2} + bx + c\]. Từ hình vẽ ta có (P) đi qua điểm có tọa độ (0; 0); (1; 0) và \[I\left( {\frac{1}{2};8} \right)\].
Ta có: \[\left\{ \begin{array}{l}a + b + c = 0\\c = 0\\\frac{a}{4} + \frac{b}{2} + c = 8\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = - 32\\b = 32\\c = 0.\end{array} \right.\]
Suy ra \[\left( P \right):y = - 32{x^2} + 32x.\]
Đổi 45 phút = \[\frac{3}{4}\] giờ.
Vậy quãng đường người đó đi được là
\[s = \int\limits_0^{\frac{3}{4}} {\left( { - 32{x^2} + 32x} \right)dx = \left. {\left( { - \frac{{32}}{3}{x^3} + 16{x^2}} \right)} \right|_0^{\frac{3}{4}} = 4,5} \]km.
Câu 17:
Gọi (H) là hình phẳng giới hạn bởi đồ thị \[\left( C \right):y = \frac{{{x^2} + 1}}{x}\], trục \[Ox\] và hai đường thẳng \[x = 1,x = 3\]. Thể tích V của vật thể tròn xoay khi (H) quay quanh trục \[Ox\] thỏa:
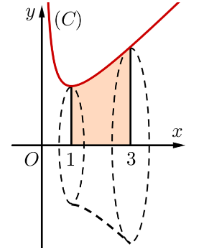
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
Ta có: \[V = \pi \int\limits_1^3 {{{\left( {\frac{{{x^2} + 1}}{x}} \right)}^2}} dx = \pi \int\limits_1^3 {\left( {{x^2} + 2 + \frac{1}{{{x^2}}}} \right)dx} \]
\[ = \left. {\pi \left( {\frac{{{x^3}}}{3} + 2x - \frac{1}{x}} \right)} \right|_1^3 = \frac{{40\pi }}{3} \approx 41,89\].
Vậy \[41 < V < 42.\]
Câu 18:
Cho hình (H) là hình phẳng được tô đậm trong hình vẽ và được giới hạn bởi các đường có phương trình \[y = \frac{{10}}{3}x - {x^2}\], \[y = \left\{ \begin{array}{l} - x,{\rm{ }}x \le 1\\x - 2{\rm{, }}x > 1\end{array} \right.\].
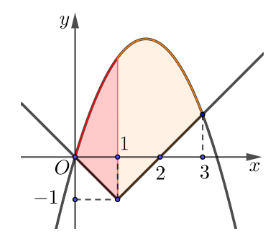
Diện tích của hình (H) bằng
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
Xét \[y = \left\{ \begin{array}{l} - x,{\rm{ }}x \le 1\\x - 2{\rm{, }}x > 1\end{array} \right.\], ta có:
\[\mathop {\lim }\limits_{x \to {1^ + }} y = \mathop {\lim }\limits_{x \to {1^ + }} \left( {x - 2} \right) = - 1\]; \[\mathop {\lim }\limits_{x \to {1^ - }} y = \mathop {\lim }\limits_{x \to {1^ - }} \left( { - x} \right) = - 1\] và \[y\left( 1 \right) = - 1\].
Do đó hàm số liên tục tại \[x = 1.\]
Diện tích hình phẳng cần tính là:
\[S = \int\limits_0^1 {\left( {\frac{{10}}{3}x - {x^2} + x} \right)dx + } \int\limits_1^3 {\left( {\frac{{10}}{3}x - {x^2} - x + 2} \right)dx} \]
\[ = \int\limits_0^1 {\left( {\frac{{13}}{3}x - {x^2}} \right)dx + } \int\limits_1^3 {\left( {\frac{7}{3}x - {x^2} + 2} \right)dx} \]
\[ = \left. {\left( {\frac{{13}}{6}{x^2} - \frac{{{x^3}}}{3}} \right)} \right|_0^1 + \left. {\left( {\frac{7}{6}{x^2} - \frac{{{x^3}}}{3} + 2x} \right)} \right|_1^3 = \frac{{13}}{2} = 6,5.\]
Câu 19:
Chị Minh muốn làm một cái cổng hình parabol như hình vẽ dưới đây. Chiều cao \[GH = 4\] m, chiều rộng \[AB = 4\] m, \[AC = BD = 0,9\] m. Chi Minh làm hai cánh cổng khi đóng lại là hình chữ nhật \[CDEF\] tô đậm có giá là \[1200000\] đồng/m2, còn các phần để trắng để trang trí hoa có giá là \[900000\] đồng/m2. Hỏi tổng số tiền để làm hai phần nói trên gần nhất với số tiền nào dưới đây?
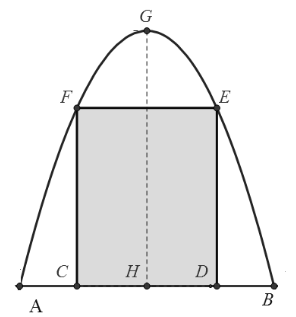
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
Gắn hệ trục tọa độ sao cho \[AB\] trùng \[Ox\], \[A\] trùng \[O\] khi đó parabol có đỉnh \[G\left( {2;4} \right)\] và đi qua gốc tọa độ.
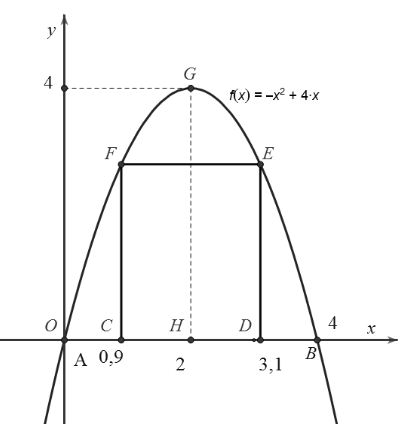
Giả sử phương trình của parabol có dạng \[y = a{x^2} + bx + c{\rm{ }}\left( {a \ne 0} \right).\]
Vì parabol có đỉnh là \[G\left( {2;4} \right)\] và đi qua điểm O(0; 0) nên ta có:
\[\left\{ \begin{array}{l}c = 0\\ - \frac{b}{{2a}} = 2\\4a + 2b + c = 4\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = - 1\\b = 4\\c = 0.\end{array} \right.\]
Suy ra phương trình parabol là \[y = f\left( x \right) = - {x^2} + 4x.\]
Diện tích của cả cổng là \[S = \int\limits_0^4 {\left( { - {x^2} + 4x} \right)dx = \left. {\left( { - \frac{{{x^3}}}{3} + 2{x^2}} \right)} \right|} _0^4 = \frac{{32}}{3}\] (m3).
Mặt khác, ta có chiều cao \[CF = DE = f\left( {0,9} \right) = 2,79\] (m);
\[CD = 4 - 2.0,9 = 2,2\] (m).
Diện tích hai cánh cổng là \[{S_{CDEF}} = CD.CF = 2,79.2,2 = 6,138\] (m2).
Diện tích phần trang trí hoa là: \[{S_{tt}} = S - {S_{CDEF}} = \frac{{32}}{3} - 6,138 = \frac{{6793}}{{1500}}\] (m2).
Vậy tổng số tiền để làm cổng là: \[6,138.1200000 + \frac{{6793}}{{1500}}.900000 = 11441400\] (đồng).
Câu 20:
Một li rượu có hình dạng tròn xoay và kích thước như hình vẽ, thiết diện dọc của cốc (bổ dọc cốc thành 2 phần bằng nhau) là một đường parabol.
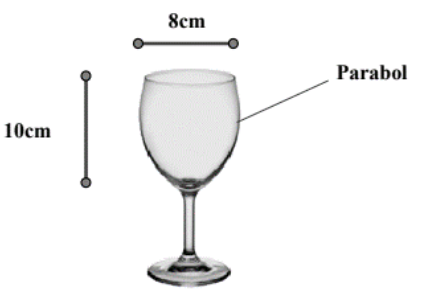
Thể tích tối đa mà cốc có thể chứa được là (làm tròn kết quả đến hai chữ số thập phân).
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Gắn phần miệng li đựng nước vào hệ trục tọa độ, với đỉnh trùng với gốc tọa độ.
Lúc này, ta được parabol đi qua các điểm (0; 0), (−4; 10); (4; 10).
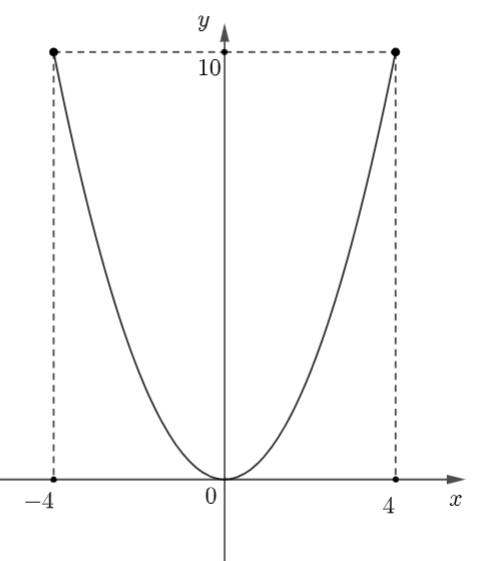
Gọi phương trình parabol là: \[y = a{x^2} + bx + c\] \[\left( {a \ne 0} \right)\].
Ta có: \[\left\{ \begin{array}{l}c = 0\\16a - 4b + c = 10\\16a + 4b + c = 10\end{array} \right. \Rightarrow \left\{ \begin{array}{l}c = 0\\a = \frac{5}{8}\\b = 0\end{array} \right.\].
Vậy \[y = \frac{5}{8}{x^2} \Leftrightarrow {x^2} = \frac{8}{5}y \Leftrightarrow x = \sqrt {\frac{8}{5}y} \]
Thể tích tối đa mà cốc có thể chứa nước là
\[V = \pi {\int\limits_0^{10} {\left( {\sqrt {\frac{8}{5}} y} \right)} ^2}dy = \pi \int\limits_0^{10} {\left( {\frac{8}{5}y} \right)dy = \left. {\pi \frac{4}{5}{y^2}} \right|_0^{10}} = 80\pi \approx 251,33\] cm3.
