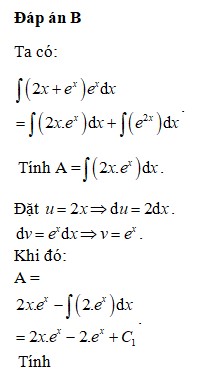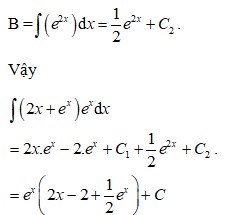15 câu hỏi trắc nghiệm thuộc Trắc nghiệm Nguyên hàm có đáp án (p2) (Thông hiểu)

Câu 1:

Trong các hàm số sau, hàm số nào là một nguyên hàm của $f (x) = \frac{1}{1 - x}$ trên khoảng $(1; + \infty)$

A. $y = \ln |1 - x|$

B. $y = - \ln (1 - x)$

C. $y = \ln \frac{1}{x - 1}$

D. $y = \ln |x - 1|$

Xem đáp án

Câu 2:

Cho hàm số $f (x) = x^{2} + \sin x + 1$ . Biết $F (x)$ là một nguyên hàm của f(x) và F(0)=1 . Tìm F(x) .

A. $F (x) = x^{3} - \cos x + x + 2$

B. $F (x) = \frac{x^{3}}{3} + \cos x + x$

C. $F (x) = \frac{x^{3}}{3} - \cos x + x + 2$

D. $F (x) = \frac{x^{3}}{3} - \cos x + 2$

Xem đáp án

Đáp án C

Câu 3:

Họ nguyên hàm của hàm số $y = e^{x} (1 - \frac{e^{- x}}{\cos^{2} x})$ là

A. $e^{x} + \tan x + C$

B. $e^{x} - \tan x + C$

C. $e^{x} - \frac{1}{\cos x} + C$

D. $e^{x} + \frac{1}{\cos x} + C$

Xem đáp án

Đáp án B

Ta có $\int e^{x} (1 - \frac{e^{- x}}{\cos^{2} x}) d x = \int (e^{x} - \frac{1}{\cos^{2} x}) d x = e^{x} - \tan x + C$

Câu 4:

Họ nguyên hàm của hàm số $f (x) = \frac{2 x + 1}{1 - x}$ trên khoảng $(1; + \infty) .$

A. $- 2 x - 3 \ln (1 - x) + C (C \in ℝ) .$

B. $- 2 x + 3 \ln (x - 1) + C (C \in ℝ) .$

C. $- 2 x + 3 \ln (1 - x) + C (C \in ℝ) .$

D. $- 2 x - 3 \ln (x - 1) + C (C \in ℝ) .$

Xem đáp án

Đáp án D

Ta có: $\int f (x) d x = \int \frac{2 x + 1}{1 - x} d x = \int (- 2 + \frac{3}{1 - x}) d x = - 2 x - 3 \ln |1 - x| + C$

Câu 5:

Họ tất cả các nguyên hàm của hàm số $f (x) = \frac{3 - x}{2 x^{2} + 3 x - 2}$ là

A. $\frac{1}{2} \ln |2 x - 1| - \ln |x + 2| + C$

B. $\ln |2 x - 1| - \ln |x + 2| + C$

C. $\frac{1}{2} \ln (2 x - 1) - \ln (x + 2) + C$

D. $\ln ||2 x - 1| - |x + 2|| + C$

Xem đáp án

Đáp án A

Ta có:

$\int f (x) d x = \int \frac{3 - x}{2 x^{2} + 3 x - 2} d x = \int (\frac{1}{2 x - 1} - \frac{1}{x + 2}) d x = \int \frac{d x}{2 x - 1} - \int \frac{d x}{x + 2} = \frac{1}{2} \ln |2 x - 1| - \ln |x + 2| + C$

Câu 6:

Cho hàm số $f (x) = \frac{1}{x (x + 2)}$ . Mệnh đề nào dưới đây là đúng?

A. $\int f (x) d x = \ln |\frac{x}{x + 2}| + C$

B. $\int f (x) d x = \frac{1}{2} \ln |\frac{x}{x + 2}| + C$

C. $\int f (x) d x = \ln |\frac{x + 2}{x}| + C$

D. $\int f (x) d x = \frac{1}{2} \ln |\frac{x + 2}{x}| + C$

Xem đáp án

Đáp án B

$\begin{array}{l} \int \frac{1}{x (x + 2)} d x = \frac{1}{2} \int \frac{x + 2 - x}{x (x + 2)} d x = \frac{1}{2} \int \frac{1}{x} d x - \frac{1}{2} \int \frac{1}{x + 2} d x \\ = \frac{1}{2} \ln |x| - \frac{1}{2} \ln |x + 2| + C \\ = \frac{1}{2} \ln |\frac{x}{x + 2}| + C \end{array}$

Câu 7:

Họ tất cả các nguyên hàm của hàm số $f (x) = \frac{x + 2019}{x - 1}$ trên khoảng $(1; + \infty)$ là

A. $x + 2020 \ln (x - 1) + C$

B. $x - 2020 \ln (x - 1) + C$

C. $x - \frac{2020}{{(x - 1)}^{2}} + C$

D. $x + \frac{2020}{{(x - 1)}^{2}} + C$

Xem đáp án

Đáp án A

Ta có $\int \frac{x + 2019}{x - 1} d x = \int \frac{x - 1 + 2020}{x - 1} d x = \int (1 + \frac{2020}{x - 1}) d x = x + 2020 \ln |x - 1| + C$

$= x + 2020 \ln (x - 1) + C$

(Vì $x \in (1; + \infty)$ nên $|x - 1| = x - 1$ ).

Câu 8:

Họ nguyên hàm của hàm số $f (x) = x^{2} \sqrt{4 + x^{3}}$ là

A. $\frac{2}{9} \sqrt{{(4 + x^{3})}^{3}} + C$

B. $\frac{1}{9} \sqrt{{(4 + x^{3})}^{3}} + C$

C. $2 \sqrt{x^{3} + 4} + C$

D. $2 \sqrt{{(4 + x^{3})}^{3}} + C$

Xem đáp án

Đáp án A

Ta có $\int f (x) d x = \int x^{2} \sqrt{4 + x^{3}} d x$

Đặt

Câu 9:

Biết $F (x) = e^{x} - 2 x^{2}$ là một nguyên hàm của hàm số f(x) trên R . Khi đó $\int f (2 x) d x$ bằng:

A. $2 e^{x} - 4 x^{2} + C$

B. $\frac{1}{2} e^{2 x} - 4 x^{2} + C$

C. $e^{2 x} - 8 x^{2} + C$

D. $\frac{1}{2} e^{2 x} - 2 x^{2} + C$

Xem đáp án

Đáp án B

$\int f (2 x) d x = \frac{1}{2} \int f (2 x) d (2 x) = \frac{1}{2} F (2 x) = \frac{1}{2} (e^{2 x} - 2 {(2 x)}^{2}) + C$

Câu 10:

Khi tính nguyên hàm $\int \frac{x + 1}{\sqrt{x - 1}} d x$ , bằng cách đặt $u = \sqrt{x - 1}$ ta được nguyên hàm nào?

A. $\int 2 (u^{2} + 2) d u$

B. $\int 2 u (u^{2} + 2) d u$

C. $\int (2 u^{2} + 2) d u$

D. $\int 2 u^{2} d u$

Xem đáp án

Đáp án A

Đặt $u = \sqrt{x - 1}$ $\Rightarrow u^{2} = x - 1 \Rightarrow x = u^{2} + 1 \Rightarrow d x = 2 u d u$ .

Khi đó $\int \frac{x + 1}{\sqrt{x - 1}} d x = \int \frac{u^{2} + 2}{u} .2 u d u = \int 2 (u^{2} + 2) d u$

Câu 11:

Cho F(x) là một nguyên hàm của hàm số $f (x) = \frac{1}{e^{x} + 1}$ thỏa mãn $F (0) = - \ln 2$ . Tìm tập nghiệm S của phương trình $F (x) + \ln (e^{x} + 1) = 3$ .

A. $S = \{\pm 3\}$

B. $S = \{3\}$

C. $S = \emptyset$

D. $S = \{- 3\}$

Xem đáp án

Câu 12:

Biết $\int \ln (x + 3) d x = x \ln (x + 3) + a x + b \ln (x + 3) + C$ . Giá trị của biểu thức $S = 2 a - b$ bằng

A. -7

B. -5

C. -1

D. 5

Xem đáp án

Đáp án B

Đặt $\{\begin{cases} u = \ln (x + 3) \\ d v = d x \end{cases} \Rightarrow \{\begin{cases} d u = \frac{1}{x + 3} d x \\ v = x \end{cases}$

Khi đó:

$\begin{array}{l} \int \ln (x + 3) d x \\ = x \ln (x + 3) - \int \frac{x}{x + 3} d x \end{array}$

$= x \ln (x + 3) - \int (1 - \frac{3}{x + 3}) d x = x \ln (x + 3) - x + 3 \ln (x + 3) + C$

Suy ra: $\{\begin{cases} a = - 1 \\ b = 3 \end{cases}$ . Vậy $S = 2 a - b = - 5$ .

Câu 13:

Hàm số nào sau đây là một nguyên hàm của hàm số $f (x) = x . \cos 2 x$ ?

A. $y = \frac{1}{2} x \sin 2 x + \frac{1}{2} \cos 2 x - 3$

B. $y = \frac{- 1}{2} x \sin 2 x - \frac{1}{4} \cos 2 x + 2$

C. $y = \frac{1}{2} x \sin 2 x + \frac{1}{4} \cos 2 x + 1$

D. $y = \frac{- 1}{2} x \sin 2 x + \frac{1}{4} \cos 2 x - 2$

Xem đáp án

Đáp án C

Đặt $\{\begin{cases} u = x \\ d v = cos2 x d x \end{cases} \Rightarrow \{\begin{cases} d u = d x \\ v = \frac{1}{2} \sin 2 x \end{cases}$

Khi đó $F (x) = \int x . c o s 2 x d x = \frac{1}{2} x \sin 2 x - \int \frac{1}{2} s i n 2 x d x = \frac{1}{2} x \sin 2 x + \frac{1}{4} cos2 x + C$

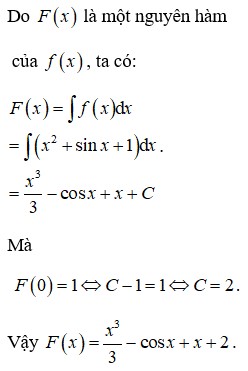
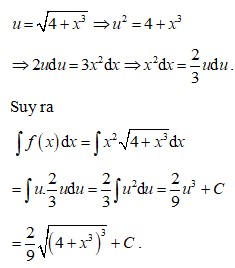
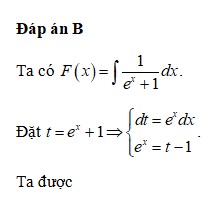
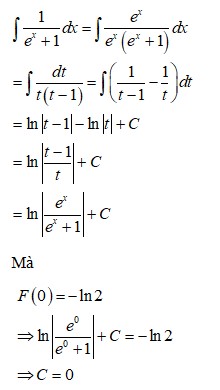
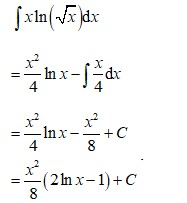Vậy một nguyên hàm của f(x) là $y = \frac{1}{2} x \sin 2 x + \frac{1}{4} \cos 2 x + 1$ .

Câu 14:

Tìm họ nguyên hàm của hàm số $f (x) = x \ln (\sqrt{x})$

A. $\frac{1}{8} x^{2} (2 \ln x - 1) + C$

B. $\frac{1}{4} x^{2} (2 \ln x + 1) + C$

C. $\frac{1}{2} x^{2} (2 \ln x - 1) + C$

D. $\frac{1}{8} x^{2} (2 \ln x + 1) + C$

Xem đáp án

Đáp án A

Đặt $u = \ln (\sqrt{x}) = \frac{1}{2} \ln x \Rightarrow d u = \frac{d x}{2 x}$ , $d v = x d x \Rightarrow v = \frac{x^{2}}{2}$ .

Ta có

.

Câu 15:

Tìm họ nguyên hàm $\int (2 x + e^{x}) e^{x} d x$ .

A. $e^{x} (2 x + 2 + \frac{1}{2} e^{x}) + C$

B. $e^{x} (2 x - 2 + \frac{1}{2} e^{x}) + C$

C. $e^{x} (e^{x} + 2 x - 2) + C$

D. $e^{x} (\frac{1}{2} e^{x} - 2 x + 2) + C$

Xem đáp án