Trắc nghiệm Toán 12 Kết nối tri thức Bài 1. Tính đơn điệu và cực trị của hàm số có đáp án
Trắc nghiệm Toán 12 Kết nối tri thức Bài 1. Tính đơn điệu và cực trị của hàm số có đáp án
-
273 lượt thi
-
20 câu hỏi
-
60 phút
Danh sách câu hỏi
Câu 1:
I. Nhận biết
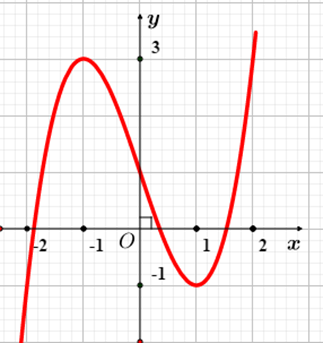
Cho hàm số \(y = f\left( x \right)\) có đồ thị như hình vẽ. Hàm số đã cho đồng biến trên khoảng nào?
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
- Xét đáp án A, trên khoảng \(\left( { - 2\,;2} \right)\) đồ thị có đoạn hướng đi lên là hàm số đồng biến và có đoạn hướng đi xuống là hàm số nghịch biến nên loại.
- Xét đáp án B, trên khoảng \(\left( {0\,;\,2} \right)\) đồ thị có đoạn hướng đi xuống là hàm số nghịch biến và có đoạn hướng đi lên là hàm số đồng biến nên loại.
- Xét đáp án C, trên khoảng \(\left( { - 1\,;\,1} \right)\) đồ thị có hướng đi xuống là hàm số nghịch biến nên loại.
- Xét đáp án D, trên khoảng \(\left( {1\,;\,2} \right)\) đồ thị có hướng đi lên là hàm số đồng biến nên chọn.
Câu 2:
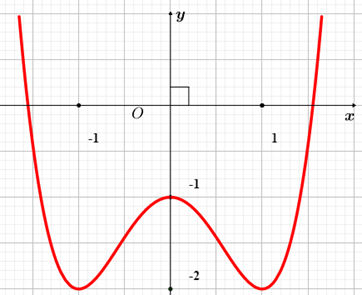
Cho hàm số \(y = f\left( x \right)\) có đồ thị như hình vẽ bên. Hàm số đã cho đồng biến trên khoảng nào dưới đây?
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
Quan sát đồ thị ta thấy đồ thị đi lên trong các khoảng \(( - 1;0)\) và \((1; + \infty ).\)
Vậy hàm số đồng biến trên các khoảng \(( - 1;0)\) và \((1; + \infty ).\)
Câu 3:
Cho hàm số \(y = f\left( x \right)\) có bảng biến thiên như hình vẽ sau
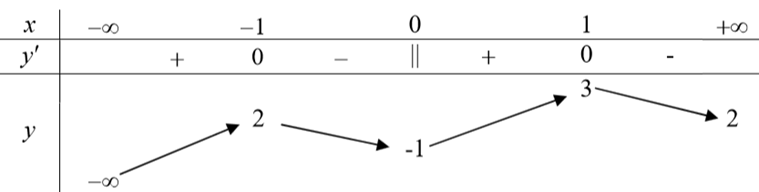
Mệnh đề nào dưới đây đúng?
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
Dựa vào bảng biến thiên ta có hàm số nghịch biến trên khoảng \(\left( {1\,;\,2} \right)\).
Câu 4:
Cho hàm số \(y = f\left( x \right)\) xác định, liên tục trên \(\mathbb{R}\) và có đồ thị là đường cong như hình vẽ.
Hàm số đạt cực đại tại điểm nào dưới đây?
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Từ đồ thị hàm số ta có hàm số đạt cực đại tại \(x = 0\).
Câu 5:
Cho hàm số \(y = f\left( x \right)\) liên tục trên \(\mathbb{R}\) và có bảng biến thiên như sau
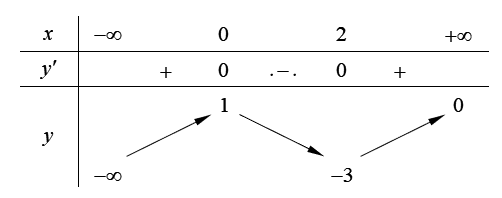
Giá trị cực đại của hàm số \(y = f\left( x \right)\) bằng
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
Dựa vào bảng biến thiên ta có hàm số đạt cực đại tại \[x = 0\]và giá trị cực đại là \[y = 1\].
Câu 6:
II. Thông hiểu
Cho hàm số \[y = {x^3} + 3{x^2} - 9x + 15\]. Khẳng định nào sau đây là khẳng định sai?
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Tập xác định: \[D = \mathbb{R}\].
Ta có \[y' = 3{x^2} + 6x - 9\]; \[y' = 0 \Leftrightarrow \left[ \begin{array}{l}x = 1\\x = - 3\end{array} \right.\].
Bảng biến thiên:
![Cho hàm số \[y = {x^3} + 3{x^2} - 9x + 15\]. Khẳng định nào sau đây là khẳng định sai?D. Hàm số đồng biến trên \[\left( {5; + \infty } \right)\]. (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2024/10/blobid0-1728822942.png)
Kết luận: Hàm số đồng biến trên các khoảng: \[\left( { - \infty ; - 3} \right),\,\,\left( {1; + \infty } \right)\].
Hàm số nghịch biến trên khoảng \[\left( { - 3;1} \right)\].
Câu 7:
Chọn mệnh đề đúng về hàm số \(y = \frac{{2x - 1}}{{x + 2}}\) .
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Tập xác định: \(D = \mathbb{R}\backslash \left\{ { - 2} \right\}\).
Ta có: \(y' = \frac{5}{{{{\left( {x + 2} \right)}^2}}} > 0,\forall x \ne - 2\). Nên hàm số đồng biến trên từng khoảng xác định của nó.
Bảng biến thiên:
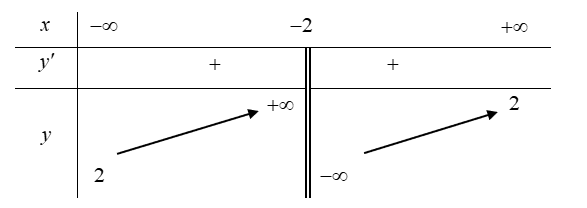
Câu 8:
Hàm số\[y = - {x^3} + 3{x^2} + 1\] nghịch biến khi \[x\] thuộc khoảng nào sau đây?
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
Ta có:\[y' = - 3{x^2} + 6x < 0 \Leftrightarrow x \in \left( { - \infty ;0} \right) \cup \left( {2; + \infty } \right)\].
Câu 9:
Cho hàm số \(y = {x^2}\left( {3 - x} \right)\). Mệnh đề nào sau đây là đúng?
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Ta có \(y = - {x^3} + 3{x^2}\); \[y' = - 3{x^2} + 6x\];
\[y' = 0 \Leftrightarrow \left[ \begin{array}{l}x = 0\\x = 2\end{array} \right.\].
Bảng biến thiên:
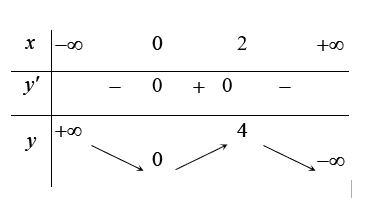
Vậy hàm số đã cho đồng biến trên \[\left( {0;2} \right)\].
Câu 10:
Hàm số nào sau đây nghịch biến trên toàn trục số?
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
Để hàm số nghịch biến trên toàn trục số thì hệ số của \({x^3}\) phải âm. Do đó A & D không thỏa mãn.
Xét B: Ta có \[y' = - 3{x^2} + 6x - 3 = - 3{\left( {x - 1} \right)^2} \le 0,\forall x \in \mathbb{R}\] và \[y' = 0 \Leftrightarrow x = 1\].
Suy ra hàm số này luôn nghịch biến trên \[\mathbb{R}\].
Câu 11:
Hàm số \(y = \frac{{1 - 2x}}{{ - x + 2}}\) có bao nhiêu cực trị?
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
Tập xác định: \(D = \mathbb{R}\backslash \left\{ 2 \right\}\).
Ta có: \(y' = \frac{{ - 3}}{{{{\left( { - x + 2} \right)}^2}}} < 0\), \(\forall x \in D\).
Giới hạn: \(\mathop {\lim }\limits_{x \to \pm \infty } y = 2,\,\,\mathop {\lim }\limits_{x \to {2^ + }} y = + \infty ,\,\,\mathop {\lim }\limits_{x \to {2^ - }} y = - \infty \).
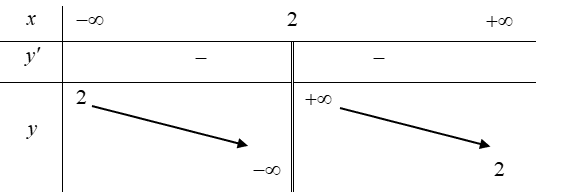
Ta thấy hàm số đã cho không có cực trị.
Câu 12:
Hàm số \(y = \frac{1}{3}{x^3} - 2{x^2} + 4x - 1\) có bao nhiêu điểm cực trị ?
 Xem đáp án
Xem đáp án
Đáp án đúng là: B
\(y' = {x^2} - 4x + 4 = {\left( {x - 2} \right)^2} \ge 0,\forall x \in \mathbb{R}\).
Hàm số không có cực trị.
Câu 13:
Điểm cực tiểu của hàm số \(y = - {x^3} + 3x + 4\) là:
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
TXĐ \(D = \mathbb{R}\).
\(y' = - 3{x^2} + 3 = 0 \Leftrightarrow \left[ \begin{array}{l}x = 1\\x = - 1\end{array} \right.\) .
\(y'\) đổi dấu từ sang khi \(x\) chạy qua \( - 1\) nên hàm số đạt cực tiểu tại \(x = - 1\) .
Câu 14:
Cho hàm số \(y = f\left( x \right)\) liên tục trên \(\mathbb{R}\) và có bảng biến thiên như sau:
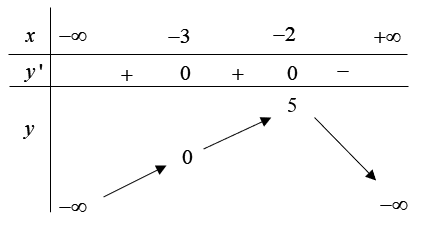
Trong các mệnh đề sau, có bao nhiêu mệnh đề sai?
I. Hàm số đã cho đồng biến trên các khoảng \(\left( { - \infty ; - 5} \right)\) và \(\left( { - 3; - 2} \right)\).
II. Hàm số đã cho đồng biến trên khoảng \(\left( { - \infty ;5} \right)\).
III. Hàm số đã cho nghịch biến trên khoảng \(\left( { - 2; + \infty } \right)\).
IV. Hàm số đã cho đồng biến trên khoảng \(\left( { - \infty ; - 2} \right)\).
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
Nhìn vào bảng biến thiên ta thấy đồ thị hàm số đã cho đồng biến trên khoảng \(\left( { - \infty ; - 2} \right)\); nghịch biến trên khoảng \(\left( { - 2; + \infty } \right)\).
Suy ra II. Sai; III. Đúng; IV. Đúng.
Ta thấy khoảng \(\left( { - \infty ; - 3} \right)\) chứa khoảng \(\left( { - \infty ; - 5} \right)\) nên I Đúng.
Vậy chỉ có II sai.
Câu 15:
Cho hàm số \(y = f\left( x \right)\) có bảng biến thiên như hình dưới đây. Mệnh đề nào sau đây là đúng?
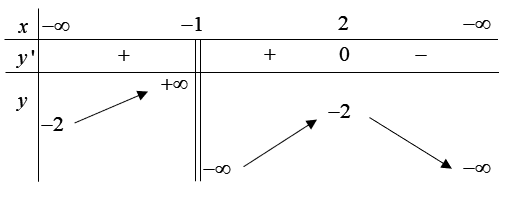
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Vì \(\left( {0;2} \right) \subset \left( { - 1;2} \right)\), mà hàm số đồng biến trên khoảng \(\left( { - 1;2} \right)\) nên suy ra C đúng.
Câu 16:
III. Vận dụng
Cho hàm số \(y = f(x)\). Hàm số \(y = f'(x)\) có đồ thị như hình vẽ:
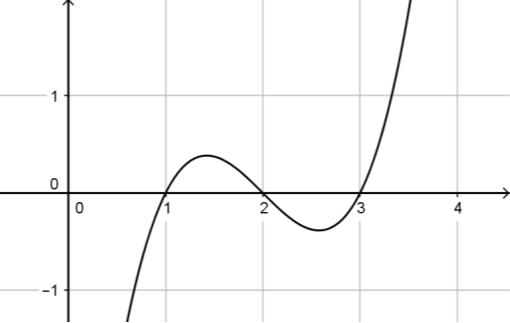
Khẳng định nào sau đây là khẳng định đúng?
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Dựa vào đồ thị hàm số ta có bảng xét dấu sau

Hàm số đạt cực trị tại x = 1; x = 2; x = 3.
Vậy đồ thị hàm số có ba điểm cực trị.
Câu 17:
Cho hàm số \[y = - \frac{1}{3}{x^3} + 4{x^2} - 5x - 17\]. Gọi hoành độ 2 điểm cực trị của đồ thị hàm số là \[{x_1},{x_2}\]. Khi đó, tích số \[{x_1}{x_2}\]có giá trị là:
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
Ta có: \[y' = - {x^2} + 8x - 5\].\[{x_1},{x_2}\]là hai nghiệm của phương trình:\[y' = 0 \Leftrightarrow - {x^2} + 8x - 5 = 0\].Khi đó, theo định lý Viet, ta có: \[{x_1}{x_2} = 5\].
Câu 18:
Cho hàm số \[y = {x^3} - 3{x^2} - 2\]. Gọi \[a,b\]lần lượt là giá trị cực đại và giá trị cực tiểu của hàm số đó. Giá trị của \[2{a^2} + b\] là:
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
\[y' = 3{x^2} - 6x\]
\[y' = 0 \Leftrightarrow \left[ \begin{array}{l}x = 0\\x = 2\end{array} \right.\] .Ta có:\[a = y(0) = - 2;b = y(2) = - 6 \Rightarrow 2a{}^2 + b = 2\].
Câu 19:
Số giá trị \[m\] nguyên để hàm số \(y = \frac{{mx + 2}}{{x + m}}\) nghịch biến trên từng khoảng xác định của nó là
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
Tập xác định \(D = \mathbb{R}\backslash \left\{ { - m} \right\}\).
Hàm số nghịch biến trên từng khoảng xác định của nó \( \Leftrightarrow y' < 0,\forall x \in D.\)
\( \Leftrightarrow \frac{{{m^2} - 2}}{{{{\left( {x + m} \right)}^2}}} < 0,\forall x \in D\)\( \Leftrightarrow {m^2} - 2 < 0 \Leftrightarrow m \in \left( { - \sqrt 2 ;\sqrt 2 } \right) \Rightarrow m \in \left\{ { - 1;0;1} \right\}\).
Câu 20:
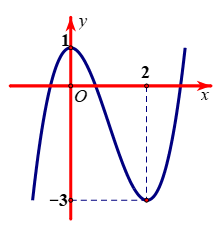
Cho hàm số y = f(x) = x3 + ax2 + bx + c có đồ thị như hình bên dưới.
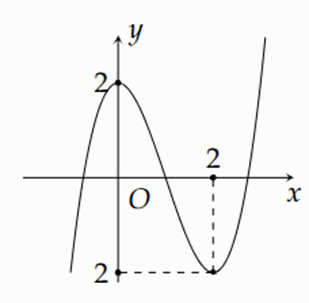
Chọn đáp án sai
 Xem đáp án
Xem đáp án
Hướng dẫn giải
Đáp án đúng là: C
Hàm số y = f(x) có điểm cực tiểu là x = 2, điểm cực đại là x = 0.
Ta có f'(x) = 3x2 + 2ax + b.
Vì 0, 2 là hai nghiệm của phương trình f'(x) = 0 nên b = 0, a = −3.
Vì đồ thị hàm số đi qua điểm có tọa độ (0; 2) nên c = 2. Suy ra f(x) = x3 – 3x2 + 2.
