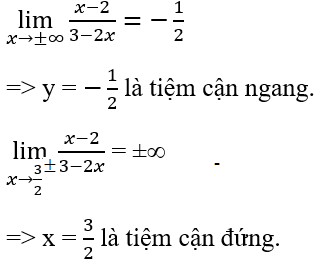30 câu hỏi trắc nghiệm thuộc 250 câu trắc nghiệm Ứng dụng đạo hàm để khảo sát hàm số cơ bản (P7)

Câu 1:

Giá trị nhỏ nhất và giá trị lớn nhất của hàm số $y = - 3 + \sqrt{4 - x^{2}}$ lần lượt là

A. -3 và 0.

B. -3 và -1

C. 0 và 2

D. -2 và 2.

Xem đáp án

Đáp án B.

Điều kiện -2 ≤ x ≤ 2

Câu 2:

Kết luận nào là đúng về giá trị lớn nhất và giá trị nhỏ nhất của hàm số $y = \sqrt{x - x^{2}}$ ?

A. Có giá trị lớn nhất và có giá trị nhỏ nhất

B. Có giá trị nhỏ nhất và không có giá trị lớn nhất

C. Có giá trị lớn nhất và không có giá trị nhỏ nhất

D. Không có giá trị lớn nhất và giá trị nhỏ nhất

Xem đáp án

Đáp án A.

Tập xác định D = [0; 1].

Hàm số đã cho liên tục trên [0; 1] nên luôn có giá trị lớn nhất và giá trị nhỏ nhất trên [0; 1]

Câu 3:

Cho hàm số y = f(x) có $\lim_{x \to + \infty} f (x) = 3$ và $\lim_{x \to - \infty} f (x) = - 3$ Khẳng định nào sau đây là khẳng định đúng?

A. Đồ thị hàm số đã cho có đúng một tiệm cận ngang

B. Đồ thị hàm số đã cho có hai tiệm cận ngang là các đường thẳng x = 3 và x = -3

C. Đồ thị hàm số đã cho có hai tiệm cận ngang là các đường thẳng y = 3 và y = -3

D. Đồ thị hàm số đã cho không có tiệm cận ngang

Xem đáp án

Đáp án C.

Ta có:

=> y = 3, y = -3 là hai tiệm cận ngang.

Câu 4:

Tìm phương trình đường tiệm cận đứng của đồ thị hàm số $y = \frac{x - 1}{x + 2}$

A. x = -2

B. x = 1

C. y = 1

D. x = 2

Xem đáp án

Đáp án A.

Ta có: x = -2 là TCĐ

Câu 5:

Đường tiệm cận ngang của hàm số $y = \frac{x - 3}{2 x + 1}$ là

A. x = 1/2

B. x = -1/2

C. y = -1/2

D. y = 1/2

Xem đáp án

Đáp án D.

Ta có:

Câu 6:

Cho hàm số $y = \frac{2 x - 1}{x + 1}$ . Khẳng định nào sau đây đúng?

A. Đồ thị có tiệm cận đứng x = -1

B. Đồ thị có tiệm cận ngang y = 1

C. Đồ thị có tiệm cận đứng x = 1

D. Đồ thị có tiệm cận ngang y = 3

Xem đáp án

Đáp án A.

Ta có: nên đường thẳng x = -1 là tiệm cận đứng của đồ thị

Câu 7:

Đồ thị hàm số $y = \frac{1 - 2 x}{x - 1}$ có tiệm cận đứng là đường thẳng nào sau đây?

A. x = -2

B. y = -2

C. y = 1

D. x = 1

Xem đáp án

Đáp án D.

Ta có nên đồ thị hàm số có tiệm cận đứng là x = 1

Câu 8:

Tìm tiệm cận đứng của đồ thị hàm số $y = \frac{2 x + 1}{x + 1}$

A. x = 1

B. y = 2

C. x = -1

D. x = -2

Xem đáp án

Đáp án C

Câu 9:

Đường thẳng nào dưới đây là tiệm cận ngang của đồ thị hàm số $y = \frac{2 x + 3}{x + 1}$

A. y = 2

B. y = -1

C. x = 1

D. x = -1

Xem đáp án

Đáp án A.

Vì nên đồ thị hàm số có tiệm cận ngang là y = 2

Câu 10:

Cho hàm số y = f(x) có $\lim_{x \to + \infty} f (x) = 0$ và $\lim_{x \to 0^{+}} f (x) = + \infty$ . Khẳng định nào sau đây là khẳng định đúng?

A. Đồ thị hàm số đã cho không có tiệm cận đứng

B. Trục hoành và trục tung là hai tiệm cận của đồ thị hàm số đã cho

C. Đồ thị hàm số đã cho có một tiệm cận đứng là đường thẳng y = 0

D. Hàm số đã cho có tập xác định là D = (0; +∞)

Xem đáp án

Đáp án B

Câu 11:

Tìm phương trình đường tiệm cận ngang của đồ thị hàm số $y = \frac{1 - x}{x + 1}$

A. y = 1

B. y = -1

C. x = -1

D. x = 1

Xem đáp án

Đáp án A

$\lim_{x \to {(- 1)}^{-}} - \frac{x - 1}{x + 1} = - \infty$

$\lim_{x \to {(- 1)}^{+}} - \frac{x - 1}{x + 1} = + \infty$

Vậy hàm số có đường tiệm cận đứng là x = -1

Câu 12:

Đường thẳng nào sau đây lần lượt là đường tiệm cận đứng, tiệm cận ngang của đồ thị hàm số $y = \frac{2 x + 1}{x + 2}$

A. x = -2, y = 1/2

B. x = 2, y = -2

C. x = 2, y = 2

D. x = -2, y = 2

Xem đáp án

Đáp án D.

Hàm có tiệm cận đứng x = -2 và tiệm cận ngang y = 2

Câu 13:

Tìm tiệm cận đứng của đồ thị hàm số $y = \frac{x - 1}{x + 1}$

A. y = -1

B. x = -1

C. x = 1

D. y = 1

Xem đáp án

Đáp án B.

Tập xác định: D = R \ {-1}

Vậy x = -1 là tiệm cận đứng

Câu 14:

Cho hàm số y = f(x) xác định trên khoảng (0; +∞) và thỏa mãn $\lim_{x \to + \infty} f (x) = 1$ Với giả thiết đó, hãy chọn mệnh đề đúng trong các mệnh đề sau:

A. Đường thẳng y = 1 là tiệm cận ngang của đồ thị hàm số y = f(x)

B. Đường thẳng x = 1 là tiệm cận đứng của đồ thị hàm số y = f(x)

C. Đường thẳng x = 1 là tiệm cận ngang của đồ thị hàm số y = f(x)

D. Đường thẳng y = 1 là tiệm cận đứng của đồ thị hàm số y = f(x)

Xem đáp án

Câu 15:

Cho hàm số y = f(x) xác định trên các khoảng (0; +∞) và thỏa mãn $\lim_{x \to \infty} f (x) = 2$ . Với giả thiết đó, hãy chọn mệnh đề đúng trong các mệnh đề sau?

A. Đường thẳng y = 2 là tiệm cận đứng của đồ thị hàm số y = f(x).

B. Đường thẳng x = 2 là tiệm cận ngang của đồ thị hàm số y = f(x)

C. Đường thẳng y = 2 là tiệm cận ngang của đồ thị hàm số y = f(x)

D. Đường thẳng x = 2 là tiệm cận đứng của đồ thị hàm số y = f(x)

Xem đáp án

Đáp án A

Câu 16:

Tìm tiệm cận đứng của đồ thị hàm số $y = \frac{x - 1}{x + 1}$

A. x = -1

B. x = 1

C. y = -1

D. y = 1

Xem đáp án

Đáp án A

Vậy hàm số có đường tiệm cận đứng là x = -1

Câu 17:

Đồ thị của hàm số nào dưới đây không có đường tiệm cận ?

A.

B.

C. y = x⁴ – 2016

D.

Xem đáp án

Đáp án C.

Vì hàm số y = x⁴ – 2016 là hàm đa thức nên đồ thị hàm số không có đường tiệm cận.

Câu 18:

Cho hàm số Khẳng định nào dưới đây $y = \frac{3 x + 1}{2 x - 1}$ đúng?

A. Đồ thị hàm số không có tiệm cận

B. Đồ thị hàm số có tiệm cận đứng là y = 3/2

C. Đồ thị hàm số có tiệm cận ngang là y = 3/2

D. Đồ thị hàm số có tiệm cận đứng là x = -1/2

Xem đáp án

Đáp án C.

suy ra đồ thị hàm số có tiệm cận ngang là y = 3/2

Câu 19:

Cho hàm số $y = \frac{1}{\sqrt{x - 1}}$ chọn phát biểu đúng trong các phát biểu sau

A. Đồ thị hàm số chỉ có tiệm cận đứng x = 1

B. Đồ thị hàm số chỉ có tiệm cận ngang y = 0

C. Đồ thị hàm số có tiệm cận đứng x = 1 và tiệm cận ngang y = 0

D. Đồ thị hàm số không có tiệm cận đứng

Xem đáp án

Đáp án C.

là đường tiệm cận đứng của đồ thị hàm số.

là đường tiệm cận ngang của đồ thị hàm số.

Câu 20:

Tìm tiệm cận đứng của đồ thị hàm số $y = \frac{x + 1}{x + 2}$

A. x = 1

B. y = 1

C. x = -2

D. y = -2

Xem đáp án

Đáp án C.

Ta có: nên đồ thị hàm số có đường tiệm cận đứng là: x = -2

Câu 21:

Cho hàm số y = f(x) có $\lim_{x \to + \infty} f (x) = 3$ và $\lim_{x \to - \infty} f (x) = - 3$ . Khẳng định nào sau đây là khẳng định đúng:

A. Đồ thị hàm số đã cho không có tiệm cận ngang

B. Đồ thị hàm số đã cho có đúng một tiệm cận ngang

C. Đồ thị hàm số đã cho có hai tiệm cận ngang là các đường thẳng y = 3 và y = -3

D. Đồ thị hàm số đã cho có hai tiệm cận ngang là các đường thẳng x = 3 và x = -3

Xem đáp án

Đáp án C.

=> đồ thị hàm số có hai tiệm cận ngang y = ±3

Câu 22:

Cho hàm số $y = \frac{3 x + 1}{2 x - 1}$ Khẳng định nào sau đây đúng?

A. Đồ thị hàm số có tiệm cận ngang là y = 3/2

B. Đồ thị hàm số có tiệm cận đứng là x = 3/2

C. Đồ thị hàm số có tiệm cận đứng là x = 1

D. Đồ thị hàm số có tiệm cận ngang là y = 2

Xem đáp án

Đáp án A

Câu 23:

Cho hàm số $y = \frac{x - 2}{3 - 2 x}$ có đồ thị (C). Tìm khẳng định đúng.

A. Đồ thị (C) có tiệm cận đứng x = 3/2 và tiệm cận ngang y = -1/2

B. Đồ thị (C) có một đường tiệm cận y = -1/2

C. Đồ thị (C) có tiệm cận đứng x = 3/2 và tiệm cận ngang y = 1/3.

D. Đồ thị (C) có một đường tiệm cận x = 3/2

Xem đáp án

Đáp án A

Câu 24:

Tiệm cận ngang của đồ thị hàm số $y = \frac{x - 1}{3 - 2 x}$ là đường thẳng

A. x = 1/2

B. y = 3/2

C. x = -3/2

D. y = -1/2

Xem đáp án

Đáp án :D.

Câu 25:

Cho đường cong (C): $y = \frac{x - 2}{x + 2}$ . Điểm nào dưới đây là giao của hai tiệm cận của (C)?

A. L(-2;1)

B. M(2;1)

C. N(-2;-2)

D. K(-2;2)

Xem đáp án

Đáp án A.

Đồ thị hàm số có tiệm cận ngang y = 1.

Đồ thị hàm số có tiện cận đứng x = -2

Giao điểm của hai tiệm cận là L(-2;1)

Câu 26:

Đường thẳng nào dưới đây là tiệm cận ngang của đồ thị hàm số $y = \frac{2 x + 1}{3 - x}$

A. y = -2

B. y = 2/3

C. y = 1/3

D. y = 2

Xem đáp án

Câu 27:

Đường thẳng x = 1 là tiệm cận đứng của đồ thị hàm số nào sau đây?

A.

B.

C.

D.

Xem đáp án

Đáp án C

Câu 28:

Tìm đường tiệm cận đứng của đồ thị hàm số $y = \frac{2 x - 1}{x - 1}$

A. x = 1

B. x = 2

C. y = 1

D. y = 2

Xem đáp án

Đáp án A

=> đường x = 1 là tiệm cận đứng.

Câu 29:

Cho hàm số $y = \frac{2 x - 3}{x + 1}$ Hỏi trong các khẳng định sau, khẳng định nào đúng?

A. Hàm số luôn nghịch biến trên miền xác định của nó.

B. Hàm số luôn đồng biến trên tập số thực R

C. Hàm số có tập xác định là D = R \ {1}

D. Đồ thị hàm số có đường tiệm cận ngang là y = 2

Xem đáp án

Đáp án D

Vì

nên đồ thị hàm số có đường tiệm cận ngang là y = 2

Câu 30:

Đường thẳng nào dưới đây là tiệm cận ngang của đồ thị hàm số $y = \frac{3 x - 1}{x - 1}$

A. x = 3

B. y = 3

C. x = 1

D. y = 1

Xem đáp án

Đáp án B.

Ta có:

Do đó y = 3 là tiệm cận ngang của đồ thị hàm số