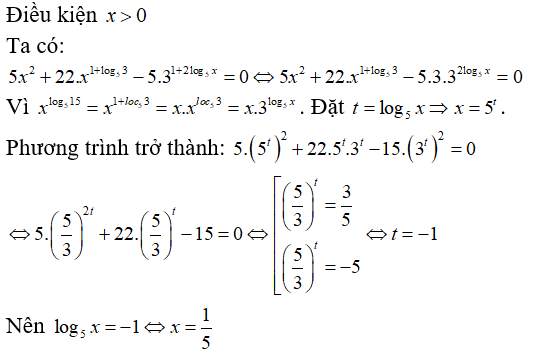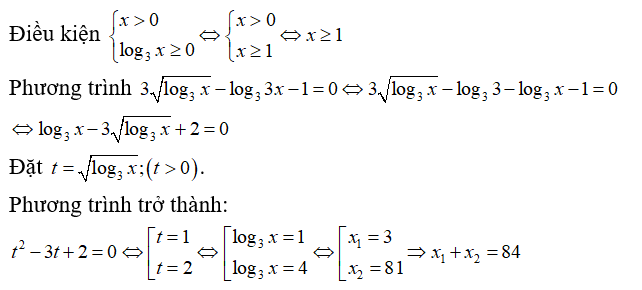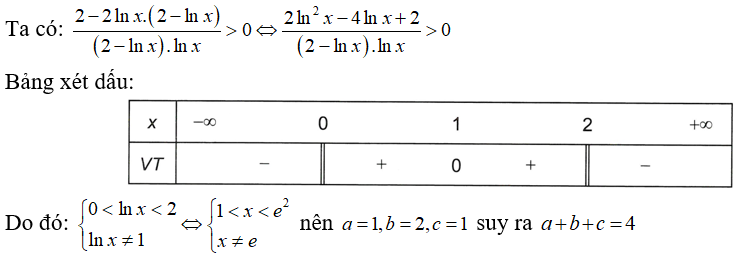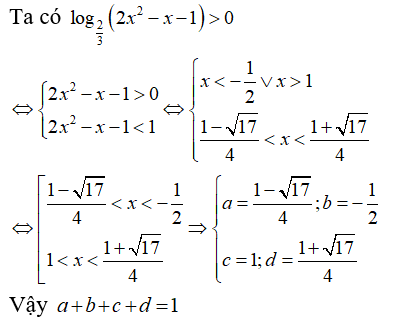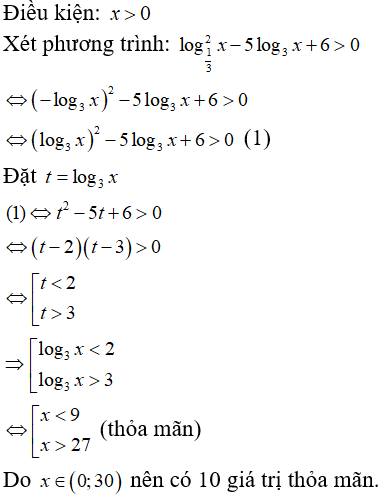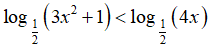188 câu hỏi trắc nghiệm thuộc Chuyên đề Toán 12 Bài 5: Phương trình lôgarit - Bất phương trình lôgarit có đáp án

Câu 1:

\log_{3} (x^{2} - x + 1) = - \log_{\frac{1}{3}} (2 x - 1)

là

A. 0

B. 2

C. 6

D. 3

Xem đáp án

Ta có: $\log_{3} (x^{2} - x + 1) = \log_{3} (2 x - 1) \Leftrightarrow \{\begin{cases} 2 x - 1 > 0 \\ x^{2} - x + 1 = 2 x + 1 \end{cases} \Leftrightarrow \{\begin{cases} x > \frac{1}{2} \\ [\begin{array}{l} x = 0 \\ x = 3 \end{array} \end{cases} \Leftrightarrow x = 3$

Nên phương trình chỉ có một nghiệm là x = 3.

Chọn D.

Câu 2:

Số nghiệm của phương trình $\log_{2} x + \log_{3} x + \log_{4} x = \log_{20} x$ là

A. 1

B. 2

C. 3

D. 4

Xem đáp án

Ta có: $\log_{2} x + \log_{3} 2. \log_{2} x + \log_{4} 2. \log_{2} x = \log_{20} 2. \log_{2} x$

$\Leftrightarrow \log_{2} x . (1 + \log_{3} 2 + \log_{4} 2 - \log_{20} 2) = 0 \Leftrightarrow \log_{2} x = 0 \Leftrightarrow x = 1$

Nên phương trình có duy nhất một nghiệm.

Chọn A.

Câu 3:

Cho phương trình $\log_{4} {(x + 1)}^{2} + 2 = \log_{\sqrt{2}} \sqrt{4 - x} + \log_{8} {(4 + x)}^{3}$ . Tổng tất cả các nghiệm của phương trình là

A.

2 \sqrt{6} - 4

B. 2

C. 4

D.

2 \sqrt{6}

Xem đáp án

Điều kiện: $\{\begin{cases} {(x + 1)}^{2} > 0 \\ 4 - x > 0 \\ {(4 + x)}^{3} > 0 \end{cases} \Leftrightarrow \{\begin{cases} x \neq - 1 \\ x < 4 \\ x > - 4 \end{cases} \Leftrightarrow \{\begin{cases} - 4 < x < 4 \\ x \neq - 1 \end{cases}$

Ta có: $\log_{2} |x + 1| + \log_{2} 4 = \log_{2} (4 - x) + \log_{2} (4 + x) \Leftrightarrow 4 |x - 1| = 16 - x^{2}$

$\Leftrightarrow [\begin{array}{l} \{\begin{cases} x \geq 1 \\ 4 x - 4 = 16 - x^{2} \end{cases} \\ \{\begin{cases} x < 1 \\ - 4 x + 4 = 16 - x^{2} \end{cases} \end{array} \Leftrightarrow [\begin{array}{l} x = - 2 + 2 \sqrt{6} \\ x = - 2 \end{array}$ (thỏa mãn điều kiện).

Tổng tất cả các nghiệm của phương trình là $x = 2 \sqrt{6} - 4$ .

Chọn A.

Câu 4:

Cho phương trình $\log_{2} (\log_{3} (\log_{2} x)) = 1$ . Gọi a là nghiệm của phương trình, biểu thức nào sau đây là đúng?

A. $\log_{2} a = 10$

B.

\log_{2} a = 8

C.

\log_{2} a = 7

D.

\log_{2} a = 9

Xem đáp án

Điều kiện $x > 0; \log_{2} x > 0; \log_{3} (\log_{2} x) > 0$ suy ra $x > 2$

Khi đó $\log_{2} (\log_{3} (\log_{2} x)) = 1 \Leftrightarrow x = 2^{9} \Rightarrow a = 2^{9} \Rightarrow \log_{2} a = 9$

Chọn D.

Câu 5:

Tìm nghiệm của phương trình $\log |x| = |\log x|$ .

A. $S = (1; + \infty)$

B.

S = (0; + \infty)

C.

S = \{1; 10\}

D.

S = [1; + \infty)

Xem đáp án

Điều kiện $\{\begin{matrix} |x| > 0 \\ x > 0 \end{matrix} \Leftrightarrow x > 0$ (*).

Kết hợp với (*) ta được $x \in [1; + \infty)$ thỏa mãn.

Vậy $S = [1; + \infty)$

Chọn D.

Câu 6:

Phương trình ${\log^{2}}_{\sqrt{2}} x + 3 \log_{2} x + \log_{\frac{1}{2}} x = 2$ có hai nghiệm $x_{1}, x_{2}$ . Khi đó $|x_{1} - x_{2}|$ bằng

A. $\sqrt{2} - \frac{1}{2}$

B.

\sqrt{5}

C.

2^{\frac{- 1 + \sqrt{5}}{2}} - 2^{\frac{- 1 - \sqrt{5}}{2}}

D.

\frac{1}{2} - \sqrt{2}

Xem đáp án

Ta có:

$4 {\log^{2}}_{2} x + 3 \log_{2} x - \log_{2} x - 2 = 0$

$\Leftrightarrow 4 {\log^{2}}_{2} x + 2 \log_{2} x - 2 = 0$

$\Leftrightarrow [\begin{array}{l} \log_{2} x = - 1 \\ \log_{2} x = \frac{1}{2} \end{array} \Leftrightarrow [\begin{array}{l} x = \frac{1}{2} \\ x = \sqrt{2} \end{array}$

Khi đó $|x_{1} - x_{2}| = \sqrt{2} - \frac{1}{2}$

Chọn A.

Câu 7:

Phương trình $\log_{3} (3^{x} - 1) . \log_{3} (3^{x + 1} - 3) = 6$ có

A. hai nghiệm dương

B. một nghiệm dương

D. một nghiệm kép

Xem đáp án

Ta có: $\log_{3} (3^{x} - 1) . \log_{3} (3^{x + 1} - 3) = 6 \Leftrightarrow \log_{3} (3^{x} - 1) . \log_{3} ({3.3}^{x} - 3) = 6$

\Leftrightarrow \log_{3} (3^{x} - 1) . \log_{3} [3. (3^{x} - 1)] = 6 \Leftrightarrow \log_{3} (3^{x} - 1) . [1 + \log_{3} (3^{x} - 1)] = 6

\Leftrightarrow {[\log_{3} (3^{x} - 1)]}^{2} + \log_{3} (3^{x} - 1) - 6 = 0 \Leftrightarrow [\begin{array}{l} \log_{3} (3^{x} - 1) = 2 \\ \log_{3} (3^{x} - 1) = - 3 \end{array}

\Leftrightarrow [\begin{array}{l} 3^{x} - 1 = 9 \\ 3^{x} - 1 = \frac{1}{27} \end{array} \Leftrightarrow [\begin{array}{l} 3^{x} = 10 \\ 3^{x} = \frac{28}{27} \end{array} \Leftrightarrow [\begin{array}{l} x = \log_{3} 10 \\ x = \log_{3} \frac{28}{27} \end{array}

Chọn A.

Câu 8:

Phương trình $\log_{3} (x + 2) + \log_{7} (3 x + 4) = 2$ có bao nhiêu nghiệm?

A. 1

B. 0

C. 2

D. 3

Xem đáp án

Phương trình log 3( x + 2) + log 7( 3x +4) = 2 có bao nhiêu nghiệm? (ảnh 1)

Chọn A.

Câu 9:

Phương trình $\ln (x^{2} + x + 1) - \ln (2 x^{2} + 1) = x^{2} - x$ có tổng bình phương các nghiệm bằng

A. 5

B. 25

C. 9

D. 1

Xem đáp án

Phương trình ln( x^2 + x + 1) -ln( 2x^2 +1) = x^2 - x có tổng bình phương các nghiệm bằng (ảnh 1)

Chọn D.

Câu 10:

Số nghiệm của phương trình $\ln (x - 1) = \frac{1}{x - 2}$ là

A. 1

B. 0

C. 3

D. 2

Xem đáp án

Số nghiệm của phương trình ln(x - 1) = 1/x -2 là (ảnh 1)

Chọn A.

Câu 11:

Số nghiệm của phương trình $\log_{3} |x^{2} - \sqrt{2} x| = \log_{5} (x^{2} - \sqrt{2} x + 2)$ là

A. 3

B. 2

C. 1

D. 4

Xem đáp án

Số nghiệm của phương trình log 3 trị x^2 - căn 2 x = log 5( x^2 - căn 2 x + 2) là (ảnh 1)

Chọn B.

Câu 12:

Biết rằng phương trình $\log_{2} (1 + x^{1009}) = 2018 \log_{3} x$ có nghiệm duy nhất $x_{0}$ . Khẳng định nào dưới đây đúng?

A. $3^{\frac{1}{1008}} < x_{0} < 3^{\frac{1}{1006}}$

B.

x_{0} > 3^{\frac{2}{1009}}

C.

1 < x_{0} < 3^{\frac{1}{1008}}

D.

3^{\frac{1}{1007}} < x_{0} < 1

Xem đáp án

Biết rằng phương trình log 2 ( 1+ x^ 1009) = 2018 log 3 x có nghiệm duy nhất xo . Khẳng định nào dưới đây đúng? (ảnh 1)

Chọn C.

Câu 13:

Xét các số nguyên dương a,b sao cho phương trình $a \ln^{2} x + b \ln x + 5 = 0$ có hai nghiệm phân biệt $x_{1}, x_{2}$ và phương trình $5 \log^{2} x + b \log x + a = 0$ có hai nghiệm phân biệt $x_{3}, x_{4}$ thỏa mãn $x_{1} x_{2} > x_{3} x_{4}$ . Tính giá trị nhỏ nhất $S_{\min}$ của S = 2a + 3b.

A. $S_{\min} = 30$

B.

S_{\min} = 25

C.

S_{\min} = 33

D.

S_{\min} = 17

Xem đáp án

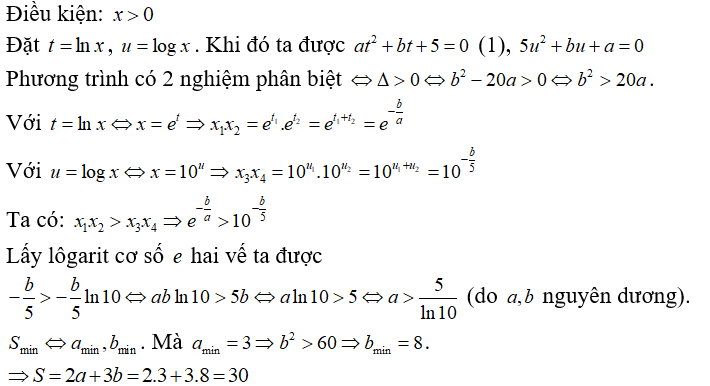
Xét các số nguyên dương a,b sao cho phương trình aln^2 x + bln x + 5 = 0 có hai nghiệm phân biệt (ảnh 1)

Chọn A.

Câu 14:

Phương trình $8^{\log_{2} (x^{2} - 8)} = {(x - 2)}^{3}$ có tất cả bao nhiêu nghiệm phân biệt?

A. 0

B. 2

C. 1

D. 3

Xem đáp án

Phương trình 8^ log 2( x^2 - 8) =( (x - 2)^ 3 có tất cả bao nhiêu nghiệm phân biệt? (ảnh 1)

Chọn C.

Câu 15:

Phương trình

5 x^{2} + 22. x^{\log_{5} 15} - {5.3}^{\log_{5} 5 x^{2}} = 0

có tất cả bao nhiêu nghiệm?

A. 0

B. 2

C. 1

D. 3

Xem đáp án

Phương trình 5x^2 + 22x ^log 5 15 - 5. 3^ ^ log 5x^2 có tất cả bao nhiêu nghiệm? (ảnh 1)

Chọn C.

Câu 16:

Biết phương trình $\log_{2} x - \log_{x} 64 = 1$ có hai nghiệm phân biệt. Khi đó tích hai nghiệm này bằng

A. 2

B. 1

C.

\frac{1}{4}

D.

\frac{1}{2}

Xem đáp án

Biết phương trình log 2x - log x 64 =1 có hai nghiệm phân biệt. Khi đó tích hai nghiệm này bằng (ảnh 1)

Chọn A.

Câu 17:

Tổng tất cả các nghiệm của phương trình $3 \sqrt{\log_{3} x} - \log_{3} 3 x - 1 = 0$ bằng

A. 35

B. 84

C. 65

D. 28

Xem đáp án

Tổng tất cả các nghiệm của phương trình 3 căn log 3 x - log 3 3x - 1 = 0 bằng (ảnh 1)

Chọn B.

Câu 18:

Phương trình $\log_{3}^{2} x + (x - 12) \log_{3} x + 11 - x = 0$ có tất cả bao nhiêu nghiệm?

A. 0

B. 2

C. 1

D. 3

Xem đáp án

Phương trình log 3 x^2 + ( x - 12)log 3 x + 11 - x = 0 có tất cả bao nhiêu nghiệm? (ảnh 1)

Chọn B.

Câu 19:

Tổng các nghiệm của phương trình $2 \log^{2} x - \ln x = 2 \ln x . \log x - \log x$ là một số có dạng $\frac{a + \sqrt{b}}{\sqrt{b}}$ với a,b là các số nguyên dương. Giá trị của a + b là

A. 11

B. 13

C. 3

D. 5

Xem đáp án

Tổng các nghiệm của phương trình 2log^2x -ln = 2lnx. log x - log x là một số có dạng (ảnh 1)

Chọn A.

Câu 20:

Có bao nhiêu giá trị nguyên của tham số $m \in (- 10; 10)$ để phương trình $\log_{3}^{2} x + \log_{3} x + m = 0$ có nghiệm?

A. 11

B. 10

C. 12

D. 5

Xem đáp án

Tập xác định $D = (0; + \infty)$ . Đặt $\log_{3} x = t$ .

Khi đó phương trình trở thành $t^{2} + t + m = 0$ (*)

Phương trình đã cho có nghiệm khi phương trình (*) có nghiệm: $Δ = 1 - 4 m \geq 0 \Leftrightarrow m \leq \frac{1}{4}$

Vậy để phương trình có nghiệm thực thì $m \leq \frac{1}{4}$

Chọn B.

Câu 21:

Có bao nhiêu giá trị nguyên của tham số $m \in (- 10; 10)$ để phương trình $\log_{2} (5^{x} - 1) \log_{4} ({2.5}^{x} - 2) = m$ có nghiệm $x \geq 1$ ?

A. 6

B. 8

C. 9

D. 7

Xem đáp án

Có bao nhiêu giá trị nguyên của tham số m thuộc -10;10 để phương trình log 2( 5^x - 1) log 4( 2.5^x -2)= m có nghiệm ? (ảnh 1)

Chọn D.

Câu 22:

Có bao nhiêu giá trị nguyên của tham số $m \in (- 10; 10)$ để phương trình $\frac{\log (m x)}{\log (x + 1)} = 2$ có nghiệm thực duy nhất?

A. 11

B. 16

C. 12

D. 15

Xem đáp án

Có bao nhiêu giá trị nguyên của tham số m thuộc -10;10 để phương trình log mx/ log (x +1) = 2 có nghiệm thực duy nhất? (ảnh 1)

Chọn D.

Câu 23:

Có bao nhiêu giá trị nguyên của tham số $m \in (- 10; 10)$ để phương trình $m \log_{\frac{1}{2}}^{2} (x - 4) - 2 (m^{2} + 1) \log_{\frac{1}{2}} (x - 4) + m^{3} + m + 2 = 0$ có hai nghiệm thực phân biệt trong khoảng $(4; 6)$ ?

A. 6

B. 8

C. 9

D. 7

Xem đáp án

Có bao nhiêu giá trị nguyên của tham số m thuộc -10;10 để phương trình mlog 1/2( x - 4)^2 -2( m^2 + 1) log 1/2 ( x -4) + m^3 + m + 2 =0 (ảnh 1)

Chọn B.

Câu 24:

Có bao nhiêu giá trị nguyên của tham số m để $\log_{3}^{2} x + \sqrt{\log_{3}^{2} x + 1} - 2 m - 1 = 0$ có nghiệm trong đoạn $[1; 3^{\sqrt{3}}]$ ?

A. 6

B. 4

C. 1

D. 0

Xem đáp án

Có bao nhiêu giá trị nguyên của tham số m để log 3x^2 + căn log 3x^2 + 1 - 2m - 1 =0 có nghiệm trong đoạn (ảnh 1)

Chọn C.

Câu 25:

Tìm các giá trị của tham số m để phương trình $\log_{3}^{2} x + \sqrt{\log_{3}^{2} x + 1} - 2 m - 1 = 0$ có nghiệm thuộc khoảng $(0; 1)$ .

A.

m \in (0; \frac{1}{4}]

B.

m \in (- \infty; \frac{1}{4}]

C.

m \in (- \infty; 0]

D.

m \in [\frac{1}{4}; + \infty)

Xem đáp án

Tìm các giá trị của tham số m để phương trình log 3x^2 + căn log 3x^2 + 1 - 2m - 1 = 0 có nghiệm thuộc khoảng (0;1) . (ảnh 1)

Chọn B.

Câu 26:

Có bao nhiêu giá trị nguyên của tham số $m \in (- 10; 10)$ để phương trình $(m - 4) \log_{2}^{2} x - 2 (m - 2) \log_{2} x + m - 1 = 0$ có hai nghiệm thỏa mãn $1 < x_{1} < 2 < x_{2}$ ?

A. 5

B. 4

C. 1

D. 0

Xem đáp án

Có bao nhiêu giá trị nguyên của tham số m thuộc -10;10 để phương trình (m-4)log2x^2 -2( (m -2) log 2x + m - 1 = 0 có hai nghiệm thỏa mãn (ảnh 1)

Chọn A.

Câu 27:

Nghiệm phương trìnhlà $\log_{4} (x - 1) = 3$

A. x = 63

B. x = 82

C. x = 80

D. x = 65

Xem đáp án

Đáp án D

Câu 28:

Tổng các nghiệm không âm của phương trình $\log_{\sqrt{3}} x - \log_{3} (2 x^{2} - 4 x + 3) = 0$ là

A. 1

B. 2

C. 3

D. 4

Xem đáp án

Đáp án D

Câu 29:

Phương trình $\log_{2} (4 - 2^{x}) = 2 - x$ tương đương với phương trình nào sau đây?

A. $4 - 2^{x} = 2 - x$

B.

4 - 2^{x} = 2^{2 - x}

C.

{(2^{x})}^{2} - {4.2}^{x} + 4 = 0

D. Cả 3 đáp án đều sai

Xem đáp án

Đáp án B

Câu 30:

Cho phương trình $\log_{a} (x^{2} + 3 x) = \log_{\sqrt{a}} 2 x, (a > 0; a \neq 1)$ , số nghiệm của phương trình trên là

A. 1

B. 2

C. 3

D. 4

Xem đáp án

Đáp án A

Câu 31:

Phương trình $\log_{a^{3} + 2} 3 - \log_{4 - a} 3 = 0$ có bao nhiêu nghiệm?

A. 0

B. 1

C. 2

D. 3

Xem đáp án

Đáp án B

Câu 32:

Một học sinh giải phương trình $\log_{2}^{2} x - \log_{2} x^{2} + 1 = 0$ theo các bước như sau:

Bước 1: Điều kiện $\{\begin{cases} x > 0 \\ x^{2} > 0 \end{cases} \Leftrightarrow \{\begin{cases} x > 0 \\ x \neq 0 \end{cases} \Leftrightarrow x > 0$

Bước 2: Từ điều kiện trên phương trình đã cho trở thành:

${(\log_{2} x)}^{2} - 2 \log_{2} x + 1 = 0 \Leftrightarrow \log_{2} x = 1$

Bước 3: Vậy nghiệm phương trình là $x = 2^{1} = 2$ (nhận)

Lời giải trên sai ở bước nào?

A. Bước 1

B. Bước 2

C. Bước 3

D. Không sai bước nào

Xem đáp án

Đáp án D

Câu 33:

Nghiệm của phương trình

\log_{0,4} (x - 3) + 2 = 0

là

A. Vô nghiệm

B. Có nghiệm

\forall x > 3

C. x = 2

D.

x = \frac{37}{4}

Xem đáp án

Đáp án D

Câu 34:

Phương trình ${(\ln x)}^{2} - 7 \ln x + 6 = 0$ có bao nhiêu nghiệm?

A. 1

B. 2

C. 3

D. 4

Xem đáp án

Đáp án C

Câu 35:

Nghiệm của phương trình $\log_{\frac{π}{3}} (\log_{2} (x - 3)) = 0$ là?

A. 3

B. 2

C. 4

D. 5

Xem đáp án

Đáp án D

Câu 36:

Với giá trị m bằng bao nhiêu thì phương trình $\log_{2 + \sqrt{3}} (m x + 3) + \log_{2 - \sqrt{3}} (m^{2} + 1)$ có nghiệm là -1?

A.

[\begin{array}{l} m = 1 \\ m = - 1 \end{array}

B.

[\begin{array}{l} m = 1 \\ m = - 2 \end{array}

C.

m < 3

D.

m > 3

Xem đáp án

Đáp án B

Câu 37:

Phương trình $\log_{2} (2 x - 1) - \log_{\frac{1}{2}} (x - 1) = 1$ có nghiệm là

A.

[\begin{array}{l} x = \frac{3 + \sqrt{17}}{4} \\ x = \frac{3 - \sqrt{17}}{4} \end{array}

B.

x = \frac{3 + \sqrt{17}}{4}

C.

x = \frac{3 - \sqrt{17}}{4}

D. x = 1

Xem đáp án

Đáp án B

Câu 38:

Tập nghiệm của phương trình $\log_{\sqrt{3}} |x - 1| = 2$ là

A.

\{3\}

B.

\{- 3; 4\}

C.

\{- 2; - 3\}

D.

\{4; - 2\}

Xem đáp án

Đáp án D

Câu 39:

Tất cả các giá trị x thỏa mãn $x + 2 = 3^{\log_{3} (x + 2)}$ là

A.

x \neq - 2

B.

x \in ℝ

C.

x \geq - 2

D.

x > - 2

Xem đáp án

Đáp án D

Câu 40:

Với giá trị nào của m thì phương trình $\log_{2} (4^{x} + 2 m^{3}) = x$ có hai nghiệm phân biệt?

A.

m < \frac{1}{2}

B.

m > - \sqrt[3]{\frac{4^{x}}{2}}

C.

0 < m < \frac{1}{2}

D.

m > 0

Xem đáp án

Đáp án C

Câu 41:

Phương trình $\log_{3} (3^{x} - 1) . \log_{3} (3^{x + 1} - 3) = 6$ có

A. hai nghiệm dương

B. một nghiệm dương

C. phương trình vô nghiệm

D. một nghiệm kép

Xem đáp án

Đáp án A

Câu 42:

Phương trình $\log_{\sqrt{a}} \sqrt{2 a - x} + \log_{\frac{1}{a}} x = 0$ có nghiệm là

A. x = a

B. x = 2a

C. x = 2a + 1

D. Phương trình vô nghiệm

Xem đáp án

Đáp án A

Câu 43:

Cho phương trình $\log_{3} (\log_{2} \sqrt{x^{2} + 5}) = 1$ , tổng bình phương các nghiệm của phương trình trên là

A. 0

B. 244

C. 59

D. 118

Xem đáp án

Đáp án D

Câu 44:

Phương trình

\log_{3} (\sqrt{x} + 2) = \log_{7} x

có nghiệm là

A. x = 4

B. x = 49

C. x =25

D. Đáp án khác

Xem đáp án

Đáp án B

Câu 45:

Với giá trị nào của m thì phương trình $\log_{3}^{2} x + \sqrt{\log_{3}^{2} x + 1} = 3 m$ có nghiệm trên [1;3]?

A. $m \in (1 + \sqrt{2}; 1)$

B.

m \in [\frac{1}{3}; \frac{1 + \sqrt{2}}{3}]

C.

m \in (- \infty; \frac{1}{3}]

D.

m \in (\frac{1 + \sqrt{2}}{3}; 1]

Xem đáp án

Đáp án B

Câu 46:

Tìm tổng các nghiệm của phương trình $\log_{2 x - 1} (2 x^{2} + x - 1) + \log_{x + 1} {(2 x - 1)}^{2} = 4$

A. 2

B.

\frac{5}{2}

C.

\frac{15}{4}

D.

\frac{13}{4}

Xem đáp án

Đáp án D

Câu 47:

Tập nghiệm của phương trình $\log_{4} (x + 2) = \log_{2} x$ là

A.

S = \{2; - 1\}

B.

S = \{2;\}

C.

S = \{4\}

D.

S = \{4; - 1\}

Xem đáp án

Đáp án B

Câu 48:

Giải phương trình $\log_{3} x + \log_{3} (x + 2) = 1$ ta được nghiệm

A. x = 3

B. x = 3và x = -1

C.

x = \frac{- 1}{2}

D. x = 3và x = 6

Xem đáp án

Đáp án A

Câu 49:

Tập nghiệm của phương trình $\log (x + 10) + \frac{1}{2} \log x^{2} = 2 - \log 4$ là

A. $S = \{- 5; - 5 + 5 \sqrt{2}\}$

B.

S = \{- 5; - 5 - 5 \sqrt{2}\}

C.

S = \{- 5; - 5 - 5 \sqrt{2}; - 5 + 5 \sqrt{2}\}

D.

S = \{- 5 - 5 \sqrt{2}; - 5 + 5 \sqrt{2}\}

Xem đáp án

Đáp án A

Câu 50:

Tập nghiệm của phương trình $\log_{2} x + \log_{3} x + \log_{4} x = \log_{20} x$ là

A.

S = \{1\}

B.

S = \emptyset

C.

S = \{1; 2\}

D.

S = \{2\}

Xem đáp án

Đáp án A

Câu 51:

Tập nghiệm của phương trình $\log \sqrt{1 + x} + 3 \log \sqrt{1 - x} - 2 = \log \sqrt{1 - x^{2}}$ là

A.

S = \{1\}

B.

S = \emptyset

C.

S = \{1; 2\}

D.

S = \{2\}

Xem đáp án

Đáp án B

Câu 52:

Phương trình $\frac{1}{3} \log_{2} {(3 x - 4)}^{6} . \log_{2} x^{3} = 8 {(\log_{2} \sqrt{x})}^{2} + {(\log_{2} {(3 x - 4)}^{2})}^{2}$ có tập nghiệm là

A.

S = \{1; 2; \frac{16}{9}\}

B.

S = \{1; 2\}

C.

S = \{1; \frac{16}{9}\}

D.

S = \{2; \frac{16}{9}\}

Xem đáp án

Đáp án A

Câu 53:

Tập nghiệm của phương trình $\log_{2 + \sqrt{3}} (x + 1) = \log_{2 - \sqrt{3}} (x + 2)$ là

A. $S = \{\frac{- 3 - \sqrt{5}}{2}\}$

B.

S = \{\frac{- 3 - \sqrt{5}}{2}; \frac{- 3 + \sqrt{5}}{2}\}

C.

S = \{\frac{- 3 + \sqrt{5}}{2}\}

D.

S = \{\frac{3 + \sqrt{5}}{2}\}

Xem đáp án

Đáp án C

Câu 54:

Tập nghiệm của phương trình $\frac{3}{2} \log_{\frac{1}{4}} {(x + 2)}^{2} - 3 = \log_{\frac{1}{4}} {(4 - x)}^{3} + \log_{\frac{1}{4}} {(x + 6)}^{3}$ là

A.

S = \{2\}

B.

S = \{1 - \sqrt{33}\}

C.

S = \{2; 1 + \sqrt{33}\}

D.

S = \{2; 1 - \sqrt{33}\}

Xem đáp án

Đáp án D

Câu 55:

Tìm số nghiệm của phương trình $\log_{2}^{2} x + 3 \log_{2} x + 2 = 0$

A. 2 nghiệm

B. 1 nghiệm

C. Vô nghiệm

D. 3 nghiệm

Xem đáp án

Đáp án A

Câu 56:

Tìm số nghiệm của phương trình

\log_{2}^{2} (x^{2} - 1) + \log_{2} (x - 1) + \log_{2} (x + 1) - 2 = 0

A. 4 nghiệm

B. 1 nghiệm

C. 2 nghiệm

D. 3 nghiệm

Xem đáp án

Đáp án C

Câu 57:

Tìm số nghiệm của phương trình $\log_{2} (x + 1) = \log_{x + 1} 16$

A. Vô nghiệm

B. 3 nghiệm

C. 1 nghiệm

D. 2 nghiệm

Xem đáp án

Đáp án D

Câu 58:

Tìm số nghiệm của phương trình $\log_{x} 2 - \log_{4} x + \frac{7}{6} = 0$

A. 2 nghiệm

B. 1 nghiệm

C. 4 nghiệm

D. 3 nghiệm

Xem đáp án

Đáp án A

Câu 59:

Tìm số nghiệm của phương trình $\log_{3}^{2} x + 5 \sqrt{\log_{3}^{2} x + 1} + 7 = 0$

A. 1 nghiệm

B. Vô nghiệm

C. 2 nghiệm

D. 3 nghiệm

Xem đáp án

Đáp án B

Câu 60:

Tìm số nghiệm của phương trình $\log_{2}^{2} x + \sqrt{\log_{2}^{2} x + 1} = 1$

A. Vô nghiệm

B. 2 nghiệm

C. 1 nghiệm

D. 3 nghiệm

Xem đáp án

Đáp án C

Câu 61:

Tìm số nghiệm của phương trình $\log_{2}^{2} x + (x - 12) \log_{2} x + 11 - x = 0$

A. Vô nghiệm

B. 3 nghiệm

C. 1 nghiệm

D. 2 nghiệm

Xem đáp án

Đáp án D

Câu 62:

Phương trình $\log_{x} (x^{2} + 4 x - 4) = 3$ có số nghiệm là

A. 0

B. 1

C. 2

D. 3

Xem đáp án

Đáp án B

Câu 63:

Giải phương trình $\log_{4} \{2 \log_{3} [1 + \log_{2} (1 + 3 \log_{2} x)]\} = \frac{1}{2}$ ta được nghiệm x = a. Khi đó giá trị a thuộc khoảng nào sau đây?

A. (0;3)

B. (2;5)

C. (5;6)

D. $(6; + \infty)$

Xem đáp án

Đáp án A

Câu 64:

Phương trình

\log_{3} (x^{2} + 4 x + 12) = 2

. Chọn phương án đúng.

A. Có hai nghiệm cùng dương

B. Có hai nghiệm trái dấu

C. Có hai nghiệm cùng âm

D. Vô nghiệm

Xem đáp án

Đáp án C

Câu 65:

Phương trình $x + l o g_{2} (9 - 2^{x}) = 3$ có nghiệm nguyên dương là a. Tính giá trị của biểu thức $T = a^{3} - 5 a - \frac{9}{a^{2}}$

A. T = -7

B. T = 12

C. T = 11

D. T = 6

Xem đáp án

Đáp án C

Câu 66:

Tập nghiệm của phương trình $\log_{2} (2^{x} - 1) = - 2$ là

A.

\{2 - \log_{2} 5\}

B.

\{2 + \log_{2} 5\}

C.

\{\log_{2} 5\}

D.

\{- 2 + \log_{2} 5\}

Xem đáp án

Đáp án D

Câu 67:

Số nghiệm của phương trình $\log_{3} {(x + 1)}^{2} = 2$ là

A. 0

B. 1

C. 2

D. 3

Xem đáp án

Đáp án C

Câu 68:

Tìm m để phương trình $\log_{2} (x^{3} - 3 x) = m$ có ba nghiệm thực phân biệt.

A.

m < 1

B.

0 < m < 1

C.

m > 0

D.

m > 1

Xem đáp án

Đáp án A

Câu 69:

Tìm m để phương trình $\log_{2} (4^{x} - m) = x + 1$ có đúng hai nghiệm phân biệt.

A.

0 < m < 1

B.

0 < m < 2

C.

- 1 < m < 0

D.

- 2 < m < 0

Xem đáp án

Đáp án C

Câu 70:

Nghiệm của phương trình $x + {2.3}^{\log_{2} x} = 3$ là

A. x = 1

B. x = -3; x= 1

C. x = 3,x = 1

D. x = 3

Xem đáp án

Đáp án A

Câu 71:

Tìm tích các nghiệm của phương trình $\log_{3} [{(x + 1)}^{3} + 3 {(x + 1)}^{2} + 3 x + 4] = 2 \log_{2} (x + 1)$

A. -1

B. -7

C. 7

D. 11

Xem đáp án

Đáp án C

Câu 72:

Cho phương trình $\log_{2} (x + 3^{\log_{6} x}) = \log_{6} x$ có nghiệm $x = \frac{a}{b}$ với $\frac{a}{b}$ là phân số tối giản. Khi đó tổng a + b bằng?

A. 1

B. 3

C. 5

D. 7

Xem đáp án

Đáp án A

Câu 73:

Phương trình $2^{\log_{5} (x + 3)} = x$ có bao nhiêu nghiệm?

A. 1

B. 2

C. 3

D. Vô nghiệm

Xem đáp án

Đáp án A

Câu 74:

Gọi Tlà tổng các nghiệm của phương trình $\log_{\frac{1}{3}}^{2} x - 5 \log_{3} x + 6 = 0$ . Tính T

A. T = 36

B. T = -3

C. T = 5

D.

T = \frac{1}{243}

Xem đáp án

Đáp án A

Câu 75:

Phương trình

\log_{3} (\sqrt{x^{2} - 3 x + 2} + 2) + {(\frac{1}{5})}^{3 x - x^{2} - 1} = 2

có tổng các nghiệm bằng?

A. $\sqrt{5}$

B. 3

C. -3

D. $- \sqrt{5}$

Xem đáp án

Đáp án B

Câu 76:

Hiệu của nghiệm lớn nhất với nghiệm nhỏ nhất của phương trình $7^{x - 1} - 2 \log_{7} {(6 x - 5)}^{3} = 1$ là

A. 1

B. 2

C. -1

D. -2

Xem đáp án

Đáp án A

Câu 77:

Phương trình $\log_{3} \frac{2 x + 1}{{(x - 1)}^{2}} = x^{2} - 4 x$ có nghiệm là

A. x = 0

B. x = 0; x= 4

C. Vô nghiệm

D. x = 4

Xem đáp án

Đáp án B

Câu 78:

Phương trình $2^{x - 2 + \sqrt[3]{m - 3 x}} + (x^{3} - 6 x^{2} + 9 x + m) 2^{x - 2} = 2^{x + 1} + 1$ có ba nghiệm phân biệt khi và chỉ khi $m \in (a; b)$ , đặt $T = b^{2} - a^{2}$ thì

A. T = 36

B. T = 64

C. T = 48

D.T = 72

Xem đáp án

Đáp án C

Câu 79:

Nghiệm của phương trình

\frac{x^{3}}{3} + \log_{2} (x + 1) = 11

là

[\begin{array}{l} x = 2 \\ x = 3 \end{array}

A. Vô nghiệm

B. x = 2

C.

[\begin{array}{l} x = 2 \\ x = 3 \end{array}

D. x = 3

Xem đáp án

Đáp án D

Câu 80:

Cho phương trình $e^{m \cos x - \sin x} - e^{2 (1 - \sin x)} = 2 - \sin x - m \cos x$ với mlà tham số thực. Gọi Slà tập các giá trị của mđể phương trình có nghiệm. Khi đó Scó dạng $(- \infty; a] \cup [b; + \infty)$ . Tính $T = 10 a + 20 b$

A. T = 1

B. T = 0

C.

T = 10 \sqrt{3}

D.

T = 3 \sqrt{10}

Xem đáp án

Đáp án C

Câu 81:

Tìm tất cả các giá trị của m để phương trình $x . \log_{2} (x - 1) + m = m . \log_{2} (x - 1) + x$ có hai nghiệm thực phân biệt thuộc $(1; 3]$

A.

m > 3

B.

1 < m < 3

C.

m \neq 3

D. Không có m

Xem đáp án

Đáp án B

Câu 82:

Tìm tất cả các giá trị của tham số m để phương trình $\log_{3}^{2} x - (m + 2) \log_{3} x + 3 m - 1 = 0$ có 2 nghiệm $x_{1} x_{2}$ sao cho $x_{1} x_{2} = 27$

A.

m = \frac{4}{3}

B. m = 25

C.

m = \frac{28}{3}

D. m = 1

Xem đáp án

Đáp án D

Câu 83:

Định điều kiện cho tham số m để $\log_{x} m + \log_{m x} m + \log_{m^{2} x} m = 0$ có nghiệm.

A.

m > 0

B.

\{\begin{cases} m > 0 \\ m \neq 1 \end{cases}

C.

m \neq 1

D.

m > 1

Xem đáp án

Đáp án A

Câu 84:

Số nghiệm của phương trình $\log_{4} x^{2} = \log_{\sqrt{2}} 2$ là

A. 0

B. 1

C. 2

D. 3

Xem đáp án

Đáp án C

Câu 85:

Nghiệm phương trình $\log_{4} (3 x + 4) . \log_{x} 2 = 1$ là

A. x = -2

B. x = 4

C.

[\begin{array}{l} x = - 1 \\ x = 4 \end{array}

D. Vô nghiệm

Xem đáp án

Đáp án A

Câu 86:

Biết rằng phương trình ${[\log_{\frac{1}{3}} (9 x)]}^{2} + \log_{3} \frac{x^{2}}{81} - 7 = 0$ có hai nghiệm phân biệt $x_{1} x_{2}$ . Tính $P = x_{1} x_{2}$

A.

P = \frac{1}{9^{3}}

B.

P = 3^{6}

C.

P = 9^{3}

D.

P = 3^{8}

Xem đáp án

Đáp án A

Câu 87:

Tìm tập nghiệm S của phương trình $\log_{\sqrt{2}} (x - 1) + \log_{\frac{1}{2}} (x + 1) = 1$ .

A. $S = \{\frac{3 + \sqrt{13}}{2}\}$

B.

S = \{3\}

C.

S = \{2 - \sqrt{5}; 2 + \sqrt{5}\}

D.

S = \{2 + \sqrt{5}\}

Xem đáp án

Đáp án D

Câu 88:

Biết rằng phương trình $\log_{3} (3^{x + 1} - 1) = 2 x + \log_{\frac{1}{3}} 2$ có hai nghiệm $x_{1}$ và $x_{2}$ . Hãy tính tổng $S = 27^{x_{1}} + 27^{x_{2}}$

A. S = 180

B. S = 45

C. S = 9

D. S = 252

Xem đáp án

Đáp án A

Câu 89:

Số nghiệm của phương trình $\frac{x^{3} - 5 x^{2} + 6 x}{\ln (x - 1)} = 0$ là

A. 0

B. 1

C. 2

D. 3

Xem đáp án

Đáp án B

Câu 90:

Biết rằng phương trình $2 \log_{2} x + \log_{\frac{1}{2}} (1 - \sqrt{x}) = \frac{1}{2} \log_{\sqrt{2}} (x - 2 \sqrt{x} + 2)$ có nghiệm duy nhất dạng $a + b \sqrt{3}$ với $a, b \in ℤ$ . Tính tổng S = a + b

A. S = 6

B. S = 2

C. S = -2

D. S = -6

Xem đáp án

Đáp án B

Câu 91:

Phương trình $\log_{3} \frac{x^{2} - 2 x + 1}{x} + x^{2} + 1 = 3 x$ có tổng các nghiệm bằng:

A. 3

B. 5

C.

\sqrt{5}

D. 2

Xem đáp án

Đáp án A

Câu 92:

Gọi S là tổng các giá trị nguyên của tham số m sao cho phương trình $\log_{4} (2^{2 x} + 2^{x + 2} + 2^{2}) = \log_{2} |m - 2|$ vô nghiệm. Giá trị của S bằng

A. S = 6

B. S = 8

C. S = 10

D. S = 12

Xem đáp án

Đáp án C

Câu 93:

Tìm các giá trị thực của tham số m để phương trình $\frac{\log (m x) - 2}{\log (x + 1)} = 1$ có nghiệm duy nhất

A. $0 < m < 100$

B.

m < 0; m > 100

C. m = 1

D. Không tồn tại m

Xem đáp án

Đáp án B

Câu 94:

Tìm các giá trị thực của tham số m để phương trình $\frac{\log (m x) - 2}{\log (x + 1)} = 1$ có nghiệm duy nhất

A. $0 < m < 100$

B.

m < 0; m > 100

C. m = 1

D. Không tồn tại m

Xem đáp án

Đáp án B

Câu 95:

Tìm giá trị thực của tham số m để phương trình $\log_{\sqrt{3}}^{2} x - m \log_{\sqrt{3}} x + 1 = 0$ có nghiệm duy nhất nhỏ hơn 1.

A. m = 2

B. m = -2

C.

m = \sqrt{2}

D. m = 0

Xem đáp án

Đáp án B

Câu 96:

Gọi $m_{0}$ là giá trị thực nhỏ nhất của tham số m sao cho phương trình $(m - 1) \log_{\frac{1}{2}}^{2} (x - 2) - (m - 5) \log_{\frac{1}{2}} (x - 2) + m - 1 = 0$ có nghiệm thuộc (2;4). Mệnh đề nào sau đây là đúng?

A.

m \in (- 5; - \frac{5}{2})

B.

m \in (- 1; \frac{4}{3})

C.

m \in (2; \frac{10}{3})

D.Không tồn tại m

Xem đáp án

Đáp án A

Câu 97:

Tìm các giá trị thực của tham số m để phương trình $\frac{\log (m x) - 2}{\log (x + 1)} = 1$ có nghiệm duy nhất

A. $0 < m < 100$

B.

m < 0; m > 100

C. m = 1

D. Không tồn tại m

Xem đáp án

Đáp án B

Câu 98:

Cho phương trình $\sqrt{\log_{2}^{2} x - 2 \log_{2} x - 3} = m (\log_{2} x - 3)$ với m là tham số thực. Tìm các giá trị của m để phương trình có nghiệm thuộc $[16; + \infty)$

A. $1 < m \leq 2$

B. $1 < m \leq \sqrt{5}$

C. $\frac{3}{4} \leq m \leq \sqrt{5}$

D. $1 \leq m \leq \sqrt{5}$

Xem đáp án

Đáp án B

Câu 99:

Có bao nhiêu giá trị m nguyên thuộc $[- 2017; 2017]$ để phương trình $\log (m x) = 2 \log (x + 1)$ có nghiệm duy nhất?

A. 2017

B. 4014

C. 2018

D. 4015

Xem đáp án

Đáp án C

Câu 100:

Tìm các giá trị của tham số m để phương trình $\log_{2} \frac{4^{x} - 1}{4^{x} + 1} - m = 0$ có nghiệm.

A.

m < 0

B.

- 1 < m < 1

C.

m \leq - 1

D.

- 1 < m < 0

Xem đáp án

Đáp án A

Câu 101:

Cho phương trình $2^{{(x - 1)}^{2}} . \log_{2} (x^{2} - 2 x + 3) = 4^{|x - m|} . \log_{2} (2 |x - m| + 2)$ với m là tham số thực. Tìm tất cả các giá trị của m để phương trình có đúng hai nghiệm phân biệt.

A. $m \in (- \infty; \frac{1}{2}) \cup (\frac{3}{2}; + \infty)$

B.

m \in (- \infty; \frac{1}{2}] \cup [\frac{3}{2}; + \infty)

C.

m \in (- \infty; - 1] \cup [1; + \infty)

D.

m \in (- \infty; 1) \cup (1; + \infty)

Xem đáp án

Đáp án A

Câu 102:

Cho phương trình $\log_{3} (x^{2} + 4 m x) + \log_{\frac{1}{3}} (2 x - 2 m - 1) = 0$ với m là tham số thực. Gọi Slà tập tất cả các giá trị của mmđể phương trình có nghiệm duy nhất, khi đó Scó dạng $[a; b] \cup \{c\}$ với $a < b < c$ . Tính $P = 2 a + 10 b + c$

A. P = 0

B. P = 15

C. P = -2

D. P = 13

Xem đáp án

Đáp án C

Câu 103:

Tập nghiệm của bất phương trình $\log_{3} (\log_{\frac{1}{2}} x) \geq 0$ có dạng $S = (a; \frac{b}{c}]$ , với $\frac{b}{c}$ là phân số tối giản và alà số nguyên. Tính a + b + c

A. 3

B. 2

C. -2

D. 6

Xem đáp án

Ta có: $\log_{3} (\log_{\frac{1}{2}} x) \geq 0 \Leftrightarrow \log_{\frac{1}{2}} x \geq 1 \Leftrightarrow 0 < x \leq \frac{1}{2}$

Nên $a = 0, b = 1, c = 2$ , do đó $a + b + c = 3$

Chọn A.

Câu 104:

Tập nghiệm của bất phương trình $\log_{\frac{1}{2}} [\log_{2} (2 - x^{2})] > 0$ là $S = (a; b) \ \{0\}$ . Tính a + 3b

A. 3

B. 2

C. -2

D. 0

Xem đáp án

Ta có: $\log_{\frac{1}{2}} [\log_{2} (2 - x^{2})] > 0 \Leftrightarrow 0 < \log_{2} (2 - x^{2}) < 1 \Leftrightarrow 1 < 2 - x^{2} < 2$

$\Leftrightarrow \{\begin{cases} x^{2} < 1 \\ x^{2} > 0 \end{cases} \Leftrightarrow \{\begin{cases} - 1 < x < 1 \\ x \neq 0 \end{cases}$ . Nên $a = - 1; b = 1$ . Do đó $a + 3 b = 2$

Chọn B.

Câu 105:

Tìm số nghiệm nguyên của bất phương trình $\log_{\frac{2}{3}} [\log_{3} |x - 3|] \geq 0$

A. 7

B. 4

C. 6

D. 5

Xem đáp án

Điều kiện: $\{\begin{cases} x \neq 3 \\ \log_{3} |x - 3| > 0 \end{cases} \Leftrightarrow \{\begin{cases} x \neq 3 \\ |x - 3| > 1 \end{cases} \Leftrightarrow [\begin{array}{l} x > 4 \\ x < 2 \end{array}$

Ta có: $\log_{\frac{2}{3}} [\log_{3} |x - 3|] \geq 0 \Leftrightarrow 0 < \log_{3} |x - 3| \leq 1 \Leftrightarrow \{\begin{cases} |x - 3| \leq 3 \\ |x - 3| > 1 \end{cases}$

$\Leftrightarrow \{\begin{cases} 1 < x - 3 \leq 3 \\ - 1 > x - 3 \geq - 3 \end{cases} \Leftrightarrow \{\begin{cases} 4 < x \leq 6 \\ 2 > x \geq 0 \end{cases} \Leftrightarrow x \in [0; 2) \cup (4; 6]$

Vậy số nghiệm nguyên của bất phương trình là 4

Chọn B.

Câu 106:

Bất phương trình $\max \{\log_{3} x, \log_{\frac{1}{2}} x\} < 3$ có tập nghiệm là

A.

(- \infty; 27)

B.

(8; 27)

C.

(\frac{1}{8}; 27)

D.

(27; + \infty)

Xem đáp án

Điều kiện: $x > 0$

Ta có $\max \{\log_{3} x, \log_{\frac{1}{2}} x\} < 3 \Leftrightarrow \{\begin{cases} \log_{3} x < 3 \\ \log_{\frac{1}{2}} x < 3 \end{cases} \Leftrightarrow \{\begin{cases} x < 27 \\ x > \frac{1}{8} \end{cases} \Leftrightarrow \frac{1}{8} < x < 27$

Vậy tập nghiệm của bất phương trình là: $S = (\frac{1}{8}; 27)$

Chọn C.

Câu 107:

Số nghiệm nguyên của bất phương trình $\log_{\sqrt{2}}^{2} (2 x) - 2 \log_{2} (4 x^{2}) - 8 \leq 0$ là

A. Vô số

B. 2

C. 0

D. 1

Xem đáp án

Ta có:

$\log_{\sqrt{2}}^{2} (2 x) - 2 \log_{2} (4 x^{2}) - 8 \leq 0$

$\Leftrightarrow 4 \log_{2}^{2} (2 x) - 4 \log_{2} (2 x) - 8 \leq 0$

$\Leftrightarrow - 1 \leq \log_{2} (2 x) \leq 2 \Leftrightarrow \frac{1}{2} \leq 2 x \leq 4 \Leftrightarrow \frac{1}{4} \leq x \leq 2$

Bất phương trình có 2 nghiệm nguyên.

Chọn B.

Câu 108:

Tập nghiệm của bất phương trình $\frac{1}{2 - \ln x} + \frac{1}{\ln x} > 2$ là $S = (a; e^{b}) \ \{e^{c}\}$ , với $a, b, c \in ℤ$ . Tính $a + b + c$

A. 3

B. 2

C. 4

D. 6

Xem đáp án

Tập nghiệm của bất phương trình 1/ 2- ln x + 1/ ln x lớn hơn 2 là S= (a; e^b) (ảnh 1)

Chọn C.

Câu 109:

Số nghiệm nguyên của bất phương trình

\log_{3} x + \log_{3 x} 3^{6} \leq 3

là

A. 9

B. 0

C. 11

D. 5

Xem đáp án

Ta có: $\log_{3} x + \frac{1}{\log_{3^{6}} 3 x} < 3 \Leftrightarrow \log_{3} x + \frac{6}{1 + \log_{3} x} - 3 < 0$

$\Leftrightarrow \frac{\log_{3}^{2} x - 2 \log_{3} x + 3}{\log_{3} x + 1} \leq 0 \Leftrightarrow \log_{3} x + 1 < 0$ vì $\log_{3}^{2} x - 2 \log_{3} x + 3 > 0, \forall x > 0$

$\Leftrightarrow \log_{3} x < - 1 \Leftrightarrow 0 < x < \frac{1}{3}$ nên không có giá trị nguyên thỏa mãn bài toán.

Chọn B.

Câu 110:

Bất phương trình $\log_{\frac{2}{3}} (2 x^{2} - x - 1) > 0$ có tập nghiệm là $(a; b) \cup (c; d)$ . Tính tổng a + b + c + d

A.

\frac{3}{2}

B. 0

C. 1

D.

- \sqrt{17}

Xem đáp án

Bất phương trình log 2/3 ( 2x^2 - x - 1) lớn hơn 0 có tập nghiệm là (ảnh 1)

Chọn C

Câu 111:

Bất phương trình

x^{- 2 + \log x} < 1000

có tất cả bao nhiêu nghiệm nguyên?

A. 999

B. 1000

C. Vô số

D. 1001

Xem đáp án

Bất phương trình x^ -2 + log x nhỏ hơn 1000 có tất cả bao nhiêu nghiệm nguyên? (ảnh 1)

Chọn A.

Câu 112:

Biết tập nghiệm S của bất phương trình $\log_{\frac{π}{6}} [\log_{3} (x - 2)] > 0$ là khoảng (a;b). Tính b - a

A. 2

B. 4

C. 3

D. 5

Xem đáp án

Điều kiện: $\{\begin{cases} x - 2 > 0 \\ \log_{3} (x - 2) > 0 \end{cases} \Leftrightarrow \{\begin{cases} x > 2 \\ x - 2 > 1 \end{cases} \Leftrightarrow \{\begin{cases} x > 2 \\ x > 3 \end{cases} \Leftrightarrow x > 3$

$\log_{\frac{π}{6}} [\log_{3} (x - 2)] > 0 \Leftrightarrow \log_{3} (x - 2) < 1 \Leftrightarrow x - 2 < 3 \Leftrightarrow x < 5$

So với điều kiện, tập nghiệm bất phương trình $S = (3; 5)$

Do đó: $b - a = 5 - 3 = 2$

Chọn A.

Câu 113:

Có bao nhiêu giá trị nguyên $x \in (0; 30)$ thỏa mãn bất phương trình $\log_{\frac{1}{3}}^{2} x - 5 \log_{3} x + 6 > 0$ ?

A. 9

B. 10

C. 26

D. 27

Xem đáp án

Có bao nhiêu giá trị nguyên x thuộc (0;30) thỏa mãn bất phương trình log 1/3 x^2 - 5 log 3x + 6 lớn hơn 0 ? (ảnh 1)

Chọn B.

Câu 114:

Tìm tập nghiệm S của bất phương trình

\frac{\log_{2} \frac{x}{2}}{\log_{2} x} - \frac{\log_{2} x^{2}}{\log_{2} x - 1} \leq 1

A. $(0; \frac{1}{2}] \cup (1; \sqrt{2}] \cup (2; + \infty)$

B.

(0; \frac{1}{2}] \cup (1; \sqrt{2}]

C.

(0; \frac{1}{2}] \cup [\sqrt{2}; + \infty)

D.

(0; \frac{1}{2}] \cup [1; + \infty)

Xem đáp án

Tìm tập nghiệm S của bất phương trình log 2 x/2 / log 2 x - log 2 x^2/ log 2x - 1 nhỏ hơn hoặc bằng 1 (ảnh 1)

Chọn A.

Câu 115:

Biết rằng bất phương trình $\log_{2} (5^{x} + 2) + 2. \log_{(5^{x} + 2)} 2 > 3$ có tập nghiệm là $S = (\log_{a} b; + \infty)$ , với a,b là các số nguyên dương nhỏ hơn 6 và $a \neq 1$ . Tính $P = 2 a + 3 b$

A. P = 11

B. P = 16

C. P = 18

D. P = 7

Xem đáp án

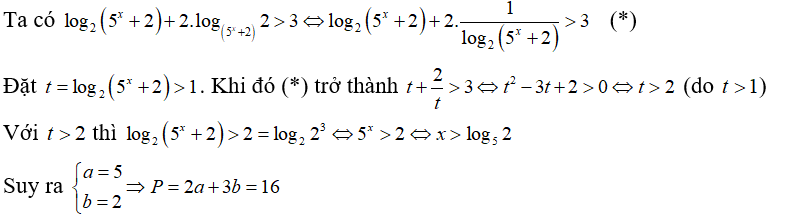
Biết rằng bất phương trình log 2( 5^x +2) + 2. log (5 ^x +2) 2 lớn hơn hoặc bằng 3 có tập nghiệm là (ảnh 1)

Chọn B.

Câu 116:

Tập nghiệm của bất phương trình $\log_{4} (x - 1) . \log_{5} (x + 1) \leq \log_{20} (x - 1)$ có dạng là $S = [a^{\log_{a b} b} - c; d]$ với a,b,c,dlà các số nguyên dương. Tính tổng a + b + c + d

A. 11

B. 13

C. 12

D. 5

Xem đáp án

Tập nghiệm của bất phương trình log 4( x -1) log 5( x +1) nhỏ hơn hoặc bằng log 20 (x - 1) có dạng là (ảnh 1)

Chọn C.

Câu 117:

Có bao nhiêu giá trị nguyên của tham số $m \in (- 10; 10)$ để bất phương trình $4 {(\log_{2} \sqrt{x})}^{2} + \log_{2} x + m \geq 0$ nghiệm đúng với mọi $x \in (1; 64)$

A. 8

B. 11

C. 10

D. 9

Xem đáp án

Có bao nhiêu giá trị nguyên của tham số x thuộc -10; 10 để bất phương trình 4( log 2 căn x)^ 2 + log 2x + m lớn hơn hoặc bằng 0 nghiệm đúng với mọi (ảnh 1)

Chọn D.

Câu 118:

Có bao nhiêu giá trị nguyên của tham số $m \in (- 10; 10)$ để bất phương trình $\ln^{2} x - m \ln x + m + 3 \leq 0$ nghiệm đúng với mọi $x > 3$

A. 6

B. 4

C. 1

D. 0

Xem đáp án

Có bao nhiêu giá trị nguyên của tham số m thuộc -10;10 để bất phương trình ln^2x - mln x + m + 3 nhỏ hơn hoặc bằng 0 (ảnh 1)

Chọn B.

Câu 119:

Số giá trị nguyên của tham số m để bất phương trình $\log 5 + \log (x^{2} + 1) \geq \log (m x^{2} + 4 x + m)$ nghiệm đúng với mọi x là

A. 2

B. 4

C. 1

D. 0

Xem đáp án

Số giá trị nguyên của tham số m để bất phương trình log 5 + log( x^2 + 1) lớn hơn hoặc bằng log( mx^2 + 4x +m) nghiệm đúng với mọi (ảnh 1)

Chọn A.

Câu 120:

Giải bất phương trình

\log_{2} (3 x - 2) > \log_{2} (6 - 5 x)

được tập nghiệm là (a,b). Hãy tính tổng

S = a + b

A.

S = \frac{26}{5}

B.

S = \frac{11}{5}

C.

S = \frac{28}{15}

D.

S = \frac{8}{3}

Xem đáp án

Đáp án B

Câu 121:

Tìm tập nghiệm của bất phương trình $\log_{\frac{π}{4}} (x^{2} - 1) < \log_{\frac{π}{4}} (3 x - 3)$

A. $S = (1; 2)$

B.

S = (- \infty; - 1) \cup (2; + \infty)

C.

S = (- \infty; 1) \cup (2; + \infty)

D.

S = (2; + \infty)

Xem đáp án

Đáp án D

Câu 122:

Bất phương trình

\log_{\frac{1}{2}} (2 x - 1) > \log_{\frac{1}{2}} (x + 2)

có tập nghiệm là

A.

(3; + \infty)

B.

(- \infty; 3)

C.

(\frac{1}{2}; 3)

D.

(- 2; 3)

Xem đáp án

Đáp án C

Câu 123:

Tập nghiệm của bất phương trình $\log_{0,8} (x^{2} + x) < \log_{0,8} (- 2 x + 4)$ là

A.

(- \infty; - 4) \cup (1; + \infty)

B.

(- 4; 1)

C.

(- \infty; - 4) \cup (1; 2)

D. ( 1;2)

Xem đáp án

Đáp án C

Câu 124:

Tìm tập nghiệm S của bất phương trình

Tìm tập nghiệm của bất phương trình (ảnh 1)

A. $S = (0; \frac{1}{3}) \cup (1; + \infty)$

B. $S = (- \infty; \frac{1}{3}) \cup (1; + \infty)$

C. $S = (\frac{1}{3}; 1)$

D. $S = [0; \frac{1}{3}) \cup (1; + \infty)$

Xem đáp án

Đáp án A

Câu 125:

Tập nghiệm của bất phương trình $\ln (x^{2} - 3 x + 2) \geq \ln (5 x + 2)$ là

A. $(- \infty; 0] \cup [8; + \infty)$

B.

[0; 1) \cup (2; 8]

C.

(- \frac{2}{5}; 0] \cup [8; + \infty)

D.

[8; + \infty)

Xem đáp án

Đáp án C

Câu 126:

Bất phương trình

\log_{4} (x + 7) > \log_{2} (x + 1)

có tập nghiệm là

A. (1;4)

B. (-1;2)

C.

(5; + \infty)

D.

(- \infty; 1)

Xem đáp án

Đáp án B

Câu 127:

Tập nghiệm của bất phương trình $\log_{3} x < \log_{\sqrt{3}} (12 - x)$ là

A. (0;12)

B. (9;16)

C. (0;9)

D. (0;16)

Xem đáp án

Đáp án C

Câu 128:

Với m là tham số thực dương khác 1. Hãy tìm tập nghiệm S của bất phương trình $\log_{m} (2 x^{2} + x + 3) \leq \log_{m} (3 x^{2} - x)$ , biết rằng x= 1 là một nghiệm của bất phương trình.

A. $S = (- 2; 0) \cup (\frac{1}{3}; 3]$

B.

S = (- 1; 0) \cup (\frac{1}{3}; 2]

C.

S = [- 1; 0) \cup (\frac{1}{3}; 3]

D.

S = (- 1; 0) \cup (1; 3]

Xem đáp án

Đáp án C

Câu 129:

Tập xác định của hàm số $y = \sqrt{\ln (x - 1) + \ln (x + 1)}$ là

A.

(1; + \infty)

B.

(- \infty; \sqrt{2})

C.

\emptyset

D.

[\sqrt{2}; + \infty)

Xem đáp án

Đáp án D

Câu 130:

Bất phương trình $\log_{\frac{3}{2}} x \leq \log_{\frac{9}{4}} (x - 1)$ tương đương với bất phương trình nào sau đây?

A. $\log_{\frac{3}{2}} x \leq \log_{\frac{9}{4}} x - \log_{\frac{9}{4}} 1$

B.

2 \log_{\frac{3}{2}} x \leq \log_{\frac{3}{2}} (x - 1)

C.

\log_{\frac{9}{4}} x \leq \log_{\frac{3}{2}} (x - 1)

D.

\log_{\frac{3}{2}} x \leq 2 \log_{\frac{3}{2}} (x - 1)

Xem đáp án

Đáp án B

Câu 131:

Tất cả các giá trị của m để bất phương trình $\log_{2} (7 x^{2} + 7) \geq \log_{2} (m x^{2} + 4 x + m)$ có nghiệm đúng với mọi giá trị của x là

A.

m \leq 5

B.

2 < m \leq 5

C.

m \geq 7

D.

2 \leq m \leq 5

Xem đáp án

Đáp án B

Câu 132:

Có bao nhiêu số nguyên dương x thỏa mãn điều kiện $\log (x - 40) + \log (60 - x) < 2$ ?

A. 20

B. 18

C. 21

D. 19

Xem đáp án

Đáp án B

Câu 133:

Tập nghiệm của bất phương trình $2 \log_{2} (x - 1) \leq \log_{2} (5 - x) + 1$ là

A. (1;5)

B. [1;3]

C. (1;3]

D. [3;5]

Xem đáp án

Đáp án C

Câu 134:

Bất phương trình $2 \log_{3} (4 x - 3) + \log_{\frac{1}{3}} (2 x + 3) \leq 2$ là

A.

[\frac{3}{4}; + \infty)

B.

(\frac{3}{4}; + \infty)

C.

(\frac{3}{4}; 3]

D.

[\frac{3}{4}; 3]

Xem đáp án

Đáp án C

Câu 135:

Bất phương trình $\log_{2} x + \log_{3} x + \log_{4} x > \log_{20} x$ có tập nghiệm là

A.

[1; + \infty)

B.

(0; 1]

C.

(0; 1)

D.

(1; + \infty)

Xem đáp án

Đáp án D

Câu 136:

Tập nghiệm của bất phương trình $\log_{2} (x + 2) - \log_{2} (x - 2) < 2$ là

A.

(\frac{10}{3}; + \infty)

B.

(- 2; + \infty)

C.

(2; + \infty)

D. (-2;2)

Xem đáp án

Đáp án A

Câu 137:

Tập nghiệm của bất phương trình $\log (x^{2} + 2 x - 3) + \log (x + 3) - \log (x - 1) < 0$ là

A.

(- 4; - 2) \cup (1; + \infty)

B.

(- 2; 1)

C.

(1; + \infty)

D.

\emptyset

Xem đáp án

Đáp án D

Câu 138:

Bất phương trình $\log_{2} (2 x - 1) - \log_{\frac{1}{2}} (x - 2) \leq 1$ có tập nghiệm là

A.

(2; + \infty)

B.

(2; 3]

C.

(2; \frac{5}{2}]

D.

[\frac{5}{2}; 3]

Xem đáp án

Đáp án C

Câu 139:

Tìm tập nghiệm S của bất phương trình

\log_{\frac{1}{2}} (x + 2) - \log_{\frac{1}{\sqrt{2}}} (x) > \log_{2} (x^{2} - x) - 1

.

A.

S = (2; + \infty)

B.

S = (1; 2)

C.

S = (0; 2)

D.

S = (1; 2]

Xem đáp án

Đáp án B

Câu 140:

Cho bất phương trình $\log_{0,2} x - \log_{5} (x - 2) < \log_{0,2} 3$ . Nghiệm của bất phương trình đã cho là

A.

x > 3

B.

2 \leq x < 3

C.

x \geq 2

D.

2 < x < 3

Xem đáp án

Đáp án A

Câu 141:

Cho bất phương trình $\log_{0,2} x - \log_{5} (x - 2) < \log_{0,2} 3$ . Nghiệm của bất phương trình đã cho là

A.

x > 3

B.

2 \leq x < 3

C.

x \geq 2

D.

2 < x < 3

Xem đáp án

Đáp án A

Câu 142:

Số nghiệm nguyên của bất phương trình

\log_{\frac{1}{2}} x + \log_{\frac{1}{2}} (x + \frac{1}{2}) \geq 1

là

A. Vô số

B. 0

C. 2

D. 3

Xem đáp án

Đáp án B

Câu 143:

Tập nghiệm của bất phương trình $\log (x + 1) + \log x > \log 20$ là

A. (-5;4)

B.

(- \infty; - 5)

C.

(- \infty; - 5) \cup (4; + \infty)

D.

(4; + \infty)

Xem đáp án

Đáp án D

Câu 144:

Tập nghiệm của bất phương trình $\log_{2} (x + 1) - 2 \log_{2} (5 - x) < 1 - \log_{2} (x - 2)$ chứa khoảng nào dưới đây?

A. (1;2)

B. (-4;3)

C. (2;3)

D. (-2;5)

Xem đáp án

Đáp án C

Câu 145:

Bất phương trình $3 \log_{3} (x - 1) + \log_{\sqrt[3]{3}} (2 x - 1) \leq 3$ có tập nghiệm là

A. (1;2]

B. [1;2]

C.

[- \frac{1}{2}; 2]

D.

(- \frac{1}{2}; 2]

Xem đáp án

Đáp án A

Câu 146:

Nghiệm của bất phương trình $\log_{5} x^{3} + \log_{0,2} x + \log_{\sqrt[3]{25}} x \leq 7$ là

A.

x \leq 25

B.

0 < x \leq 25

C.

x \geq 10

D.

0 < x \leq 10

Xem đáp án

Đáp án B

Câu 147:

Nghiệm của bất phương trình $2 \log_{2} \sqrt{x + 1} \leq 2 - \log_{2} (x - 2)$ là

A.

2 < x \leq 3

B.

x < - 2

C.

3 < x

D.

- 2 < x < 3

Xem đáp án

Đáp án A

Câu 148:

Nghiệm của bất phương trình $\log_{2} (\sqrt{3 x + 1} + 6) - 1 \geq \log_{2} (7 - \sqrt{10 - x})$ là

A.

x \leq 1

B.

x \leq \frac{369}{49}

C.

x \geq \frac{369}{49}

D.

1 \leq x \leq \frac{369}{49}

Xem đáp án

Đáp án D

Câu 149:

Nghiệm của bất phương trình $\log_{3} \sqrt{x^{2} - 5 x + 6} + \log_{\frac{1}{3}} \sqrt{x - 2} < \frac{1}{2} \log_{\frac{1}{3}} (x + 3)$ là

A.

x > 5

B.

x > 3

C.

3 < x < 4

D.

x > \sqrt{10}

Xem đáp án

Đáp án C

Câu 150:

Giá trị nào của tham số m thì bất phương trình $\log_{2} (3 x^{2} - 2 m x - m^{2} - 2 m + 4) > 1 + \log_{2} (x^{2} + 2)$ nghiệm đúng với mọi $x \in ℝ$ ?

A.

m < - 1 \lor m > 0

B.

- 1 < m < 0

C.

m > 0

D.

m < - 1

Xem đáp án

Đáp án B

Câu 151:

Tập nghiệm S của bất phương trình $\log_{2}^{2} x - 5 \log_{2} x - 6 \leq 0$ là

A. $S = [\frac{1}{2}; 64]$

B.

S = (0; \frac{1}{2}]

C.

S = [64; + \infty)

D.

S = (0; \frac{1}{2}] \cup [64; + \infty)

Xem đáp án

Đáp án A

Câu 152:

Nghiệm của bất phương trình $\log_{2}^{2} x - 6 \log_{2} x > - 5$ là

A.

[\begin{array}{l} x > 32 \\ x < 1 \end{array}

B.

[\begin{array}{l} x > 5 \\ x < 1 \end{array}

C.

[\begin{array}{l} x > 32 \\ 0 < x < 2 \end{array}

D.

[\begin{array}{l} x \geq 32 \\ x \leq 1 \end{array}

Xem đáp án

Đáp án C

Câu 153:

Tìm tập nghiệm S của bất phương trình

\log_{2}^{2} (2 - x) + 4 \log_{2} (2 - x) \geq 5

A. $S = (- \infty; 0] \cup [\frac{63}{32}; 2)$

B.

S = (- \infty; 0] \cup [\frac{63}{32}; + \infty)

C.

S = [2; + \infty)

D.

S = (- \infty; 0]

Xem đáp án

Đáp án A

Câu 154:

Nghiệm của bất phương trình ${(\ln x)}^{2} - 2 \ln x > - 1$ là

A.

\{\begin{cases} x \neq e \\ x > 0 \end{cases}

B.

x \neq 1

C.

x \in ℝ \ \{1\}

D.

x \in ℝ

Xem đáp án

Đáp án A

Câu 155:

Nghiệm của bất phương trình $\log_{2}^{2} - 3 \log_{2} x \leq - 2$ là

A.

1 < x < 2

B.

2 < x < 4

C.

2 \leq x \leq 4

D.

1 \leq x \leq 2

Xem đáp án

Đáp án C

Câu 156:

Tập nghiệm của bất phương trình $\ln^{2} x - 3 \ln x + 2 \geq 0$ là

A.

(- \infty; 1] \cup [2; + \infty)

B.

[e^{2}; + \infty)

C.

(- \infty; e] \cup [e^{2}; + \infty)

D.

(0; e] \cup [e^{2}; + \infty)

Xem đáp án

Đáp án D

Câu 157:

Tập nghiệm của bất phương trình $\log_{3} \frac{3}{x} . \log_{3} x - \log_{3} \frac{x^{3}}{\sqrt{3}} > \frac{1}{2} + 2 \log_{3} \sqrt{x}$ là

A.

(0; + \infty)

B.

(0; \frac{\sqrt{3}}{8}) \cup (1; + \infty)

C.

(\frac{\sqrt{3}}{8}; 1)

D.

(\frac{1}{27}; 1)

Xem đáp án

Đáp án D

Câu 158:

Tập nghiệm của bất phương trình $\log_{2}^{2} x - 6 \log_{4} x - 4 < 0$ là

A. $(\frac{1}{2}; 16)$

B.

(- 1; 4)

C.

(- 1; 16)

D.

(\frac{1}{2}; 4)

Xem đáp án

Đáp án A

Câu 159:

Tập xác định của hàm số

y = \sqrt{\ln^{2} x - 3 \ln x + 2}

là

A.

(0; e] \cup [e^{2}; + \infty)

B.

(- \infty; 1] \cup [2; + \infty)

C.

(- \infty; e] \cup [e^{2}; + \infty)

D.

[e^{2}; + \infty)

Xem đáp án

Đáp án A

Câu 160:

Tìm tập nghiệm S của bất phương trình $\log_{\sqrt{2}}^{2} (2 x) - 2 \log_{2} (4 x^{2}) - 8 \leq 0$

A.

S = [\frac{1}{4}; 2]

B.

S = (- \infty; 2]

C.

S = [- 2; 2]

D.

S = (0; 2]

Xem đáp án

Đáp án A

Câu 161:

Tập nghiệm của bất phương trình $\log_{\sqrt{2}}^{2} x - 10 \log_{2} \sqrt{x} + 1 > 0$ là

A.

(2; + \infty)

B.

(- \infty; 2^{\frac{1}{4}}) \cup (2; + \infty)

C.

(0; 2^{\frac{1}{4}}) \cup (2; + \infty)

D.

(0; 2^{\frac{1}{4}})

Xem đáp án

Đáp án C

Câu 162:

Tập nghiệm của bất phương trình $\log_{2}^{2} x + 9 \log_{8} x \geq \frac{5}{2} \log_{4 \sqrt{2}} 16$ là

A.

[\frac{1}{16}; 2)

B.

(0; \frac{1}{16}] \cup [2; + \infty)

C.

[\frac{1}{16}; + \infty)

D.

[2; + \infty)

Xem đáp án

Đáp án B

Câu 163:

Tập nghiệm của bất phương trình $\log_{2}^{2} (2 - x) - 8 \log_{0,25} (2 - x) - 5 \geq 0$ là

A.

(- \infty; 0] \cup [\frac{63}{32}; 2)

B.

(- \infty; \frac{63}{32}]

C.

(- \infty; - 5] \cup [1; + \infty)

D.

(- \infty; 2)

Xem đáp án

Đáp án A

Câu 164:

Tập nghiệm của bất phương trình

\log_{\sqrt{2}}^{2} x - 5 \log_{2} x + 1 < 0

là

A.

(2^{\frac{1}{4}}; 2)

B.

(0; 2^{\frac{1}{4}}) \cup (2; + \infty)

C.

(2; + \infty)

D.

(0; 2)

Xem đáp án

Đáp án A

Câu 165:

Cho bất phương trình $\log_{4} x . \log_{2} (4 x) + \log_{\sqrt{2}} (\frac{x^{3}}{2}) < 0$ . Nếu đặt $t = \log_{2} x$ , ta được bất phương trình nào sau đây?

A.

t^{2} + 11 t - 2 < 0

B.

t^{2} + 11 t - 3 < 0

C.

t^{2} + 14 t - 2 < 0

D.

t^{2} + 14 t - 4 < 0

Xem đáp án

Đáp án D

Câu 166:

Tổng các nghiệm nguyên của bất phương trình $\log_{3}^{2} x^{5} - 25 \log_{3} x^{2} - 750 \leq 0$ là

A. 925480

B. 38556

C. 378225

D. 388639

Xem đáp án

Đáp án A

Câu 167:

Tập nghiệm của bất phương trình $\log_{4} (3^{x} - 1) . \log_{\frac{1}{4}} \frac{3^{x} - 1}{16} \leq \frac{3}{4}$ là

A. $(1; 2] \cup [3; + \infty)$

B.

(- 1; 1] \cup [4; + \infty)

C.

(0; 4] \cup [5; + \infty)

D.

(0; 1] \cup [2; + \infty)

Xem đáp án

Đáp án D

Câu 168:

Bất phương trình $2 \log_{\frac{2}{3}} x . \log_{\frac{3}{2}} x + 2 \log_{\frac{2}{3}} x - 4 \log_{\frac{3}{2}} x - 4 > 0$ có nghiệm là

A.

x < \frac{2}{3}

B.

x < \frac{4}{9}

C.

x > \frac{4}{9}

D.

\frac{4}{9} < x < \frac{2}{3}

Xem đáp án

Đáp án D

Câu 169:

Bất phương trình $\log_{4} x - \log_{x} 4 \leq - \frac{3}{2}$ có bao nhiêu nghiệm nguyên trên đoạn $[1; 5]$

A. 1

B. 2

C. 3

D. 4

Xem đáp án

Đáp án A

Câu 170:

Nghiệm của bất phương trình $\log_{x} 100 - \frac{1}{2} \log_{100} x > 0$ là

A.

1 < x < 10^{2 \sqrt{2}}

B.

[\begin{array}{l} x < \frac{1}{10^{2 \sqrt{2}}} \\ 1 < x < 10^{2 \sqrt{2}} \end{array}

C.

0 < x < \frac{1}{10^{2 \sqrt{2}}}

D.

[\begin{array}{l} 0 < x < \frac{1}{10^{2 \sqrt{2}}} \\ 1 < x < 10^{2 \sqrt{2}} \end{array}

Xem đáp án

Đáp án D

Câu 171:

Số nghiệm nguyên của bất phương trình $2 \log_{5} x - \log_{x} 125 < 1$ là

A. 1

B. 9

C. 10

D. 11

Xem đáp án

Đáp án C

Câu 172:

Số nghiệm nguyên của bất phương trình $\log_{3} x + \log_{3 x} 27 \leq 3$ là

A. 9

B. 0

C. 5

D. 11

Xem đáp án

Đáp án A

Câu 173:

Giải bất phương trình

\frac{\ln x + 2}{\ln x - 1} < 0

ta được tập nghiệm là

A.

(\frac{1}{e^{2}}; e)

B.

(- \infty; e)

C.

(- \infty; \frac{1}{e^{2}})

D.

(e; + \infty)

Xem đáp án

Đáp án A

Câu 174:

Mệnh đề nào sau đây đúng khi phát biểu về bất phương trình $\frac{3}{4 - 2 \log_{2} x} + \frac{1}{2 - 3 \log_{3} x} < 1$

A. Tập xác định của bất phương trình đã cho là $T = (0; + \infty)$

B. Tập xác định của bất phương trình đã cho là

T = [0; + \infty)

C. Tập xác định của bất phương trình đã cho là

T = (0; \frac{8}{27}) \cup (\frac{8}{27}; 4) \cup (4; + \infty)

D. Tập xác định của bất phương trình đã cho là

T = (0; \sqrt[3]{9}) \cup (\sqrt[3]{9}; 4) \cup (4; + \infty)

Xem đáp án

Đáp án D

Câu 175:

Tập nghiệm của bất phương trình $\frac{1}{2 - \ln x} + \frac{1}{\ln x} > 2$ là

A. $(- \infty; 0) \cup (1; e) \cup (e^{2}; + \infty)$

B.

(- \infty; 1)

C.

(1; e^{2}) \ \{e\}

D.

(- \infty; e) \cup (e^{2}; + \infty)

Xem đáp án

Đáp án C

Câu 176:

Tập nghiệm của bất phương trình $\frac{1}{\log_{6} e} > \frac{1}{\log_{4 - x} e} + \frac{1}{\log_{3 + x} e}$ là

A. $(- 3; - 2) \cup (3; 4)$

B.

(- 3; 4) \cup (- 3; 2)

C.

(- \infty; - 2) \cup (3; + \infty)

D.

(- \infty; - 3) \cup (4; + \infty)

Xem đáp án

Đáp án A

Câu 177:

Tập nghiệm của bất phương trình $\frac{1}{4 + \log_{2} x} + \frac{2}{2 - \log_{2} x} \leq 1$ là

A. $(0; \frac{1}{16}) \cup [\frac{1}{4}; \frac{1}{2}] \cup (2; 4) \cup (4; + \infty)$

B.

(0; \frac{1}{16}) \cup (\frac{1}{4}; \frac{1}{2}) \cup (2; 4) \cup (4; + \infty)

C.

(0; \frac{1}{16}) \cup [\frac{1}{4}; \frac{1}{2}] \cup [2; 4] \cup (4; + \infty)

D.

(0; \frac{1}{16}) \cup [\frac{1}{4}; \frac{1}{2}] \cup (4; + \infty)

Xem đáp án

Đáp án D

Câu 178:

Tập nghiệm của bất phương trình $\frac{16 \log_{2} x}{\log_{2} x^{2} + 3} - \frac{3 \log_{2} x^{2}}{\log_{2} x + 1} < 0$ là

A. $(0; 1) \cup (\sqrt{2}; + \infty)$

B.

(\frac{1}{2 \sqrt{2}}; \frac{1}{2}) \cup (1; + \infty)

C.

(\frac{1}{2 \sqrt{2}}; \frac{1}{2}) \cup (1; + \sqrt{2})

D.

(\frac{1}{2 \sqrt{2}}; 1) \cup (\sqrt{2}; + \infty)

Xem đáp án

Đáp án C

Câu 179:

Tìm m để bất phương trình $\log^{2} x - m \log x + m + 3 \leq 0$ có nghiệm $x > 1$

A.

[\begin{array}{l} m < - 3 \\ m \geq 6 \end{array}

B.

- 3 < m \leq 6

C.

m < - 3

D.

m \geq 6

Xem đáp án

Đáp án A

Câu 180:

Tập nghiệm của bất phương trình

\log_{x} [\log_{9} (3^{x} - 9)] < 1

là

A.

\emptyset

B. R

C.

(3; + \infty)

D.

(\log_{3} 10; + \infty)

Xem đáp án

Đáp án D

Câu 181:

Tập nghiệm của bất phương trình $\log_{x} [\log_{4} (2^{x} - 4)] \leq 1$ là

A. R

B.

\emptyset

C.

(\log_{2} 5; + \infty)

D.

(2; + \infty)

Xem đáp án

Đáp án C

Câu 182:

Số nghiệm nguyên của bất phương trình $\log_{2 x} (x^{2} - 5 x + 6) < 1$ là

A. 0

B. 1

C. 2

D. 3

Xem đáp án

Đáp án C

Câu 183:

Tập nghiệm của bất phương trình $\log_{\frac{x}{5}} (x^{2} - 8 x + 16) \geq 0$ là

A.

[3; + \infty) \ \{4\}

B.

[3; + \infty)

C.

(5; + \infty)

D.

[3; + \infty) \ \{5\}

Xem đáp án

Đáp án D

Câu 184:

Bất phương trình $\log_{2} (2^{x} + 1) + \log_{3} (4^{x} + 2) \leq 2$ có tập nghiệm

A.

(- \infty; 0)

B.

[0; + \infty)

C.

(- \infty; 0]

D.

(0; + \infty)

Xem đáp án

Đáp án C

Câu 185:

Giải bất phương trình $\log_{x} (\log_{3} (9^{x} - 72)) \leq 1$ ta được:

A.

x \leq 2

B.

\{\begin{cases} 0 < x \leq 2 \\ x \neq 1 \end{cases}

C.

\log_{9} 72 \leq x \leq 2

D.

\log_{9} 73 \leq x \leq 2

Xem đáp án

Đáp án D

Câu 186:

Tập nghiệm của bất phương trình

\log_{2} ({7.10}^{x} - {5.25}^{x}) > 2 x + 1

là

A.

[- 1; 0)

B.

(- 1; 0)

C.

[- 1; 0)

D.

[- 1; 0]

Xem đáp án

Đáp án B

Câu 187:

Bất phương trình

2 \log_{9} (9^{x} + 9) + \log_{\frac{1}{3}} (28 - {2.3}^{x}) \geq x

có tập nghiệm là

A. $(- \infty; - 1] \cup [2; \log_{3} 14]$

B.

(- \infty; - 1] \cup [2; \log_{3} 14)

C.

(- \infty; - 1] \cup [2; \frac{12}{5}]

D.

(- \infty; \log_{3} 14]

Xem đáp án

Đáp án B

Câu 188:

Với giá trị nào của tham số m thì bất phương trình $\log_{m} (x^{2} - 2 x + m + 5) > 1$ có vô số nghiệm

A.

m > 1

B.

0 < m < 1

C.

m \geq 1

D.

m > 0

Xem đáp án

Đáp án A