Đề thi cuối kì 1 Toán 12 Kết nối tri thức có đáp án - Đề 06
-
254 lượt thi
-
22 câu hỏi
-
90 phút
Danh sách câu hỏi
Câu 1:
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12.
Mỗi câu hỏi thí sinh chỉ chọn một phương án.
Cho hàm số ![]() xác định, liên tục trên đoạn
xác định, liên tục trên đoạn ![]() và có đồ thị là đường cong trong hình vẽ sau:
và có đồ thị là đường cong trong hình vẽ sau:
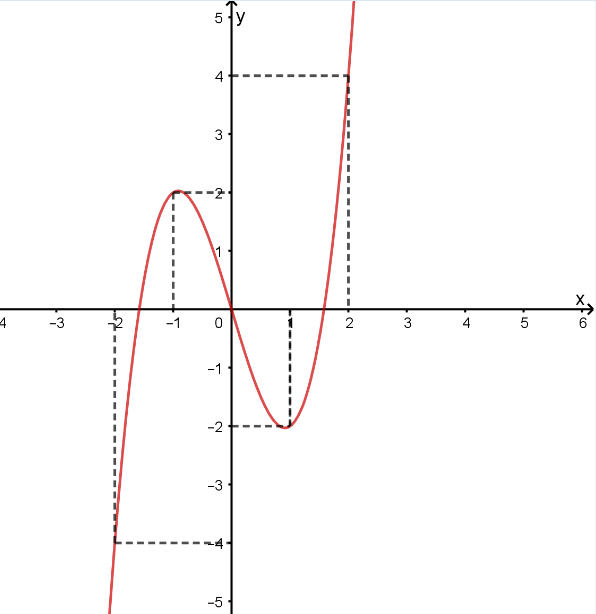
Tìm khẳng định đúng trong các khẳng định sau:
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
Quan sát đồ thị trên đoạn ![]() , giá trị nhỏ nhất của hàm số
, giá trị nhỏ nhất của hàm số ![]() là
là ![]() .
.
Câu 2:
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Tập xác định: ![]() .
.
Ta có ![]() .
.
Suy ra tiệm cận đứng của đồ thị hàm số là đường thẳng ![]() .
.
Câu 3:
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
Tập xác định ![]() .
.
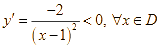 .
.Ta có ![]()
![]()
Vậy ![]() .
.
Câu 4:
Đường cong trong hình bên là đồ thị của hàm số
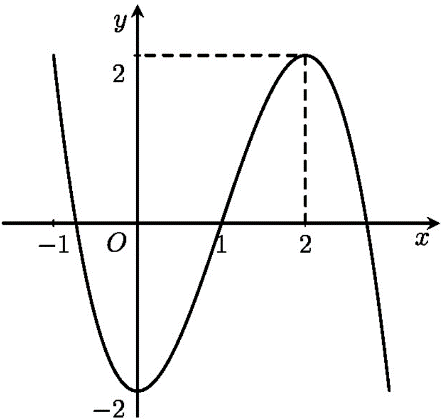
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Từ hình vẽ cho ta thấy đồ thị là hình dạng của đồ thị hàm số bậc ba ![]() có
có 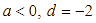 . Do đó, chọn câu C.
. Do đó, chọn câu C.
Câu 5:
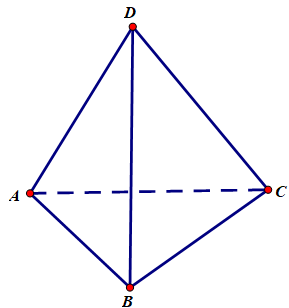
Cho tứ diện ![]() .Các véc tơ có điểm đầu là
.Các véc tơ có điểm đầu là ![]() và điểm cuối là các đỉnh còn lại của hình tứ diện là
và điểm cuối là các đỉnh còn lại của hình tứ diện là
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
Đó là các véc tơ: ![]()
Câu 7:
 Xem đáp án
Xem đáp án
Đáp án đúng là: C
Ta có ![]() .
.
Câu 9:
 Xem đáp án
Xem đáp án
Đáp án đúng là: D
Gọi ![]() .
.
Khi đó ![]()
![]() .
.
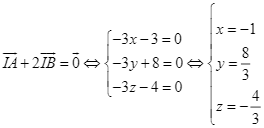 . Vậy
. Vậy ![]() .
.
Câu 11:
Cho mẫu số liệu ghép nhóm:
|
Nhóm |
|
|
|
|
|
|
Tần số |
|
|
|
|
|
trong đó các tần số 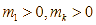 và
và ![]() là cỡ mẫu. Khoảng biến thiên của mẫu số liệu ghép nhóm trên là
là cỡ mẫu. Khoảng biến thiên của mẫu số liệu ghép nhóm trên là
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
Khoảng biến thiên của mẫu số liệu ghép nhóm trên là ![]() .
.
Câu 12:
 Xem đáp án
Xem đáp án
Đáp án đúng là: A
Ý nghĩa độ lệch chuẩn của mẫu số liệu ghép nhóm: Độ lệch chuẩn của mẫu số liệu ghép nhóm xấp xỉ cho độ lệch chuẩn của mẫu số liệu gốc. Độ lệch chuẩn được dùng để đo mức độ phân tán của mẫu số liệu ghép nhóm xung quanh số trung bình của mẫu số liệu đó. Độ lệch chuẩn càng lớn thì mẫu số liệu càng phân tán.
Câu 13:
PHẦN II. Câu trắc nghiệm đúng sai. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai.
Cho hàm số ![]() có đồ thị hàm số như hình bên dưới
có đồ thị hàm số như hình bên dưới
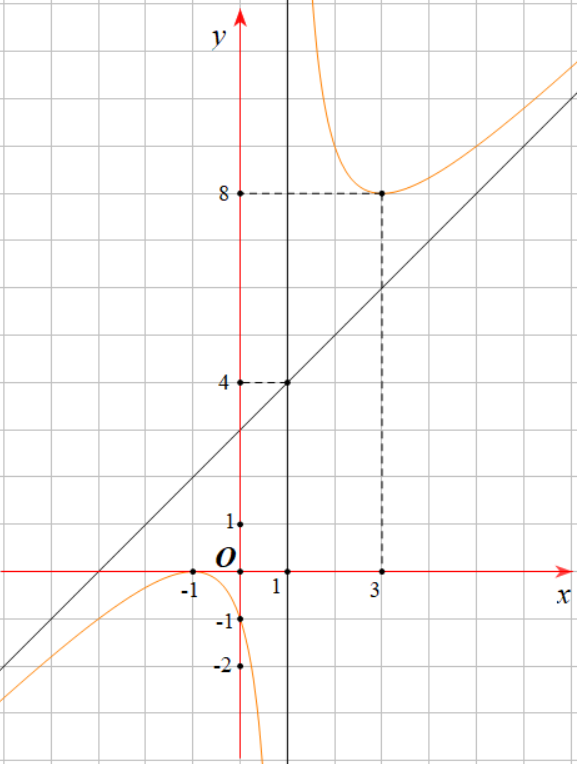
a) Hàm số ![]() đồng biến trên từng khoảng xác định
đồng biến trên từng khoảng xác định![]() và
và ![]() .
.
b) Hàm số ![]() đạt cực đại tại
đạt cực đại tại![]() và đạt cực tiểu tại
và đạt cực tiểu tại ![]() .
.
c) Đồ thị hàm số![]() ở hình trên là của hàm số
ở hình trên là của hàm số ![]() .
.
d) Điểm M trên đồ thị hàm số ![]() có khoảng cách đến I là nhỏ nhất (với I là giao điểm của hai tiệm cận) với hoành độ dương là
có khoảng cách đến I là nhỏ nhất (với I là giao điểm của hai tiệm cận) với hoành độ dương là![]() .
.
 Xem đáp án
Xem đáp án
a) S, b) Đ, c) Đ, d) Đ
a) Hàm số ![]() đồng biến trên từng khoảng
đồng biến trên từng khoảng ![]() và
và ![]() .
.
b) Điểm cực đại của đồ thị hàm số ![]() là
là ![]() và điểm cực tiểu của đồ thị hàm số
và điểm cực tiểu của đồ thị hàm số ![]() là
là ![]() .
.
c) Dựa vào đồ thị hàm số ta thấy ![]() là tiệm cận đứng của đồ thị hàm số,
là tiệm cận đứng của đồ thị hàm số, ![]() là tiệm cận xiên của đồ thị hàm số.
là tiệm cận xiên của đồ thị hàm số.
Đồ thị hàm số đi qua các điểm ![]() .
.
Ta thấy hàm số ![]() có
có ![]() là tiệm cận đứng của đồ thị hàm số,
là tiệm cận đứng của đồ thị hàm số, ![]() là tiệm cận xiên của đồ thị hàm số và đồ thị hàm số đi qua các điểm
là tiệm cận xiên của đồ thị hàm số và đồ thị hàm số đi qua các điểm 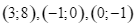
Câu 14:
Cho hàm số ![]() .
.
a) Hàm số đồng biến trên khoảng ![]() .
.
b) Hàm số đạt cực tiểu tại ![]() .
.
c) Giá trị lớn nhất của hàm số trên đoạn ![]() bằng
bằng ![]() .
.
d) Giá trị nhỏ nhất của hàm số ![]() trên đoạn
trên đoạn ![]() bằng
bằng ![]() .
.
 Xem đáp án
Xem đáp án
a) S, b) Đ, c) S, d) Đ
Ta có ![]() có
có ![]()
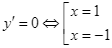
Bảng biến thiên
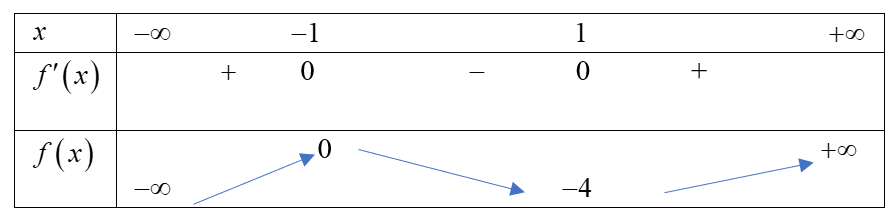
Dựa vào bảng biến thiên, ta có:
a) Hàm số nghịch biến trên khoảng ![]() .
.
b) Hàm số đạt cực tiểu tại ![]() .
.
c) Giá trị lớn nhất của hàm số trên đoạn ![]() bằng
bằng ![]() .
.
d) Ta có ![]()
Đặt ![]() ,
, ![]()
Theo câu a có giá trị nhỏ nhất của hàm số trên đoạn ![]() bằng
bằng ![]() .
.
Câu 15:
Trong không gian với hệ trục tọa độ ![]() , cho
, cho ![]() với
với ![]() là hai vectơ đơn vị trên hai trục tọa độ
là hai vectơ đơn vị trên hai trục tọa độ ![]() , hai điểm
, hai điểm ![]() .
.
a) ![]() .
.
b) Ba điểm ![]() thẳng hàng.
thẳng hàng.
c) Điểm ![]() là điểm đối xứng với
là điểm đối xứng với ![]() qua
qua ![]() . Khi đó
. Khi đó ![]() .
.
d) Điểm ![]() trên mặt phẳng
trên mặt phẳng ![]() sao cho
sao cho ![]() đạt giá trị nhỏ nhất. Khi đó
đạt giá trị nhỏ nhất. Khi đó ![]() .
.
 Xem đáp án
Xem đáp án
a) Đ, b) S, c) Đ, d) Đ
a) Vì ![]() .
.
b) Ta có ![]() .
.
Do ![]() không cùng phương nên suy ra
không cùng phương nên suy ra ![]() không thẳng hàng.
không thẳng hàng.
c) Điểm ![]() là điểm đối xứng với
là điểm đối xứng với ![]() qua
qua ![]() nên
nên ![]() là trung điểm của
là trung điểm của ![]() .
.
Ta có 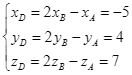 . Suy ra
. Suy ra ![]() .
.
Suy ra ![]() . Vậy
. Vậy ![]() .
.
d) Gọi ![]() là điểm thỏa mãn
là điểm thỏa mãn ![]() .
.
Ta có 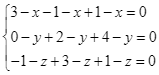
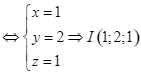 .
.
Ta có ![]()
![]()
![]()
![]() .
.
Do ![]() không thay đổi nên
không thay đổi nên ![]() nhỏ nhất khi
nhỏ nhất khi ![]() nhỏ nhất hay
nhỏ nhất hay ![]() là hình chiếu của điểm
là hình chiếu của điểm ![]() trên mặt phẳng
trên mặt phẳng ![]() .
.
Do đó ![]() . Suy ra
. Suy ra ![]() . Vậy
. Vậy ![]() .
.
Câu 16:
Thống kê chiều cao của tổ 1 và tổ 2 của lớp 10A cho bởi bảng sau:
|
Chiều cao (cm) |
|
|
|
|
|
|
|
Số học sinh tổ 1 |
3 |
2 |
2 |
1 |
3 |
0 |
|
Số học sinh tổ 2 |
1 |
3 |
3 |
2 |
1 |
1 |
a) Tứ phân vị thứ nhất của mẫu số liệu về chiều cao của học sinh tổ 1 là ![]() .
.
b) Khoảng biến thiên của mẫu số liệu về chiều cao của học sinh tổ 1 là ![]() .
.
c) Phương sai của mẫu số liệu về chiều cao của học sinh tổ 2 là ![]() .
.
d) Độ lệch chuẩn của mẫu số liệu về chiều cao của học sinh tổ 2 lớn hơn độ lệch chuẩn của mẫu số liệu về chiều cao của học sinh tổ 1.
 Xem đáp án
Xem đáp án
a) S, b) Đ, c) Đ, d) S
a) Xét mẫu số liệu về chiều cao của học sinh tổ 1:
Cỡ mẫu ![]() .
.
Tứ phân vị thứ nhất của mẫu số liệu là ![]() nên nhóm chứa tứ phân vị thứ nhất là
nên nhóm chứa tứ phân vị thứ nhất là ![]() và ta có
và ta có 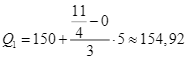 .
.
b) Khoảng biến thiên của mẫu số liệu về chiều cao của học sinh tổ 1 là ![]() .
.
c) Xét mẫu số liệu về chiều cao của học sinh tổ 2:
![]() .
.
![]() .
.
d) Độ lệch chuẩn của mẫu số liệu về chiều cao của học sinh tổ 2 là ![]() .
.
Xét mẫu số liệu về chiều cao của học sinh tổ 1:
![]() .
.
![]() .
.
![]() . Ta thấy
. Ta thấy ![]() .
.
Câu 17:
 Xem đáp án
Xem đáp án
Trả lời: 1
Từ giả thiết, ta có bảng biến thiên của hàm số ![]()
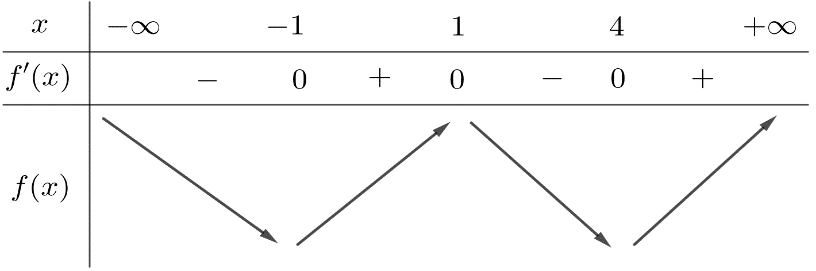
Ta có ![]()
![]()
![]() .
.
Từ bảng biến thiên của hàm số![]() ta có
ta có
![]()
![]()
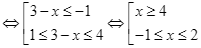 .
.
Như thế ta có bảng biến thiên của hàm số ![]()
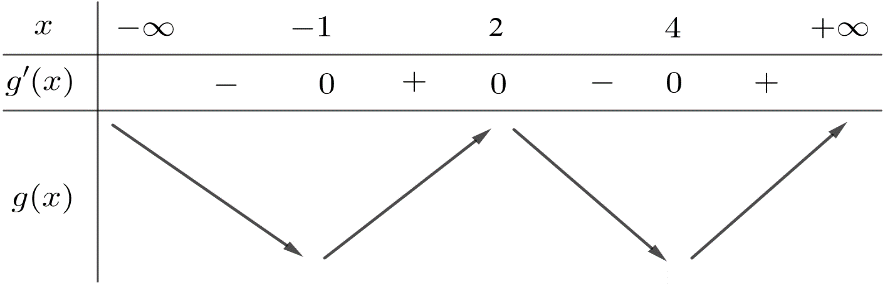
Từ bảng biến thiên, ta nhận thấy hàm số ![]() có 1 điểm cực đại.
có 1 điểm cực đại.
Câu 18:
 Xem đáp án
Xem đáp án
Trả lời: 52
Xét hàm số:
![]() .
.
![]() .
.
TXĐ: ![]() .
.
Ta có 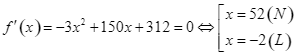 .
.
Bảng biến thiên:

Hàm số đạt giá trị cực đại ![]() tại
tại ![]() .
.
Câu 19:
 Xem đáp án
Xem đáp án
Trả lời: 8
Ta có 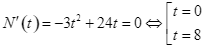 .
.
Bảng biến thiên
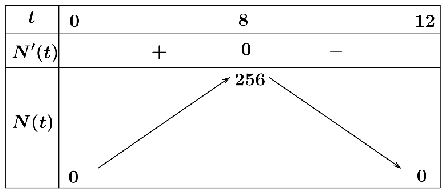
Từ bảng biến thiên ta thấy số người bị nhiễm bệnh tăng trong khoảng thời gian ![]() .
.
Suy ra ![]() . Vậy
. Vậy ![]() .
.
Câu 20:
 Xem đáp án
Xem đáp án
Trả lời: 1
![]() là trọng tâm tam giác
là trọng tâm tam giác ![]() , suy ra
, suy ra ![]() .
.
Gọi ![]() là hình chiếu vuông góc của
là hình chiếu vuông góc của ![]() trên mặt phẳng
trên mặt phẳng ![]() . Khi đó
. Khi đó ![]() là khoảng cách từ
là khoảng cách từ ![]() đến mặt phẳng
đến mặt phẳng ![]() , ta có
, ta có ![]() .
.
Với ![]() là điểm thay đổi trên mặt phẳng
là điểm thay đổi trên mặt phẳng ![]() , ta có
, ta có ![]() .
.
Do đó ![]() ngắn nhất
ngắn nhất ![]() . Vậy độ dài
. Vậy độ dài ![]() ngắn nhất bằng 1.
ngắn nhất bằng 1.
Câu 21:
Những căn lều gỗ trong Hình 1 được phác thảo dưới dạng một hình lăng trụ đứng tam giác ![]() như trong Hình 2. Với hệ trục toạ độ
như trong Hình 2. Với hệ trục toạ độ ![]() thể hiện như Hình 2 (đơn vị đo lấy theo centimét), hai điểm
thể hiện như Hình 2 (đơn vị đo lấy theo centimét), hai điểm ![]() và
và ![]() có tọa độ lần lượt là
có tọa độ lần lượt là ![]() và
và ![]() . Mỗi căn nhà gỗ có chiều dài là
. Mỗi căn nhà gỗ có chiều dài là ![]() , chiều rộng là
, chiều rộng là ![]() , mỗi cạnh bên của mặt tiền có độ dài là
, mỗi cạnh bên của mặt tiền có độ dài là ![]() . Tính
. Tính ![]() (Làm tròn đến hàng đơn vị).
(Làm tròn đến hàng đơn vị).
|
|
|
|
Hình 1 |
Hình 2 |
 Xem đáp án
Xem đáp án
Trả lời: 1013
Vì điểm ![]() có toạ độ là
có toạ độ là ![]() nên khoảng cách từ
nên khoảng cách từ ![]() đến các trục
đến các trục ![]() lần lượt là
lần lượt là ![]() và
và ![]() . Suy ra
. Suy ra ![]() và
và ![]() .
.
Từ giả thiết suy ra ![]() ,
,
do đó ![]() .
.
Vì ![]() và
và ![]() nằm trên trục
nằm trên trục ![]() nên toạ độ của điểm
nên toạ độ của điểm ![]() là
là ![]() .
.
Do đó ![]() và
và ![]() .
.
Vậy mỗi căn lều gỗ có chiều dài là ![]() , chiều rộng là
, chiều rộng là ![]() , mỗi cạnh bên của mặt tiền có độ dài là 323 cm.
, mỗi cạnh bên của mặt tiền có độ dài là 323 cm.
![]() .
.
Câu 22:
Một trang báo điện tử thống kê thời gian người sử dụng đọc thông tin trên trang trong mỗi lần truy cập ở bảng sau:
|
Thời gian đọc (phút) |
[0; 2) |
[2; 4) |
[4; 6) |
[6; 8) |
[8; 10) |
|
Số lượt truy cập |
45 |
34 |
23 |
18 |
5 |
Hãy tìm khoảng tứ phân vị của mẫu số liệu ghép nhóm trên (kết quả làm tròn đến hàng phần trăm).
 Xem đáp án
Xem đáp án
Trả lời: 3,89
Cỡ mẫu là ![]() .
.
Gọi ![]() là thời gian đọc thông tin trên trang báo điện tử của 125 lượt truy cập và giả sử rằng dãy số liệu gốc này đã được sắp xếp theo thứ tự tăng dần.
là thời gian đọc thông tin trên trang báo điện tử của 125 lượt truy cập và giả sử rằng dãy số liệu gốc này đã được sắp xếp theo thứ tự tăng dần.
Tứ phân vị thứ nhất của mẫu số liệu gốc là ![]() nên nhóm chứa tứ phân vị thứ nhất là nhóm [0; 2) và ta có:
nên nhóm chứa tứ phân vị thứ nhất là nhóm [0; 2) và ta có:
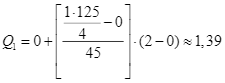 .
.
Tứ phân vị thứ ba của mẫu số liệu gốc là ![]() nên nhóm chứa tứ phân vị thứ nhất là nhóm [4; 6) và ta có:
nên nhóm chứa tứ phân vị thứ nhất là nhóm [4; 6) và ta có:
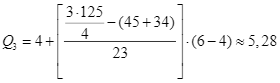 .
.
Vậy khoảng tứ phân vị của mẫu số liệu ghép nhóm là: ![]() .
.