10 câu hỏi trắc nghiệm thuộc Đề kiểm tra 15 phút Toán 12 Chương 3 Hình học có đáp án (Đề 3)

Top 8 Đề kiểm tra Toán 12 Chương 3 Hình học có đáp án

Đề kiểm tra 15 phút Toán 12 Chương 3 Hình học có đáp án (Đề 3)

4116 lượt thi
10 câu hỏi
15 phút

Danh sách câu hỏi

Câu 1:

Trong không gian Oxyz, viết phương trình mặt phẳng (P) đi qua điểm $A (1; 0; - 2)$ và có vectơ pháp tuyến $\vec{n} (1; - 1; 2)$ .

A. x - y + 2z – 3 = 0

B. x - y + 2z + 3 = 0

C. x - 2z + 3 = 0

D. x + 2z – 3 = 0

Xem đáp án

Chọn B.

Mặt phẳng (P) đi qua điểm A(1;0;-2) và có vectơ pháp tuyến 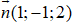có phương trình là:

1(x - 1) - 1(y - 0) + 2(z + 2) = 0 ⇔ x - y + 2z + 3 = 0.

Vậy phương trình mặt phẳng (P) là: x- y + 2z + 3 = 0.

Câu 2:

Trong không gian Oxyz, cho hai mặt phẳng $(P) : 2 x - m y - 4 z - 6 + m = 0 v à (Q) : (m + 3) x + y + (5 m + 1) z - 7 = 0 .$ Tìm m để hai mặt phẳng (P) và (Q) trùng nhau

A. $m = - \frac{6}{5}$

B. m = 1

C. m = -1

D. m = 4

Xem đáp án

Chọn C.

Để hai mặt phẳng (P) và (Q) trùng nhau khi và chỉ khi:

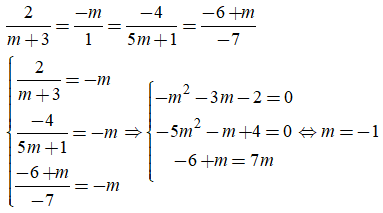
Câu 3:

Trong không gian Oxyz, cho hai mặt phẳng $(P) : 2 x + m y + 2 m z - 9 = 0 v à (Q) : 6 x - y - z - 10 = 0 . T ì m$ m để (P) ⊥ (Q).

A. m = 4

B. m = -4

C. m = -2

D. m = 2

Xem đáp án

Chọn A.

Để hai mặt phẳng (P) và (Q) vuông góc với nhau khi:

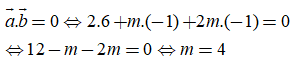
Câu 4:

Trong không gian Oxyz, viết phương trình mặt phẳng (P) đi qua điểm M(0;1;3) và song song với mặt phẳng $(Q) : 2 x - 3 z + 1 = 0 .$

A. 2x - 3z - 10 = 0

B. 2x + 3z – 9 = 0

C. 2x - 3z + 9 = 0

D. 2x + 3z + 1 = 0

Xem đáp án

Chọn C.

Mặt phẳng (P) song song với mặt phẳng (Q):2x - 3z + 1 = 0 nên mặt phẳng (P) có phương trình dạng: 2x - 3z + D = 0 (D ≠ 1).

Mặt phẳng (P) đi qua điểm M nên thay tọa độ điểm vào phương trình mặt phẳng (P) ta được:

2.0 - 3.3 + D = 0 ⇔ D = 9 (thỏa mãn D ≠ 1).

Vậy phương trình mặt phẳng (P) là: 2x - 3z + 9 = 0.

Câu 5:

Trong không gian Oxyz, viết phương trình mặt phẳng đi qua ba điểm $A (1; 0; - 2), B (1; 1; 1), C (0; - 1; 2) .$

A. 7x - 3y + z – 1 = 0

B. 7x + 3y + z + 3 = 0

C. 7x + 3y + z + 1 = 0

D. 7x – 3y + z – 5 = 0

Xem đáp án

Chọn D.

Ta có: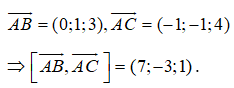

Gọi $\vec{n}$ là một vectơ pháp tuyến của mặt phẳng (ABC) ta có

ta được phương trình mặt phẳng (ABC) là:

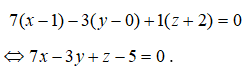
Câu 6:

Trong không gian Oxyz, viết phương trình mặt phẳng (α) đi qua điểm $A (1; 2; - 2), B (2; - 1; 4)$ và vuông góc với $(β) : x - 2 y - z + 1 = 0 .$

A. 15x + 7y + z – 27 = 0

B. 15x – 7y + z + 1 = 0

C. 15x – 7y – z + 1 = 0

D. Đáp án khác

Xem đáp án

Chọn A.

Mặt phẳng chứa A, B và vuông góc với (β) nên (α) có một vectơ pháp tuyến là:

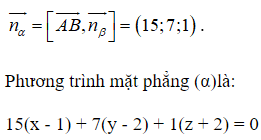
Câu 7:

Trong không gian Oxyz, viết phương trình mặt phẳng (P) đi qua điểm $M (- 1; - 2; 5)$ và vuông góc với hai mặt phẳng $(Q) : x + 2 y - 3 z + 1 = 0 v à (R) : 2 x - 3 y + z + 1 = 0 .$

A. x- y + z – 6 = 0

B. x + y - z + 8 = 0

C. –x + y + z – 4 = 0

D. x + y + z - 2 = 0

Xem đáp án

Chọn D

nên mặt phẳng (P) nhận

và (P) đi qua điểm M(-1;-2;5) nên có phương trình là:

$1 (x + 1) + 1 (y + 2) + 1 (z - 5) = 0 h a y x + y + z - 2 = 0 .$

Câu 8:

Trong không gian Oxyz, viết phương trình mặt phẳng (P) song song với mặt phẳng $(Q) : x + 2 y - 2 z + 1 = 0$ và cách (Q) một khoảng bằng 3.

A. $x + 2 y - 2 z + 8 = 0 v à x + 2 y - 2 z - 10 = 0 .$

B. $x + 2 y - 2 z + 6 = 0 v à x + 2 y - 2 z - 8 = 0$

C. $x + 2 y - 2 z - 8 = 0 v à x + 2 y - 2 z + 10 = 0$

D. Đáp án khác.

Xem đáp án

Chọn C.

Trên mặt phẳng (Q): x + 2y - 2z + 1 = 0 chọn điểm M (-1;0;0).

Do (P) song song với mặt phẳng (Q) nên phương trình của mặt phẳng (P) có dạng: x + 2y - 2z + D = 0 với D ≠ 1.

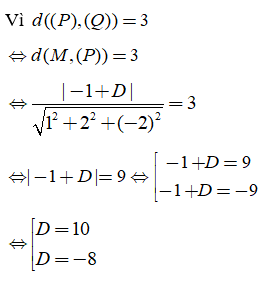
Vậy có hai mặt phẳng thỏa mãn: x + 2y – 2z + 10 = 0 và x + 2y -2z – 8 = 0.

Câu 9:

Trong không gian Oxyz, viết phương trình mặt phẳng (P) song song với mặt phẳng $(Q) : x + 2 y - 2 z + 1 = 0$ và tiếp xúc với mặt cầu $(S) : x^{2} + y^{2} + z^{2} + 2 x - 4 y - 2 z - 3 = 0$

A. $x + 2 y - 2 z + 12 = 0 v à x + 2 y - 2 z - 6 = 0$

B. $x + 2 y - 2 z - 12 = 0 v à x + 2 y - 2 z + 6 = 0$

C. $x + 2 y - 2 z + 10 = 0 v à x + 2 y - 2 z - 8 = 0$

D. $x + 2 y - 2 z - 10 = 0 v à x + 2 y - 2 z + 8 = 0$

Xem đáp án

Chọn D.

Mặt cầu (S) có tâm I(-1;2;1) và bán kính

Do (P) song song với mặt phẳng (Q) nên phương trình của mặt phẳng (P) có dạng:

x + 2y – 2z + D = 0 với D ≠ 1.

Vì (P) tiếp xúc với mặt cầu (S) nên d(I;(P)) = R = 3

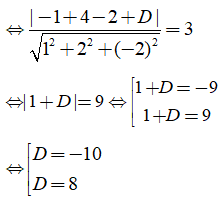
Vậy có hai mặt phẳng thỏa mãn: x + 2y – 2z – 10 = 0 và x + 2y – 2z + 8 = 0

Câu 10:

Trong không gian với hệ trục tọa độ Oxyz, cho hai mặt phẳng $(α) : 3 x + (m - 1) y + 4 z - 2 = 0, (β) : n x + (m + 2) y + 2 z + 4 = 0 .$ Với giá trị thực của m, n bằng bao nhiêu để (α) song song (β)

A. $m = - 5; n = \frac{3}{2}$

B. $m = - 5; n = \frac{5}{2}$

C. $m = - 3; n = \frac{3}{2}$

D. $m = - 3; n = \frac{5}{2}$

Xem đáp án

Chọn A.

Để (α) song song (β)

Bắt đầu thi ngay