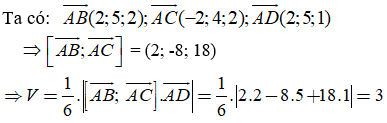Đề kiểm tra 45 phút Toán 12 Chương 3 Hình học có đáp án (Đề 2)
-
4242 lượt thi
-
25 câu hỏi
-
45 phút
Danh sách câu hỏi
Câu 1:
Trong không gian tọa độ Oxyz, cho ba điểm Để tứ giác ABCD là hình bình hành thì tọa độ điểm D là
 Xem đáp án
Xem đáp án
Chọn A
Điểm D(x;y;z)
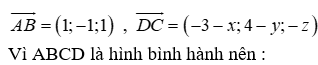
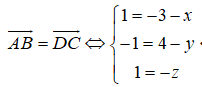
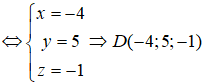
Câu 2:
Cho điểm điểm đối xứng của M qua mặt phẳng (Oxy) là điểm
 Xem đáp án
Xem đáp án
Chọn C.
Với M(x, y, z) thì điểm đối xứng của M qua mặt phẳng (Oxy) là N(x,y,-z)
Do đó, điểm đối xứng với M(3;2;-1) qua mặt phẳng (Oxy) là điểm N(3;2;1).
Câu 4:
Trong không gian Oxyz, cho ba điểm Giá trị của x, y để ba điểm A; B; C thẳng hàng là
 Xem đáp án
Xem đáp án
Chọn A.
![]()
Để 3 điểm A, B, C thẳng hàng khi và chi khi cùng phương
![]()
Câu 5:
Mặt cầu có tọa độ tâm và bán kính R là:
 Xem đáp án
Xem đáp án
Chọn A.
Phương trình mặt cầu (S) có dạng x2 + y2 + z2 - 2ax - 2by - 2cz + d = 0 với a2 + b2 + c2 - d > 0, có tâm I(a;b;c), bán kính![]()
Do đó, mặt cầu (S) có tâm I(2;0;0) và bán kính: ![]()
Câu 6:
Viết phương trình mặt cầu (S) có đường kính AB với
 Xem đáp án
Xem đáp án
Chọn C
Ta có:
![]()
Gọi I là trung điểm AB nên 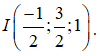
Mặt cầu tâm 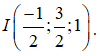 và bán kính
và bán kính 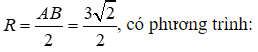
Câu 7:
Viết phương trình mặt cầu (S) có tâm I thuộc đường thẳng và (S) tiếp xúc với hai mặt phẳng
 Xem đáp án
Xem đáp án
Chọn A.
Gọi I(t;-1;-t) ∈ Δ là tâm mặt cầu (S) cần tìm.
Theo giả thiết mặt cầu tiếp xúc với hai mặt phẳng (P) và (Q) nên:
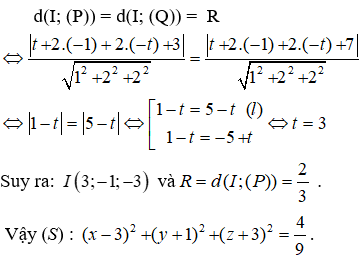
Câu 8:
Cho đường thẳng và điểm Đường thẳng d cắt mặt cầu (S) có tâm I, tại hai điểm A, B sao cho Phương trình của mặt cầu (S) là:
 Xem đáp án
Xem đáp án
Chọn A
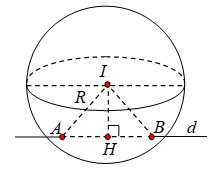
Đường thẳng d đi qua M(-5;7;0) và có vectơ chỉ phương ![]()
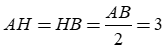
Gọi H là hình chiếu của I lên (d). Ta có:
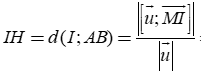
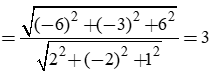
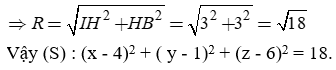
Câu 9:
Trong không gian với hệ toạ độ Oxyz, cho ba điểm A(1;-2;1); B(-1;3;3); C(2;-4;2). Một vectơ pháp tuyến 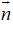
 Xem đáp án
Xem đáp án
Chọn A
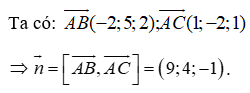
Câu 10:
Trong không gian Oxyz, viết phương trình mặt phẳng (P) đi qua điểm và song song với mặt phẳng
 Xem đáp án
Xem đáp án
Chọn B
Mặt phẳng (P) song song với mặt phẳng (Q): 2x – 3z + 1 = 0 nên mặt phẳng (P) có phương trình dạng: 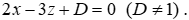
Mặt phẳng (P) đi qua điểm M(0;1;3) nên thay tọa độ điểm vào phương trình mặt phẳng (P) Ta được: 2.0 -3.3 + D = 0 ⇔ D = 9 (thỏa mãn D ≠ 1).
Vậy phương trình mặt phẳng (P) là: 2x – 3z + 9 = 0.
Câu 11:
Trong không gian Oxyz, cho mặt phẳng và đường thẳng . Trong các mệnh đề sau, mệnh đề nào đúng?
 Xem đáp án
Xem đáp án
Chọn A.
Mặt phẳng (P): 3x – 3y + 2z - 5 = 0 có VTPT
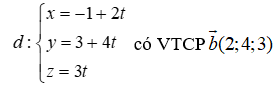
và đi qua A(-1;3;0)
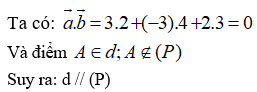
Câu 12:
Trong không gian Oxyz, viết phương trình mặt phẳng (P) chứa đường thẳng và song song với đường thẳng .
 Xem đáp án
Xem đáp án
Chọn D.
Đường thẳng d1 đi qua điểm M1(1;1;1) vectơ chỉ phương
Đường thẳng d2 đi qua điểm M2(1;0;1) vectơ chỉ phương
![]()
Gọi là một vectơ pháp tuyến của mặt phẳng (P), ta có:

Mặt phẳng (P) đi qua điểm M1(1;1;1) và nhận vectơ pháp tuyến có phương trình:
-6(x - 1) + 1(y - 1) + 2(z - 1) = 0 hay – 6x + y + 2z + 3 = 0.
Câu 13:
Cho đường thẳng và mặt phẳng Góc giữa đường thẳng ∆ và mặt phẳng (P) là:
 Xem đáp án
Xem đáp án
Chọn C.
Gọi lần lượt là vectơ chỉ phương, pháp tuyến của đường thẳng ∆ và mặt phẳng (P) ![]()
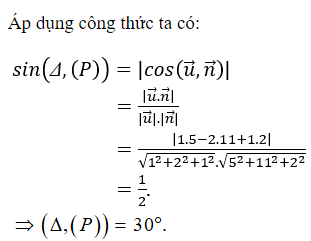
Câu 14:
Trong không gian Oxyz, cho đường thẳng và mặt cầu Số điểm chung của ∆ và (S) là:
 Xem đáp án
Xem đáp án
Chọn D.
Đường thẳng ∆ đi qua M (0;1;2) và có VTCP
Mặt cầu (S) có tâm I(1;0;-2) và bán kính R = 2
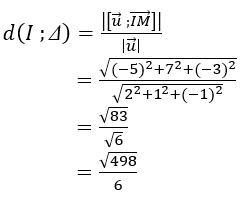
Vì d(I;Δ) > R nên ∆ không cắt mặt cầu (S)
Câu 15:
Trong không gian Oxyz, viết phương trình mặt phẳng (P) song song với mặt phẳng và tiếp xúc với mặt cầu
 Xem đáp án
Xem đáp án
Chọn C.
Trên mặt phẳng (Q): x + 2y - 2z + 1 = 0 chọn điểm M (-1;0;0).
Do (P) song song với mặt phẳng (Q) nên phương trình của mặt phẳng (P) có dạng: x + 2y - 2z + D = 0 với D ≠ 1.
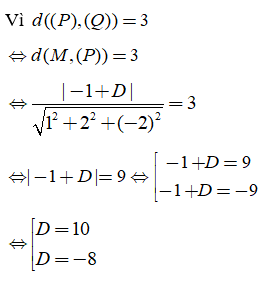
Vậy có hai mặt phẳng thỏa mãn: x + 2y – 2z + 10 = 0 và x + 2y -2z – 8 = 0.
Câu 16:
Trong không gian với hệ trục tọa độ Oxyz, cho hai mặt phẳng:
Với giá trị thực của m, n bằng bao nhiêu để (α) song song (β).
 Xem đáp án
Xem đáp án
Chọn C.
Để (α) song song (β) khi và chỉ khi:
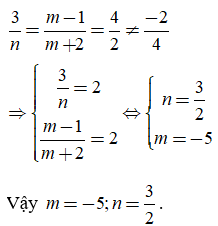
Câu 17:
Trong không gian với hệ toạ độ Oxyz, cho hai đường thẳng lần lượt có phương trình . Phương trình mặt phẳng (P) cách đều hai đường thẳng d1;d2 là:
 Xem đáp án
Xem đáp án
Chọn D.
Ta có d1 đi qua A(2;2;3) và có ![]()
![]()
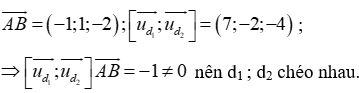
Do (P) cách đều d1;d2 nên (P) song song với
![]()
(P) có dạng 7x – 2y – 4z + d = 0
Vì (P) cách đều hai đường thẳng nên: d(A;(P)) = d(B;(P))
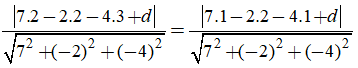
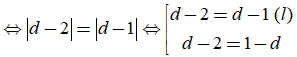
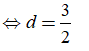
![]()
![]()
![]()
Câu 18:
Trong không gian với hệ tọa độ Oxyz, cho đường thẳng . Đường thẳng d đi qua điểm M và có vectơ chỉ phương có tọa độ là:
 Xem đáp án
Xem đáp án
Chọn C
Đường thẳng d đi qua điểm M(-2;1;3) và có vectơ chỉ phương .
Câu 19:
Trong không gian Oxyz, cho hai đường thẳng . Trong các mệnh đề sau, mệnh đề nào đúng khi nói về vị trí tương đối của hai đường thẳng trên?
 Xem đáp án
Xem đáp án
Chọn B.
Đường thẳng d có VTCP ![]()
Đường thẳng d’ có VTCP ![]()
Từ đó ta có:
![]()
Lại có:
![]()
Suy ra d và d’ chéo nhau.
Câu 20:
Trong không gian với hệ tọa độ Oxyz, phương trình nào sau đây là phương trình chính tắc ∆ của đường thẳng đi qua hai điểm A
 Xem đáp án
Xem đáp án
Chọn A.
∆ đi qua hai điểm A và B nên có vectơ chỉ phương
Vậy phương trình chính tắc của ∆ là
Câu 21:
Trong không gian với hệ tọa độ Oxyz, phương trình đường thẳng ∆ đi qua điểm và vuông góc với mặt phẳng (Oxz) là.
 Xem đáp án
Xem đáp án
Chọn C.
Mặt phẳng (Oxz) có vectơ pháp tuyến
Vì ∆ vuông góc với mp(Oxz) nên ∆ có vectơ chỉ phương 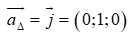
∆ đi qua điểm A(2;-1;3) và có vectơ chỉ phương
Vậy phương trình tham số của ∆ là
Câu 22:
Trong không gian với hệ tọa độ Oxyz, cho hai đường thẳng . Phương trình đường thẳng ∆ đi qua điểm và vuông góc với hai đường thẳng là
 Xem đáp án
Xem đáp án
Chọn B.
Đường thẳng d1 có vectơ chỉ phương ![]()
Đường thẳng d2 có vectơ chỉ phương ![]()
Vì ∆ vuông góc với d1;d2 nên 1 vecto chỉ phương của ∆ là: ![]()
Vậy phương trình tham số của ∆ là
Câu 23:
Trong không gian với hệ tọa độ Oxyz, cho đường thẳng và mặt phẳng . Phương trình tham số của đường thẳng d nằm trong (P), cắt và vuông góc đường thẳng ∆ là:
 Xem đáp án
Xem đáp án
Chọn D.
![]()
Vì M thuộc ∆ nên tọa độ M(-2+t;2 t;-t)
Mà điểm M thuộc mp (P) thay tọa độ điểm M vào phương trình mp(P) ta được:
-2 + t + 2(2 + t) - 3.(-t) + 4 = 0
⇔ 6t + 6 = 0 ⇔ t = -1 ⇒ M(-3;1;1)
Mặt phẳng (P) có vectơ pháp tuyến 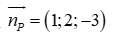
Đường thẳng ∆ có vectơ chỉ phương ![]()
Có
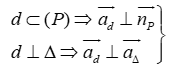
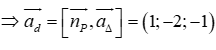
Đường thẳng d đi qua điểm M(-3;1;1) và có vectơ chỉ phương là .
Vậy phương trình tham số của d là
Câu 24:
Trong không gian với hệ tọa độ Oxyz, cho hai đường thẳng . Phương trình đường thẳng song song với và cắt hai đường thẳng ∆1;∆2 là:
 Xem đáp án
Xem đáp án
Chọn A.
Gọi ∆ là đường thẳng cần tìm
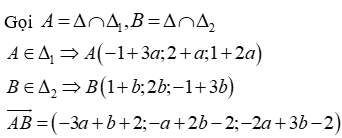
Đường thẳng d có vecto chỉ phương
![]()
![]()
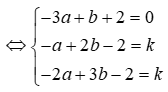
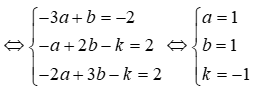
Ta có A(2;3;3); B(2;2;2)
∆ đi qua điểm A(2;3;3) và có vectơ chỉ phương ![]()
Vậy phương trình của ∆ là