8 câu hỏi trắc nghiệm thuộc Đề kiểm tra 15 phút Toán 12 Chương 3 Hình học có đáp án (Đề 5)

Top 8 Đề kiểm tra Toán 12 Chương 3 Hình học có đáp án

Đề kiểm tra 15 phút Toán 12 Chương 3 Hình học có đáp án (Đề 5)

4082 lượt thi
8 câu hỏi
15 phút

BẮT ĐẦU LÀM BÀI

Danh sách câu hỏi

Câu 1:

Mặt cầu $(S) : x^{2} + y^{2} + z^{2} - 4 x + 1 = 0$ có tọa độ tâm và bán kính R là:

A. I(2;0;0), $R = \sqrt{3}$

B. I(2;0;0), R=3

C. I(0;2;0), $R = \sqrt{3}$

D. I(-2;0;0), $R = \sqrt{3}$

Xem đáp án

Chọn A.

Phương trình mặt cầu (S) có dạng x2 + y2 + z2 - 2ax - 2by - 2cz + d = 0 với a2 + b2 + c2 - d > 0, có tâm I(a;b;c), bán kính

Do đó, mặt cầu (S) có tâm I(2;0;0) và bán kính:

Câu 2:

Phương trình mặt cầu có tâm $I (- 1; 2; - 3),$ bán kính R = 3 là:

A. ${(x - 1)}^{2} + {(y + 2)}^{2} + {(z - 3)}^{2} = 9$

B. ${(x + 1)}^{2} + {(y - 2)}^{2} + {(z + 3)}^{2} = 3$

C. ${(x + 1)}^{2} + {(y - 2)}^{2} + {(z + 3)}^{2} = 9$

D. ${(x + 1)}^{2} + {(y - 2)}^{2} + {(z + 3)}^{2} = 9$

Xem đáp án

Chọn C.

Mặt cầu có tâm I(-1;2;-3), bán kính R = 3 có phương trình:

(x + 1)2 + (y - 2)2 + (z + 3)2 = 9.

Câu 3:

Trong không gian Oxyz, cho mặt cầu $(S) : x^{2} + y^{2} + z^{2} - 2 x - 2 z - 7 = 0$ , mặt phẳng $(P) : 4 x + 3 y + m = 0$ . Giá trị của m để mặt phẳng (P) cắt mặt cầu (S).

A. m > 11 hoặc m < -19

B. -19 < m < 11

C. -12 < m < 4

D. m > 4 hoặc m < -12

Xem đáp án

Chọn B.

Mặt cầu có tâm I(1;0;1) và bán kính

Để (P) cắt mặt cầu (S)

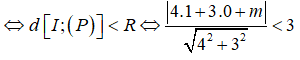
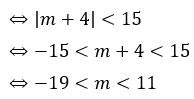
Câu 4:

Trong không gian Oxyz, cho mặt phẳng $(P) : 2 x + 3 y + z - 11 = 0 .$ Mặt cầu (S) có tâm I(1;-2;1) và tiếp xúc với mặt phẳng (P) tại đim H, khi đó H có tọa độ là:

A. H(-3;-1;-2)

B. H(-1;-5;0)

C. H(1;5;0)

D. H(3;1;2)

Xem đáp án

Chọn D.

*) Mặt cầu (S) có tâm I( 1; -2; 1) và tiếp xúc với mặt phẳng (P) tại điểm H nên H là hình chiếu của I lên (P).

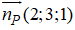
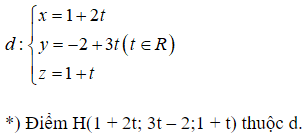
*) Lập phương trình đường thẳng d qua I và vuông góc với (P): d nhận làm vecto chỉ phương nên có phương trình:

$\Leftrightarrow t = 1$

=> H(3;1;2)

Câu 5:

Viết phương trình mặt cầu (S) biết (S) qua bốn điểm $A (1; 2; - 4); B (1; - 3; 1); C (2; 2; 3) v à D (1; 0; 4) .$

A. ${(x + 2)}^{2} + {(y - 1)}^{2} + z^{2} = 26$

B. ${(x - 2)}^{2} + {(y + 1)}^{2} + z^{2} = 13$

C. ${(x + 2)}^{2} + {(y + 1)}^{2} + z^{2} = 52$

D. Đáp án khác

Xem đáp án

Chọn A.

Gọi phương trình mặt cầu (S): x2 + y2 + z2 - 2ax - 2by - 2cz + d = 0, (a2 + b2 + c2 - d > 0)

có tâm I (a;b;c) và bán kính

Do A(1;2;-4) ∈ (S)nên: 12 + 22 + (-42 – 2.a.1 – 2b .2 - 2c.(-4) + d = 0 hay -2a - 4b + 8c + d = -21 (1)

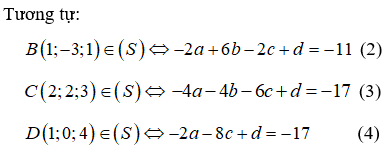
Giải hệ (1), (2), (3), (4) ta có: a = -2; b = 1; c = 0; d = -21, suy ra phương trình mặt cầu (S) :

(x + 2)2 + (y - 1)2 + z2 = 26.

Câu 6:

Cho đường thẳng $(∆) : \frac{x}{2} = \frac{y - 1}{1} = \frac{z - 2}{- 1}$ và và mặt cầu $(S) : x^{2} + y^{2} + z^{2} - 2 x + 4 z + 1 = 0 .$ Số điểm chung của (Δ) và (S) là :

A. 0

B. 1

C. 2

D. 3

Xem đáp án

Chọn A.

Đường thẳng (Δ) đi qua M(0; 1; 2) và có một vectơ chỉ phương là

Mặt cầu (S) có tâm I(1; 0; -2) và bán kính

Ta có

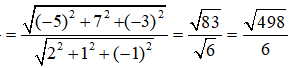
không cắt mặt cầu (S)

Câu 7:

Mặt cầu (S) tâm $I (2; 3; - 1)$ cắt đường thẳng $d : \frac{x - 11}{2} = \frac{y}{1} = \frac{z + 25}{- 2}$ tại 2 điểm A, B sao cho $A B = 16$ có bán kính là:

A. R = 4

B. R = 15

C. R = 16

D. R = 17

Xem đáp án

Chọn D.

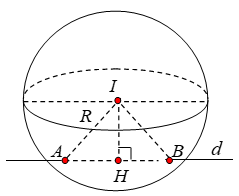
Đường thẳng d đi qua M(11;0;-25) và có vectơ chỉ phương

Gọi H là hình chiếu của I trên (d). Ta có:

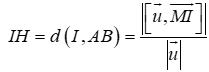
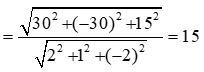
Câu 8:

Viết phương trình tiếp diện của mặt cầu $(S) : x^{2} + y^{2} + z^{2} + 2 x - 4 y - 6 z + 5 = 0$ , biết tiếp diện song song với mặt phẳng $(P) : x + 2 y - 2 z - 1 = 0 .$

A. $x + 2 y - 2 z + 6 = 0 v à x + 2 y - 2 z - 12 = 0$

B. $x + 2 y - 2 z - 6 = 0 v à x + 2 y - 2 z + 12 = 0$

C. $x + 2 y - 2 z + 4 = 0 v à x + 2 y - 2 z - 10 = 0$

D. $x + 2 y - 2 z - 4 = 0 v à x + 2 y - 2 z + 10 = 0$

Xem đáp án

Chọn B.

Mặt cầu (S) tâm I(-1;2;3) và

Do mặt phẳng (α)//(P) nên (α) có dạng : x + 2y - 2z + m = 0.

Do (α) tiếp xúc với (S) ⇔ d(I,(α)) = R.

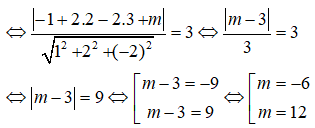
* Với m = - 6 suy ra mặt phẳng có phương trình: x + 2y - 2z - 6 = 0.

* Với m = 12 suy ra mặt phẳng có phương trình: x + 2y - 2z + 12 = 0.

Bắt đầu thi ngay