Bài tập Số phức cơ bản, nâng cao có lời giải (P3)
-
5000 lượt thi
-
25 câu hỏi
-
50 phút
Danh sách câu hỏi
Câu 1:
Cho các số phức w,z thỏa mãn và 5w=(2+i)(z-4).
Giá trị lớn nhất của biểu thức bằng
 Xem đáp án
Xem đáp án
Đáp án C
HD: Ta có
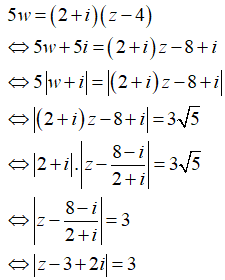
![]() Tập hợp điểm M(z) là đường tròn
Tập hợp điểm M(z) là đường tròn ![]() tâm I(3;-2), R=3.
tâm I(3;-2), R=3.
Gọi A(1;2), B(5;2) và E(3;2) là trung điểm của AB suy ra P=MA+MB
Lại có
![]()
![]() P lớn nhất
P lớn nhất 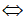 ME lớn nhất.
ME lớn nhất.
Mà ![]()
Vậy ![]()
Câu 2:
Cho số phức z=2+4i. Tính hiệu phần thực và phần ảo của z.
 Xem đáp án
Xem đáp án
Đáp án C.
z=2+4i có phần thực a=2 và phần ảo a=4 nên a-b= 2-4 = -2
Câu 3:
Cho biết có hai số phức z thỏa mãn , kí hiệu là và .
Tính .
 Xem đáp án
Xem đáp án
Đáp án D.
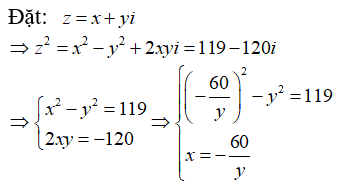
Giải hệ ta tìm được
Câu 4:
Cho w là số phức thay đổi thỏa mãn .
Trong mặt phẳng phức, các điểm biểu diễn số phức z=3w+1-2i chạy trên đường nào?
 Xem đáp án
Xem đáp án
Đáp án A
Ta có: 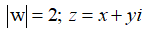
Xét:
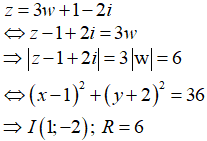
Câu 5:
Cho ba số phức thỏa mãn
Tính giá trị của biểu thức .
 Xem đáp án
Xem đáp án
Đáp án D
Cách 1: Đại số
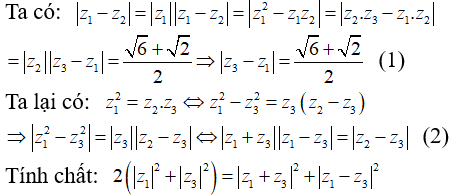
Từ (1) ![]() .
.
Thế vào (2) ta được: 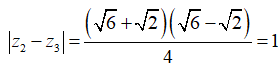 (3)
(3)
Từ (1) và (3): ![]() .
.
Cách 2: Hình học
Ta có:
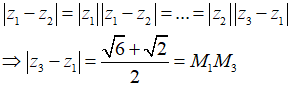 (1)
(1)
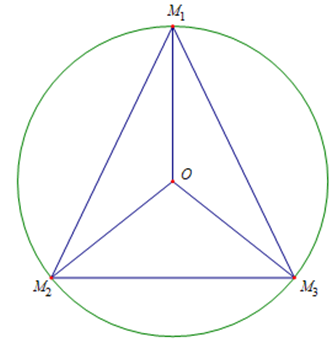
Gọi là 3 điểm biểu diễn
Dễ dàng có:
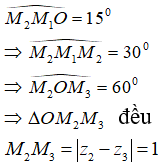 (2)
(2)
Từ (1) và (2):
![]()
Cách 3: Chuẩn hóa chọn .
Câu 7:
Điểm M trong hình vẽ dưới đây biểu thị cho số phức
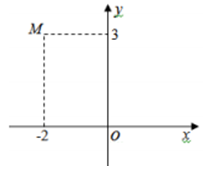
 Xem đáp án
Xem đáp án
Đáp án B
Dựa vào hình vẽ ta thấy M biểu thị cho số phức -2+3i
Câu 8:
Cho là hai nghiệm phức của phương trình (trong đó số phức có phần ảo âm). Tính .
 Xem đáp án
Xem đáp án
Đáp án A
Hai nghiệm của phương trình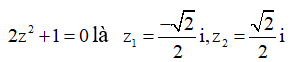 (do có phần ảo âm).
(do có phần ảo âm).
Vậy ![]()
Câu 9:
Có bao nhiêu số phức thỏa mãn
 Xem đáp án
Xem đáp án
Đáp án A
Đăt ![]()
Thay vào biểu thức của bài toán ta có:
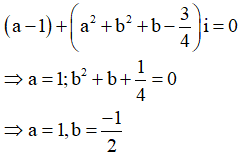
Vậy chỉ có đúng một số phức thỏa mãn bài toán
Câu 10:
Cho số phức z=1+i. Biết rằng tồn tại các số phức
(trong đó ) thỏa mãn .
Tính b-a.
 Xem đáp án
Xem đáp án
Đáp án D
Đặt ![]() lần lượt là các điểm biểu thị cho các số phức
lần lượt là các điểm biểu thị cho các số phức
Vậy ![]()
Từ giả thiết cho ta tam giác MNP cân tại M có ![]()
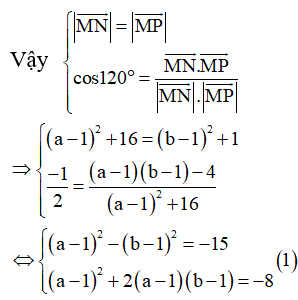
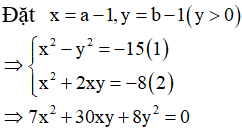
(nhân chéo vế với vế của hai phương trình).
Tìm được  Thay vào (1) thì thấy chỉ có
Thay vào (1) thì thấy chỉ có  thỏa mãn. Lúc này do
thỏa mãn. Lúc này do ![]()
Do 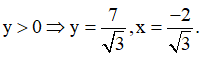
Vậy ![]()
Câu 13:
Có bao nhiêu số phức z thỏa mãn đồng thời hai điều kiện sau: và ?
 Xem đáp án
Xem đáp án
Đáp án B
Gọi M(x;y) biểu diễn cho z, ta có hệ
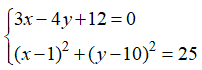
Để ý đường thẳng ![]() tiếp xúc với đường tròn
tiếp xúc với đường tròn ![]() , nên chỉ có một số phức.
, nên chỉ có một số phức.
Câu 14:
Cho số phức z thỏa điều kiện .
Giá trị nhỏ nhất của biểu thức được viết dưới dạng với a, b là các hữu tỉ.
Giá trị của a + b là
 Xem đáp án
Xem đáp án
Đáp án D
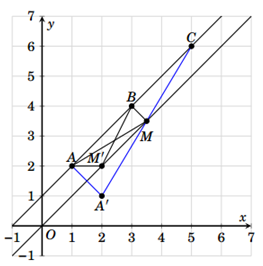
Cách 1
· Đặt ![]() biểu diễn cho số phức z.
biểu diễn cho số phức z.
· Từ giả thiết, ta có M thuộc đường trung trực ![]() của đoạn EF và P=AM+BM+CM
của đoạn EF và P=AM+BM+CM
· Ta chứng minh điểm M chính là hình chiếu vuông góc của B lên đường thẳng .
- Với M’ tùy ý thuộc, M’ khác M. Gọi A’ là điểm đối xứng của A qua . Nhận thấy rằng ba điểm A’, M, C thẳng hàng.
- Ta có ![]()
Mà ![]()
Lại có ![]() Do đó
Do đó ![]()
Cách 2
· Gọi ![]() Từ giả thiết
Từ giả thiết ![]() , dẫn đến y=x .
, dẫn đến y=x .
Khi đó z=x+xi.
· ![]()
· Sử dụng bất đẳng thức ![]()
Dấu đẳng thức xảy ra khi và chỉ khi  . Ta có
. Ta có
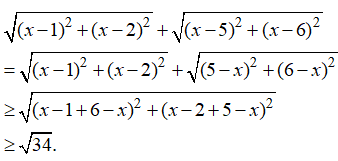
Dấu đẳng thức xảy ra khi và chỉ khi ![]()
· Mặt khác

Dấu đẳng thức xảy ra khi và chỉ khi x=
· Từ hai trường hợp trên, ta thấy, giá trị nhỏ nhất của P là 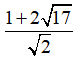 .
.
Khi đó a+b=3.
Câu 15:
Gọi là bốn nghiệm phân biệt của phương trình trên tập số phức.
Tính giá trị của biểu thức
 Xem đáp án
Xem đáp án
Đáp án A
Đặt 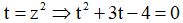
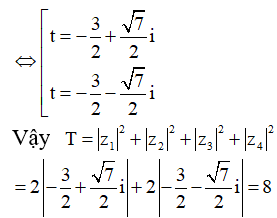
Câu 17:
Cho các số phức z, w thỏa mãn
Tìm giá trị lớn nhất của biểu thức
 Xem đáp án
Xem đáp án
Đáp án D
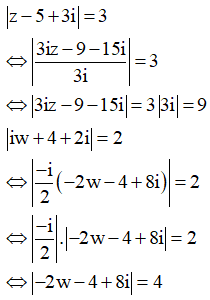
Gọi A và B lần lượt là điểm biểu diễn của 3iz và -2w
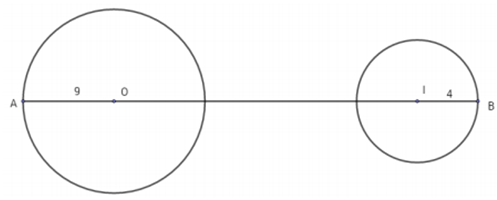
![]() A, B lần lượt thuộc các đường tròn tâm O(9;15) bán kính bằng 9 và đường tròn tâm I(4;-8) bán kính bằng 4
A, B lần lượt thuộc các đường tròn tâm O(9;15) bán kính bằng 9 và đường tròn tâm I(4;-8) bán kính bằng 4
![]() OI=
OI=
Khi đó ![]()
Yêu cầu bài toán trở thành tìm
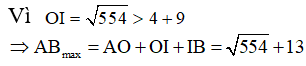
Câu 18:
Cho số phức z thỏa mãn . Biết tập hợp các điểm biểu diễn số phức w xác định bởi là một đường tròn bán kính R. Tính R
 Xem đáp án
Xem đáp án
Đáp án D
![]()
Ta có:
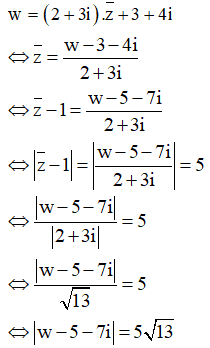
Dễ thấy tập hợp điểm biểu diễn số phức w là đường tròn tâm (5;7) bán kính
Câu 19:
Trong mặt phẳng Oxy, cho các điểm A, B như hình vẽ bên. Trung điểm của đoạn thẳng AB biểu diễn số phức
 Xem đáp án
Xem đáp án
Đáp án B
Phương pháp:
+ Số phức ![]() được biểu diễn bởi điểm M(a;b) trên mặt phẳng xOy.
được biểu diễn bởi điểm M(a;b) trên mặt phẳng xOy.
+ Tọa độ trung điểm I của AB là:
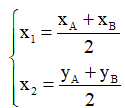
Cách giải:
Dựa vào hình vẽ ta thấy:
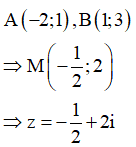
Câu 20:
Gọi là các nghiệm phức của phương trình .
Giá trị của bằng
 Xem đáp án
Xem đáp án
Đáp án A
Phương pháp:
+) Giải phương trình bậc hai ẩn z trên tập số phức.
+) Cho số phức ![]()
Cách giải:
Ta có:
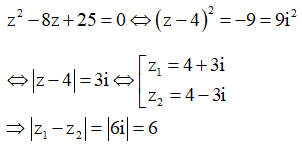
Câu 21:
Có bao nhiêu số phức z thỏa mãn điều kiện ?
 Xem đáp án
Xem đáp án
Đáp án C
Phương pháp:
Gọi z=x+yi thay vào giải thiết và so sánh hai số phức
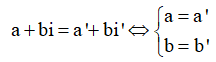
Cách giải:

Do đó có 3 số phức z thỏa mãn bài toán.
Câu 22:
Giả sử là hai trong số các số phức z thỏa mãn và . Giá trị lớn nhất của ![]() bằng
bằng
 Xem đáp án
Xem đáp án
Đáp án D
Phương pháp:
+) Từ giả thiết ![]() , tìm ra đường biểu diễn (C) của các số phức z.
, tìm ra đường biểu diễn (C) của các số phức z.
+) Gọi A, B lần lượt là điểm biểu diễn của ![]()
![]() vị trí của AB đối với đường tròn (C).
vị trí của AB đối với đường tròn (C).
![]()
+) Sử dụng công thức trung tuyến tính
+) Sử dụng BĐT Bunhiascopsky tìm GTLN của OA+OB
Cách giải:
Ta có: ![]()
với ![]()
![]()
![]() M(x;y) biểu diễn z thuộc đường tròn tâm I()bán kính R=1.
M(x;y) biểu diễn z thuộc đường tròn tâm I()bán kính R=1.
Lại có: ![]()
Mặt khác theo công thức trung tuyến ta có:
![]()
Theo BĐT Bunhiascopsky ta có:
![]()
Câu 23:
Điểm nào trong hình vẽ dưới đây là điểm biễu diễn của số phức ?

 Xem đáp án
Xem đáp án
Đáp án D
Ta có ![]()
![]() số phức z biểu diễn Q(3;1)
số phức z biểu diễn Q(3;1)
Câu 24:
Cho số phức z, biết rằng các điểm biễu diễn hình học của các số phức z, iz và z+iz tạo thành một tam giác có diện tích bằng 18. Modun của số phức bằng
 Xem đáp án
Xem đáp án
Đáp án C
Câu 25:
Tập hợp tất cả các điểm biễu diễn các số phức z thõa mãn là đường tròn có tâm I và bán kính R lần lượt là
 Xem đáp án
Xem đáp án
Đáp án A
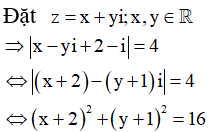
Tập hợp tất cả các điểm biễu diễn các số phức z thỏa mãn ![]() là đường tròn có tâm I và bán kính R lần lượt là
là đường tròn có tâm I và bán kính R lần lượt là ![]()
