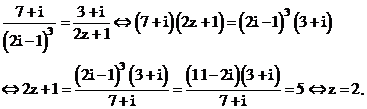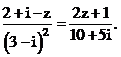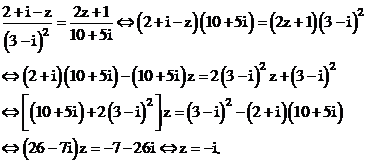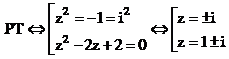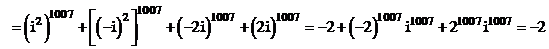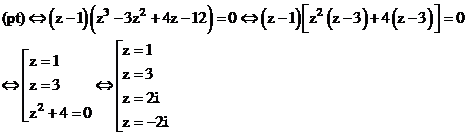Trắc nghiệm Toán 12: Chủ đề 6. Phương trình số phức có đáp án
-
392 lượt thi
-
64 câu hỏi
-
90 phút
Danh sách câu hỏi
Câu 4:
 Xem đáp án
Xem đáp án
Với điều kiện trên, phương trình đã cho trở thành:
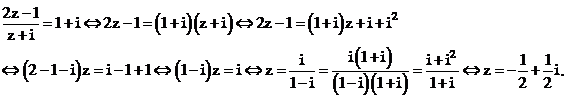
Vậy z cần tìm là:
Vậy chọn đáp án D.
Câu 5:
Tìm nghiệm của phương trình ![]()
 Xem đáp án
Xem đáp án
Với điều kiện trên, phương trình đã cho trở thành:
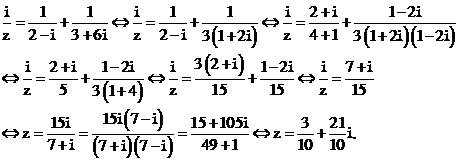
Vậy chọn đáp án C.
Câu 6:
 Xem đáp án
Xem đáp án
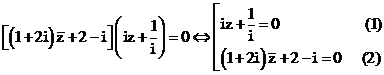
Giải (1):
Giải (2):
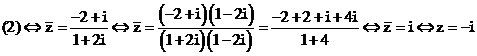
Vậy phương trình có 2 nghiệm là z = i và z = -i.
Vậy chọn đáp án C.
Câu 9:
 Xem đáp án
Xem đáp án
Nên
Vậy chọn đáp án A.
Câu 11:
 Xem đáp án
Xem đáp án
Vậy chọn đáp án A.
Câu 12:
Tìm nghiệm của phương trình ![]() .
.
 Xem đáp án
Xem đáp án
Ta có: ![]() . Phương trình đã cho có hai nghiệm là:
. Phương trình đã cho có hai nghiệm là:
![]()
Vậy chọn đáp án B.
Câu 13:
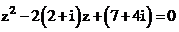 .
. Xem đáp án
Xem đáp án
Vậy phương trình đã cho có hai nghiệm là:
Câu 14:
 Xem đáp án
Xem đáp án
Ta có:
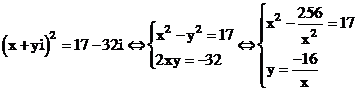

Từ đó, phương trình có hai nghiệm phức là:
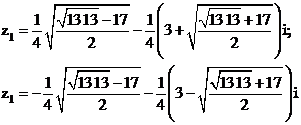
Vậy chọn đáp án A.
Câu 16:
 Xem đáp án
Xem đáp án
Vậy phương trình đã cho có hai nghiệm
Câu 17:
 Xem đáp án
Xem đáp án
Vậy phương trình đã cho có hai nghiệm:
Vậy chọn đáp án B.
Câu 18:
 Xem đáp án
Xem đáp án
Vậy phương trình đã cho có hai nghiệm:
Vậy chọn đáp án D.
Câu 19:
 Xem đáp án
Xem đáp án
Vậy phương trình đã cho có hai nghiệm:
Vậy chọn đáp án C.
Câu 20:
 Xem đáp án
Xem đáp án
Ta có
Suy ra
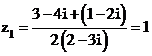
và
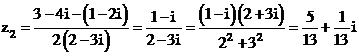
vậy phương trình có hai nghiệm là
Vậy chọn đáp án D.
Câu 21:
 Xem đáp án
Xem đáp án
Nên
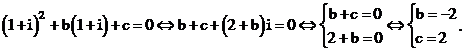
Vậy,
Vậy chọn đáp án D.
Câu 22:
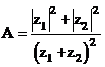 .
. Xem đáp án
Xem đáp án
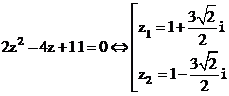
Lúc đó:
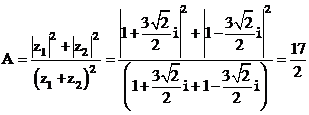 .
.Vậy chọn đáp án B.
Câu 23:
 Xem đáp án
Xem đáp án
Phương trình có hai nghiệm là:
Vậy
Vậy chọn đáp án C.
Câu 24:
 Xem đáp án
Xem đáp án
Do đó phương trình có hai nghiệm là
Vậy chọn đáp án D.
Câu 25:
 Xem đáp án
Xem đáp án
Phương trình đã cho có hai nghiệm là 1 + 4i và 1 - 4i.
Nếu z1 = 1 + 4i thì
Nếu z1 = 1 -4i thì
Vậy chọn đáp án D.
Câu 26:
 Xem đáp án
Xem đáp án
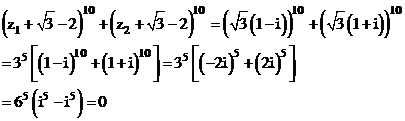
Vậy chọn đáp án B.
Câu 27:
 Xem đáp án
Xem đáp án
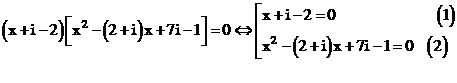
Giải (1): x = 2 - i
Giải (2):
Vậy phương trình (2) có hai nghiệm phân biệt là:
Câu 28:
29.1. Tính
 Xem đáp án
Xem đáp án
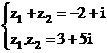
Do đó:
Chọn đáp án C
Câu 32:
 Xem đáp án
Xem đáp án
Phương trình có hai nghiệm
Vậy
Câu 33:
 Xem đáp án
Xem đáp án
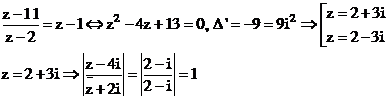
Vậy chọn đáp án A
Câu 34:
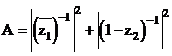 . Tìm giá trị của biểu thức
. Tìm giá trị của biểu thức Xem đáp án
Xem đáp án
Phương trình đã cho tương đương với: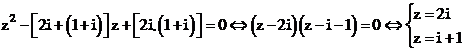
Do ![]() nên ta có z1 = 2i và z2 = i + 1
nên ta có z1 = 2i và z2 = i + 1
Ta có 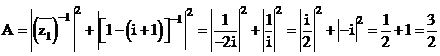
Chọn đáp án B
Câu 35:
Gọi z1, z2 lần lượt là hai nghiệm của phương trình ![]() . Tính giá trị của biểu thức
. Tính giá trị của biểu thức![]()
 Xem đáp án
Xem đáp án
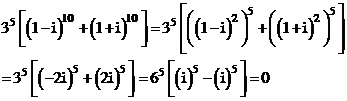
Từ đó ta có lời giải như sau:
Phương trình đã cho tương đương với:
Do Q là biểu thức đối xứng với z1, z2 nên không mất tính tổng quát, giả sử
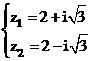
Lúc đó:
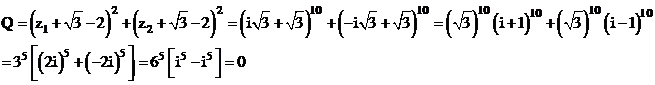
Vậy chọn đáp án C.
Câu 36:
 Xem đáp án
Xem đáp án
Với z = 3 + 2i ta có
Vậy chọn đáp án B.
Câu 37:
 Xem đáp án
Xem đáp án
Phương trình đã cho có hai nghiệm
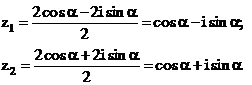
Vậy chọn đáp án A.
Câu 38:
 Xem đáp án
Xem đáp án
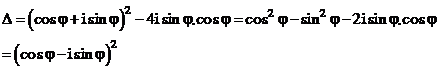
Do đó, phương trình đã cho có hai nghiệm
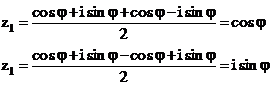
Vậy chọn đáp án B.
Câu 39:
 Xem đáp án
Xem đáp án
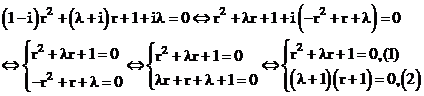
Từ phương trình (2) ta có:
- Nếu
- Nếu
Vậy phương trình đã cho không có nghiệm thực khi và chỉ khi
Vậy chọn đáp án C.
Câu 40:
40.1. Tìm giá trị lớn nhất của
 Xem đáp án
Xem đáp án
Do đó:
Từ
32.1. Giá trị lớn nhất của khi khi đó:
Câu 41:
 Xem đáp án
Xem đáp án
32.2. Giá trị nhỏ nhất của khi khi đó:
![]() Vậy chọn đáp án B.
Vậy chọn đáp án B.
Câu 42:
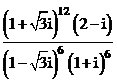 là nghiệm của phương trình
là nghiệm của phương trình  Xem đáp án
Xem đáp án
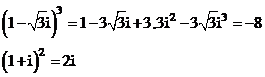
Do đó
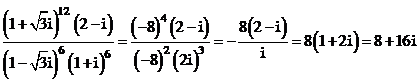
Theo giả thiết ta có
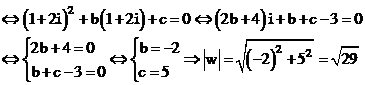
Vậy chọn đáp án C.
Câu 43:
 Xem đáp án
Xem đáp án
Bởi vì
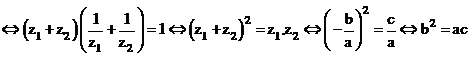
Vậy chọn đáp án D.
Câu 44:
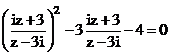 .
. Xem đáp án
Xem đáp án
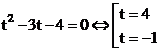
Với
Với
Vậy chọn đáp án C.
Câu 45:
 Xem đáp án
Xem đáp án
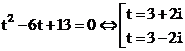
Với
Với
Vậy chọn đáp án D.
Câu 46:
 Xem đáp án
Xem đáp án
Giải (2): ta có
Suy ra
Do đó:
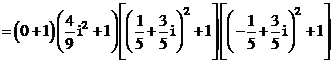
Vậy chọn đáp án B.
Câu 47:
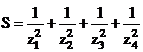 .
. Xem đáp án
Xem đáp án
Thay vào biểu thức
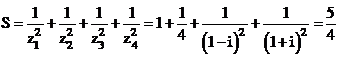
Vậy chọn đáp án C.
Câu 49:
 Xem đáp án
Xem đáp án
Vậy phương trình nhận z = 1 là nghiệm.
Phương trình
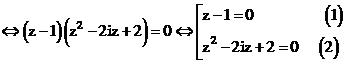
Giải (1):
Giải (2): Ta có
Phương trình (2) có 2 nghiệm là
Vậy phương trình đã cho có 3 nghiệm là:
Vậy chọn đáp án D.
Câu 50:
 Xem đáp án
Xem đáp án
Phương trình
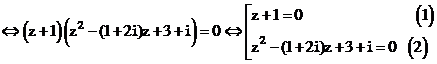
Giải (1):
Giải (2):
Phương trình (2) có hai nghiệm là:
Kết luận:
Vậy chọn đáp án D.
Câu 51:
Tính
 Xem đáp án
Xem đáp án
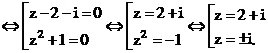
Vậy phương trình có 3 nghiệm là:
Vậy chọn đáp án B.
Câu 52:
 Xem đáp án
Xem đáp án
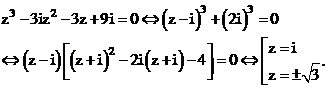
Vậy nghiệm của phương trình là:
Vậy chọn đáp án B.
Câu 53:
 Xem đáp án
Xem đáp án
Chia đa thức
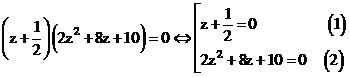
Giải (1):
Giải (2):
Do đó, phương trình (2) có hai nghiệm là:
Vậy phương trình có 3 nghiệm là:
Vậy chọn đáp án D.
Câu 54:
 Xem đáp án
Xem đáp án
Chia đa thức
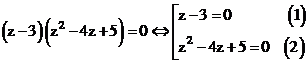
Giải (1):
Giải (2): Ta có:
Do đó phương trình (2) có hai nghiệm:
Vậy phương trình có 3 nghiệm là:
Câu 55:
 Xem đáp án
Xem đáp án
Suy ra
Do đó phương trình phải có dạng:
Chia đa thức
Vậy phương trình đã cho có 3 nghiệm là:
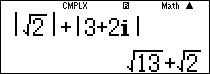
Vậy chọn đáp án D.
Câu 56:
 Xem đáp án
Xem đáp án
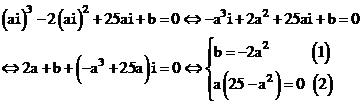
Ta có:
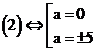
Với
Với
Vậy chọn đáp án C.
Câu 57:
 Xem đáp án
Xem đáp án
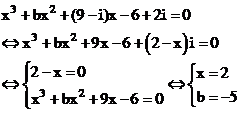
Suy ra phương trình có dạng:
với z = 2 là nghiệm thực của phương trình.
Chia đa thức
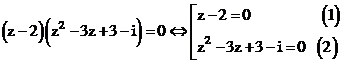
Giải (1):
Giải (2): Ta có:
Câu 58:
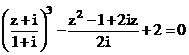
 Xem đáp án
Xem đáp án
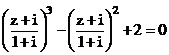 .
.Đặt
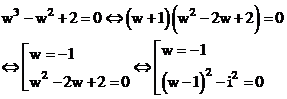 .
.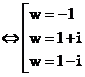
- Với w = -1:
- Với w = 1+i:
- Với w= 2 - i:
Vậy phương trình có 3 nghiệm:
Vậy chọn đáp án C.
Câu 59:
 Xem đáp án
Xem đáp án
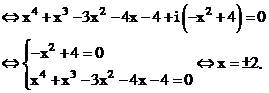
Như vậy phương trình được biến đổi thành phương trình tích có dạng:
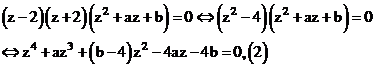
Đồng nhất phương trình (1) và (2) ta được:
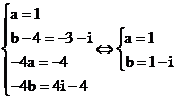
Vậy phương trình (1) tương đương với:
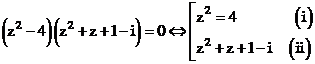
Giải (i):
Giải (ii): Ta có:
Vậy phương trình đã cho có 4 nghiệm:
Vậy chọn đáp án A.
Câu 60:
 Xem đáp án
Xem đáp án
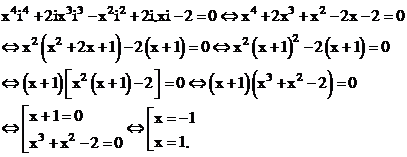
Vậy 2 nghiệm thuần ảo của phương trình là
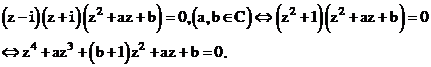
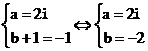
Phương trình trở thành:
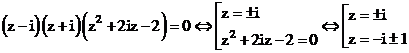
Kết luận: Phương trình đã cho có 4 nghiệm là:
Suy ra:
Câu 61:
 Xem đáp án
Xem đáp án
Ta có A + B + C + D + E = 0 Suy ra phương trình có 1 nghiệm: z = 1.
Chia đa thức cho
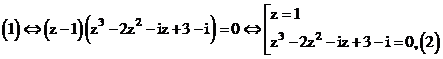
Phương trình (2) lại có các hệ số thỏa mãn:
Do đó phương trình (2) có 1 nghiệm z = -1.
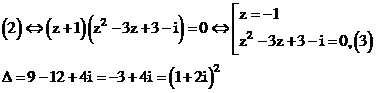
Suy ra (3) có 2 nghiệm là
Kết luận: Phương trình (1) có 4 nghiệm là:
Câu 62:
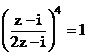 . Tính giá trị của biểu thức:
. Tính giá trị của biểu thức:  Xem đáp án
Xem đáp án
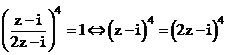
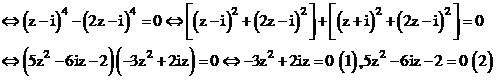
Giải (2) ta có
Suy ra
Do đó
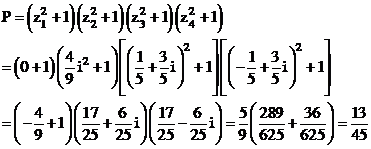
Vậy chọn đáp án B.
Câu 63:
Tìm
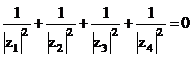 .
. Xem đáp án
Xem đáp án
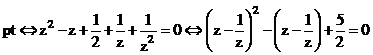
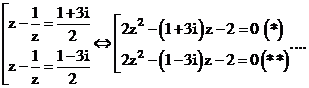
Giải (*) {Kĩ thuật MTCT}
Ghi vào màn hình:
Ta được nghiệm của phương trình:
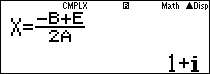
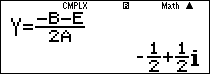
Chỉ cần thay đổi các hệ số của phương trình ta tìm được nghiệm của phương trình (2)
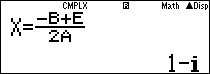
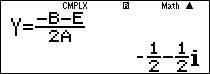
Suy ra:
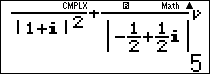
Vậy chọn đáp án A.

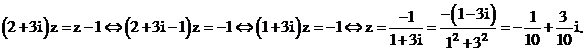
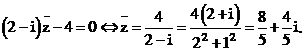
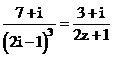 .
.